
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к решению первойСодержание книги
Поиск на нашем сайте
КОНТРОЛЬНОЙ РАБОТЫ В этом параграфе приведён разбор решений задач типового варианта контрольной работы по математическому анализу. ЗАДАЧА 1. Вычислить пределы функций а) —д): а) 1. ► 2. ► 3. ► б) Решение.
Предел
 не может быть вычислен подстановкой не может быть вычислен подстановкой  , поскольку в результате подстановки получается неопределенность , поскольку в результате подстановки получается неопределенность  . .
в) Анализ задачи. Подстановка числа 2 вместо Решение. Выражение Другое решение задачи. Воспользуемся правилом Лопиталя
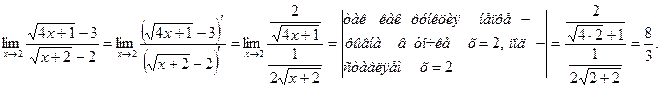
Анализ задачи. В данном случае, непосредственное применение теоремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаменатели равны пулю.
Таким образом, рассматриваемый предел представляет собой неопределённость вида Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если =
Отсюда,
Аналогично, Поэтому, Преобразуем выражение находящиеся под знаком предела:
= Другое решение задачи. Поскольку пределы числителя и знаменателя при Равны нулю, применимо правило Лопиталя.
д) Анализ задачи. Подстановка числа 0 вместо x показывает, что пределы числителя и знаменателя при Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения, либо применить правило Лопиталя. Решение. Совершим замену неизвестной
Так как
Используем теперь тригонометрическую формулу
Другое решение. Воспользуемся вновь правилом Лопиталя
ЗАДАЧА 2. Вычислить производные функций а) – в): а) Вычислить производную функции
► б) Вычислить производную функции 1. ►
в) Вычислить производную функции
► 2. ►
3. ►
ЗАДАЧА 3. Исследовать функцию и построить график Исследовать функцию ►Исследуем данную функцию. 1. Областью определения функции является множество 2. Ордината точки графика 3. Точки пересечения графика данной функции с осями координат: 4. Легко находим, что
Находим наклонные асимптоты:
Таким образом, существует единственная наклонная асимптота
5. Исследуем функцию на возрастание, убывание, локальный экстремум:' y= 2(х + 3)(x-4)-(x + 3)2 _ 2x2 – 2x - 24 – х2 - 6х - 9 = = Из у' = 0 следует хг — 8х — 33 = 0, откуда у' < 0, следовательно, функция убывает на этом интервале; в (11; +∞) у'>0, т. е. функции возрастает. В точке 6. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем
= Очевидно, что в интервале (—∞; 4) y"< 0, и в этом интервале кривая выпукла; в (4; +∞) у" > 0, т. е. в этом интервале кривая вогнута. Так как при х = 4 функция не определена, то точка перегиба отсутствует. 7. График функции изображен на рис. 0.17
ЗАДАЧА 4. Вычислить неопределенные интегралы а) – в) а) 1. ► 2. ►
3. ►
4. ►
б) Решение. Решение данной задачи на формуле интегрирования по частям:
В этой формуле принимаем за
Подставляя найденные
в) Решение. Так как корнями знаменателя является
Подставим дробь в виде следующей суммы:
и найдем коэффициенты А и В. Приведем дроби в правой равенства части к общему знаменателю:
Приравняв числители, получим (2) Подставив в последнее равенство
Подставляя
Таким образом, Итак, Здесь мы воспользуемся формулой (1)
ЗАДАЧА 5. Вычислите площадь фигуры, ограниченной графиками функций Решение. Графиком функции
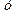

Найдем точки пересечения графиков функции:
Заметим, что Пусть

Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида (3) где Для решения уравнения такого вида необходимо сделать следующее: 1). Разделить переменные, т. е. Преобразовать уравнение к виду (4) 2). Проинтегрировать обе части уравнения (4)
(5) где 3). Разрешить, если это возможно, уравнение (5) относительно y (и найти область определения решения): 4). Добавить к решению (5) все функции вида
Описанный метод решения можно схематично представить в виде формулы:
ЗАДАЧА 6. Найти общее решение дифференциального уравнения Решение. 1). Преобразуем уравнение к виду
у2 + х2 = R2.
D(у) = 4). В данном случае, уравнение y = а нет.
Линейные дифференциальные уравнение второго порядка с постоянными коэффициентами. Уравнение вида (7) у" + by' + су=0, где b и с — некоторые числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Общее решение
. (8) k 2 + bk + c = 0 имеют следующий вид: A) Б) где α— единственный корень характеристического уравнения; B) где Общее решение (9) является суммой некоторого его частного решения
Многочлен В тех случаях, когда
1.
2. если
3.
Задача 7. Найти частное решение дифференциального уравнения Решение. 1). Характеристического уравнение: Так как D = — 16, используем формулу В):
2). Так как правая часть
Подставляя у =
Сравнивая коэффициенты при одинаковых степенях х, находим:
Отсюда 3). Находим частное решение, удовлетворяющее начальным условиям, данным в задаче:
Напомним, что число n! (читается «эн-факториал»)- это произведение всех натуральных чисел от единицы до
При вычислениях с факториалами представляется важным следующее соображение:
Признак Даламбера. Если существует предел То числовой ряд ЗАДАЧА 8. Исследовать сходимость ряда
Решение:
Вычисляем предел
Контрольная работа № 1 Формулировки условий задач контрольной работы. [1]. Вычислить предел функции. [2]. Вычислить производную функцию. [3]. Исследовать функцию, построить график. [4]. Вычислить неопределённые интегралы. [5] Вычислить площадь фигуры, ограниченной графиками функций f(x) и [6]. Найти общее решение дифференциального уравнения и построить графики двух ►Вариант 0◄ 1. а) в) д) 2. а) в) 3. 4. а) в) 5. 6. 7. 8. ►Вариант 1◄ 1. а) в) д) 2. а) в) 3. 4. а) в)
5.
6.
7.
8.
►Вариант 2◄
1. а) в) д) 2. а) в)
3.
4. а) в)
5.
6.
7.
8. ►Вариант 3◄ 1. а) в) д) 2. а) в) 3. 4. а) в)
5.
6.
7.
8.
►Вариант 4◄
1. а) в) д)
2. а) в) 3.
4. а) в)
5. 6. 7. 8.
►Вариант 5◄ 1. а) в) д)
2. а) в)
3.
4. а) в) 5. 6. 7. 8. ►Вариант 6◄
1. а) в) д)
2. а) в)
3.
4. а) в)
5.
6.
7.
8. ►Вариант 7◄ 1. а) в) д) 2. а) в) 3. 4. а) в) 5. 6. 7. 8. ►Вариант 8◄
1. а) в) д) 2. а) в) 3. 4. а) в) 5. 6. 7. 8. ►Вариант 9◄
1. а) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 .
. =
=  .
. .
.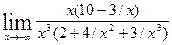 =
= 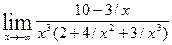 =
=  =0.◄
=0.◄ ..
..
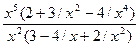 =
=  =-∞.
=-∞. .
. =
= 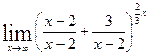 =
=  =
= 

 =
=  =
=  =
=
 вычислен подстановкой
вычислен подстановкой 
 .
.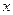 показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность
показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность  . Для этого можно либо провести тождественные преобразования выражения
. Для этого можно либо провести тождественные преобразования выражения  , либо применить правило Лопиталя.
, либо применить правило Лопиталя. является сопряженным по отношению к выражению
является сопряженным по отношению к выражению  , а выражение
, а выражение  - по отношению к
- по отношению к  . Умножая числитель и знаменатель дроби на произведение сопряженных выражений (
. Умножая числитель и знаменатель дроби на произведение сопряженных выражений ( , получаем
, получаем 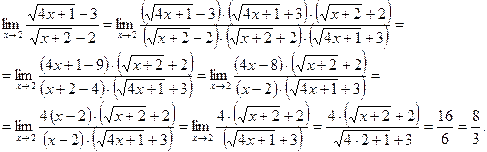

 и
и 
 — корни квадратного трехчлена
— корни квадратного трехчлена 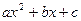 , то
, то  Решаем квадратное уравнение, находя его дискриминант D.
Решаем квадратное уравнение, находя его дискриминант D.

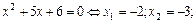

 =
=  =
=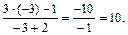


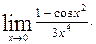
 равны нулю. Поэтому, имеет место неопределённость
равны нулю. Поэтому, имеет место неопределённость 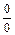 .
.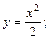 при этом
при этом 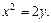

 при
при  то
то 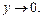

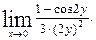



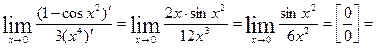

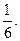

 ◄
◄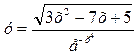 .
.
 ◄
◄ .
. .◄
.◄ .
.
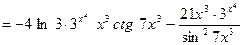 .◄
.◄

 .◄
.◄ и построить её график.
и построить её график. .
. .
.

 .
.

 .
.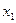 = 11, х2= — 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у(—3) = 0. В интервале (4; 11)
= 11, х2= — 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у(—3) = 0. В интервале (4; 11) =
= =
=  .
.

 ◄
◄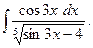

 ◄
◄

 .◄
.◄

 .◄
.◄ .
.
 По формуле
По формуле 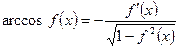 находим производственную второго сомножителя
находим производственную второго сомножителя 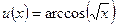 :
:
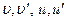 в формулу интегрирования по частям получаем:
в формулу интегрирования по частям получаем: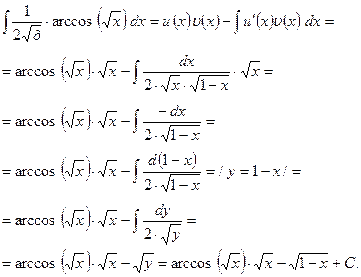
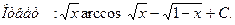
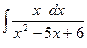 )
) , то по формуле
, то по формуле  , знаменатель раскладываются на множители
, знаменатель раскладываются на множители .
. ,
,
 .
. , находим, что
, находим, что
 в равенство (2), находим, что
в равенство (2), находим, что
 .
.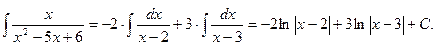

 . Изобразите эту фигуру на координатной плоскости.
. Изобразите эту фигуру на координатной плоскости. является парабола, ветви которой направлены вверх. Вычисляем производную функции
является парабола, ветви которой направлены вверх. Вычисляем производную функции  и находим координаты вершины параболы С:
и находим координаты вершины параболы С:


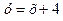





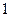




 Рис. к задаче 5
Рис. к задаче 5 .
.
 Графиком функции
Графиком функции  является прямая, которую можно построить по двум точкам
является прямая, которую можно построить по двум точкам  .
. площадь фигуры
площадь фигуры  , ограниченной графиками функций. Так как
, ограниченной графиками функций. Так как 




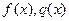 - заданные функции называются дифференциальным уравнением с разделяющимися переменными.
- заданные функции называются дифференциальным уравнением с разделяющимися переменными. .
.
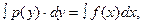

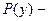 первообразная функции
первообразная функции  первообразная функции
первообразная функции  произвольная постоянная.
произвольная постоянная.
 (горизонтальные прямые), где число
(горизонтальные прямые), где число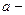 один из корней уравнения
один из корней уравнения 

 Построить графики двух частных решений этого уравнения.
Построить графики двух частных решений этого уравнения.

 Равенство
Равенство 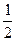 (у2 + х2) = С показывает, что С > 0. Положим С =
(у2 + х2) = С показывает, что С > 0. Положим С = 
 3). Разрешим, предыдущее уравнение относительно у и найдём область определения решения:
3). Разрешим, предыдущее уравнение относительно у и найдём область определения решения: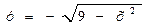 Рис. к задаче 6.
Рис. к задаче 6.
 >0. Графики решений — дуги концентрических окружностей произвольного радиуса с центром в начале координат (см. рис.).
>0. Графики решений — дуги концентрических окружностей произвольного радиуса с центром в начале координат (см. рис.).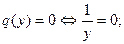 не имеет решений. Поэтому решений вида
не имеет решений. Поэтому решений вида
 этого уравнения в зависимости от знака дискриминанта
этого уравнения в зависимости от знака дискриминанта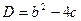 характеристического уравнения
характеристического уравнения если D > 0, где k =α, к= β— два различных действительных корня (α≠β) характеристического уравнения (8);
если D > 0, где k =α, к= β— два различных действительных корня (α≠β) характеристического уравнения (8); , если D = О,
, если D = О, если D < О,
если D < О,
 линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
 и общего решения
и общего решения . однородного уравнения (7), т. е.
. однородного уравнения (7), т. е.
 называют характеристическим многочленом дифференциального уравнения (7).
называют характеристическим многочленом дифференциального уравнения (7). представляет собой многочлен, функцию
представляет собой многочлен, функцию ,частное решение
,частное решение  удаётся найти подбором с помощью следующей таблицы.
удаётся найти подбором с помощью следующей таблицы.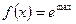 :
: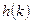
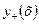


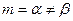
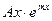
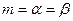
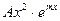
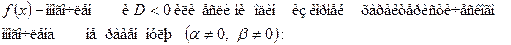

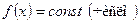
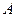

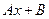
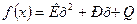
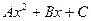
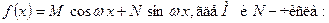
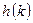

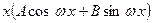
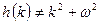

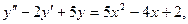 удовлетворяющее начальным условиям у (0) = 1, у' (0) = 2.
удовлетворяющее начальным условиям у (0) = 1, у' (0) = 2.
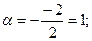
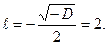 Общее решение однородного уравнения:
Общее решение однородного уравнения: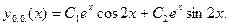
 многочлен второй степени, частное решение неоднородного уравнения будем искать в виде многочлена 2-ой степени с неопределёнными коэффициентами:
многочлен второй степени, частное решение неоднородного уравнения будем искать в виде многочлена 2-ой степени с неопределёнными коэффициентами:
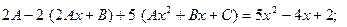


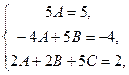
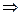
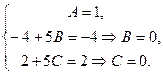
 поэтому общее решение неоднородного уравнения имеет вид
поэтому общее решение неоднородного уравнения имеет вид 

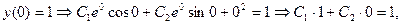
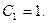
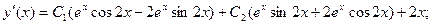

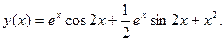
 :
: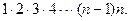

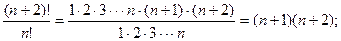
 и т.д.
и т.д.
 сходится при
сходится при  и расходится при
и расходится при 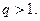

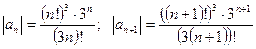 .
.



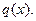
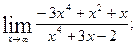 б)
б) 
 г)
г) 

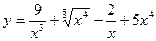 ; б)
; б)  ;
;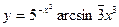
 .
.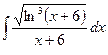 ; б)
; б) 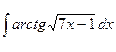 ;
; ;
;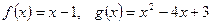 .
.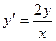 .
. ,
,  .
.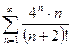 .
. б)
б) 
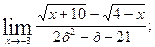 г)
г) 
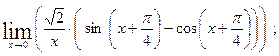
 ; б)
; б) 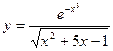 ;
;
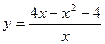 .
.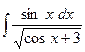 ; б)
; б) 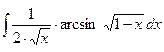 ;
; ;
;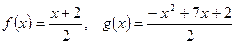 .
. .
.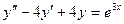 ,
, 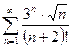 .
.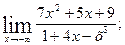 б)
б) 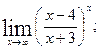
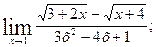 г)
г) 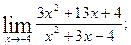
 ;
; ; б)
; б)  ;
;
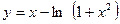 .
.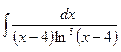 ; б)
; б)  ;
;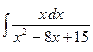 ;
;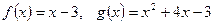 .
.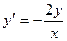 .
. ,
, 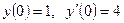 .
.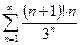 .
. б)
б) 
 г)
г) 
 ; б)
; б)  ;
;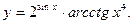
 .
.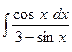 ; б)
; б) 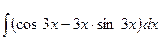 ;
;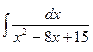 ;
; .
. .
.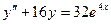 ,
,  .
. .
.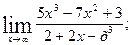 б)
б) 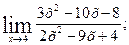 г)
г) 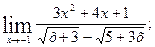
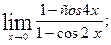
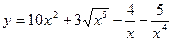 ; б)
; б)  ;
;
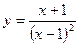 .
. ; б)
; б)  ;
; ;
; .
.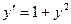 .
.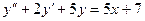 ,
, 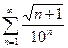 .
. б)
б) 
 г)
г) 

 ; б)
; б) 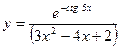 ;
;
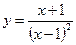 .
.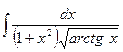 ; б)
; б)  ;
; ;
; .
.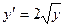 .
.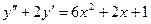 ,
, 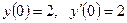 .
.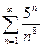 .
.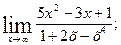 б)
б) 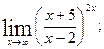
 г)
г) 
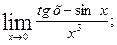
 ; б)
; б) 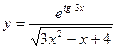 ;
;
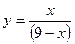 .
. ; б)
; б)  ;
; ;
;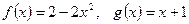 .
.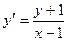 .
.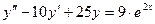 ,
,  .
. .
. б)
б) 
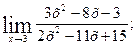 г)
г) 

 ; б)
; б) 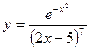 ;
;
 .
.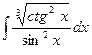 ; б)
; б) 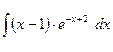 ;
;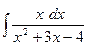 ;
;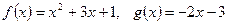 .
.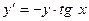 .
. ,
,  .
. .
.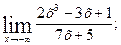 б)
б) 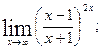
 г)
г) 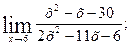
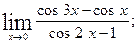
 ; б)
; б)  ;
;
 .
.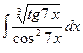 ; б)
; б)  ;
; ;
;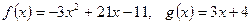 .
. .
. ,
,  .
. .
.


