
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные признаки сходимости рядаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимый признак сходимости не дает, вообще говоря, возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью так называемых достаточных признаков. Рассмотрим некоторые достаточные признаки сходимости числовых рядов с положительными членами.
Признаки сравнения рядов.
Сходимость или расходимость числовых рядов с положительными членами часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы, которые примем без доказательства. Теорема 1.3. Пусть даны два ряда с положительными членами:
и
Если для всех 1) из сходимости ряда (1.9) следует сходимость ряда (1.8); 2) из расходимости ряда (1.8) следует расходимость ряда (1.9).
Надо отметить, что теорема 1.3 справедлива и в том случае, когда неравенство
Теорема 1.4 (предельный признак сравнения). Пусть даны два ряда (1.8) и (1.9) с положительными членами. Если существует конечный, отличный от нуля, предел
где
Пример 1.5. Исследовать на сходимость ряд Решение. Сравним данный ряд с рядом геометрической прогрессии Пример 1.6. Исследовать на сходимость ряд Решение. Здесь Пример 1.7. Исследовать на сходимость ряд Решение. Применим предельный признак сравнения, используя гармонический ряд Признак Даламбера
В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами.
Теорема 1.5 (признак Даламбера). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел
Тогда: 1) при 2) при
При Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида Пример 1.8. Исследовать на сходимость ряд Решение. Применим признак Даламбера:
Находим
Так как Пример 1.9. Исследовать на сходимость ряд Решение. Применим признак Даламбера:
Находим
Так как ,
Радикальный признак Коши
Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости числового ряда с положительными членами. Этот признак во многом схож с признаком Даламбера.
Теорема 1.6 (радикальный признак Коши). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел
Тогда: 1) при 2) при При Пример 1.10. Исследовать на сходимость ряд Решение. Так как
то применим радикальный признак Коши к ряду
Ряд
Интегральный признак Коши
Теорема 1.7 (интегральный признак Коши). Пусть дан ряд
члены которого являются значениями непрерывной положительной функции
и пусть Надо отметить, что вместо интеграла Пример 1.11. Исследовать на сходимость ряд
где Решение. Рассмотрим функцию При
При Таким образом, при , Пример 1.12. Исследовать на сходимость ряд Решение. Воспользуемся интегральным признаком Коши. Рассмотрим функцию
Поскольку несобственный интеграл расходится, то и исходный ряд расходится. , Пример 1.13. Исследовать на сходимость ряд Решение. Воспользуемся интегральным признаком Коши. Рассмотрим функцию Находим
Поскольку несобственный интеграл сходится, то и исходный ряд сходится. , 2. ЗНАКОЧЕРЕДУЮЩИЕСЯ И ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
Знакочередующиеся ряды. Признак Лейбница
Рассмотрим важный класс рядов, у членов которых поочередно изменяются знаки. Такие ряды называются знакочередующиеся. Определение 2.1. Знакочередующимся рядом называется ряд вида
где
Для знакочередующихся рядов имеет место достаточный признак сходимости, установленный в 1714 г. Лейбницем в письме к И.Бернулли. Теорема 2.1 (признак Лейбница). Знакочередующийся ряд (2.1) сходится, если 1) последовательность абсолютных величин ряда монотонно убывает, т.е.
2) общий член ряда стремится к нулю, т.е.
При этом сумма
Следствие. Остаток
Например, по признаку Лейбница ряд
сходится, т.к. выполняются условия теоремы 2.1: 1)
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 754; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.238 (0.006 с.) |

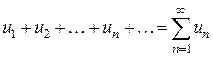 (1.8)
(1.8)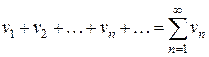 (1.9)
(1.9) выполняется неравенство
выполняется неравенство  , то
, то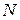 . Это вытекает из свойства 3 числовых рядов.
. Это вытекает из свойства 3 числовых рядов.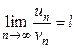
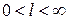 , то ряды (1.8) и (1.9) сходятся или расходятся одновременно.
, то ряды (1.8) и (1.9) сходятся или расходятся одновременно.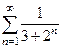 .
. , который сходится, так как
, который сходится, так как  . Имеем
. Имеем  . Следовательно, данный ряд сходится.,
. Следовательно, данный ряд сходится., .
. . Возьмем для сравнения гармонический ряд
. Возьмем для сравнения гармонический ряд  , который расходится. Имеем
, который расходится. Имеем 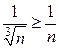 . Следовательно, данный ряд расходится.,
. Следовательно, данный ряд расходится.,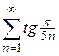 .
.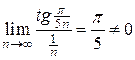 , то данный ряд расходится.,
, то данный ряд расходится.,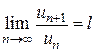 .
.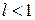 ряд сходится;
ряд сходится;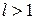 ряд расходится.
ряд расходится.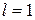 признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.
признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.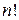 или
или  .
.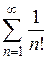 .
. ,
, 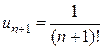 .
.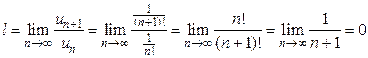 .
.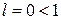 , то данный ряд по признаку Даламбера сходится.,
, то данный ряд по признаку Даламбера сходится., .
.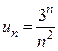 ,
, 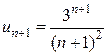 .
.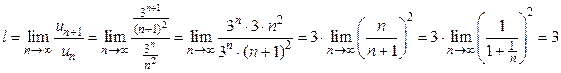 .
.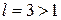 , то данный ряд по признаку Даламбера расходится.
, то данный ряд по признаку Даламбера расходится.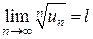 .
.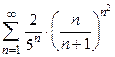 .
. ,
, .
. .
.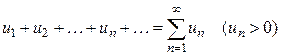 ,
, при целых значениях аргумента
при целых значениях аргумента 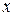 :
: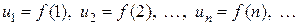 ,
,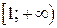 . Тогда ряд сходится, если сходится несобственный интеграл
. Тогда ряд сходится, если сходится несобственный интеграл  , и расходится, если несобственный интеграл
, и расходится, если несобственный интеграл  расходится.
расходится.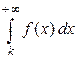 , где
, где 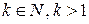 . Отбрасывание
. Отбрасывание 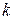 первых членов ряда, как известно, не влияет на сходимость (расходимость) ряда.
первых членов ряда, как известно, не влияет на сходимость (расходимость) ряда.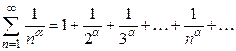 , (1.10)
, (1.10)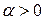 - действительное число, ряд называется обобщенным гармоническим рядом или рядом Дирихле.
- действительное число, ряд называется обобщенным гармоническим рядом или рядом Дирихле.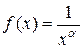 , которая непрерывна и монотонно убывает на промежутке
, которая непрерывна и монотонно убывает на промежутке 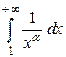 .
.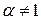 имеем
имеем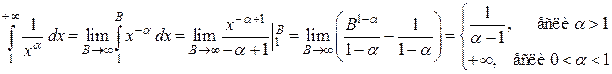 .
. получаем гармонический ряд
получаем гармонический ряд 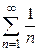 , который расходится.
, который расходится.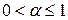 ряд Дирихле расходится, а при
ряд Дирихле расходится, а при 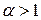 ряд Дирихле сходится.
ряд Дирихле сходится.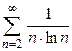 .
.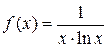 , которая непрерывна и монотонно убывает на промежутке
, которая непрерывна и монотонно убывает на промежутке 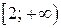 . Находим
. Находим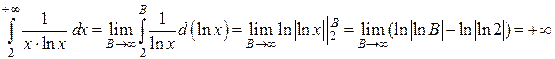 .
.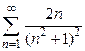 .
. , которая непрерывна и монотонно убывает на промежутке
, которая непрерывна и монотонно убывает на промежутке  .
. , (2.1)
, (2.1)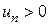 для всех
для всех 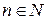 (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
(т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).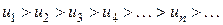 ;
;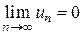 .
.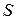 ряда (2.1) удовлетворяет неравенствам
ряда (2.1) удовлетворяет неравенствам 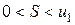 .
.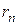 ряда (2.1) по абсолютной величине меньше абсолютной величины первого из отбрасываемых членов, т.е.
ряда (2.1) по абсолютной величине меньше абсолютной величины первого из отбрасываемых членов, т.е.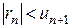 .
.
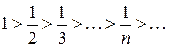 ; 2)
; 2)  .
.


