Отбор информативных признаков
Будем считать, что набор исходных признаков задан. Фактически его определяет учитель. Важно, чтобы в него вошли те признаки, которые действительно несут различительную информацию. Выполнение этого условия в решающей степени зависит от опыта и интуиции учителя, хорошего знания им той предметной области, для которой создаётся система распознавания. Если исходное признаковое пространство задано, то отбор меньшего числа наиболее информативных признаков (формирование признакового пространства меньшей размерности) поддаётся формализации. Пусть  – исходное признаковое пространство, – исходное признаковое пространство,  – преобразованное признаковое пространство, – преобразованное признаковое пространство,  – некоторая функция. – некоторая функция.
На рис. 16 представлено линейное преобразование координат
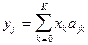 . .
После преобразования признак  не несёт различительной информации и его использование для распознавания не имеет смысла. не несёт различительной информации и его использование для распознавания не имеет смысла.
На рис. 17 проиллюстрирован переход от декартовой системы координат к полярной, что привело к целесообразности отбрасывания признака  . .
Такого рода преобразования приводят к упрощению решающих правил, т.к. их приходится строить в пространстве меньшей размерности. Однако при этом возникает необходимость в реализации преобразования 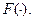 Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование. Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование.
     
          
         
        
        
    
 
   
  
 
     | |    

Рис. 16. Линейное преобразование координат
с последующим отбрасыванием одного из признаков
Особо выделим следующий тип линейного преобразования:
 , ,
где  – диагональная матрица, причём её элементы равны либо 0, либо 1. – диагональная матрица, причём её элементы равны либо 0, либо 1.
Это означает, что из исходной системы признаков часть отбрасывается. Разумеется, остающиеся признаки должны образовывать наиболее информативную подсистему. Таким образом, нужно разумно организовать процедуру отбора по одному из ранее рассмотренных критериев информативности. Рассмотрим некоторые подходы.
Оптимальное решение задачи даёт полный перебор. Если исходная система содержит  признаков, а нам нужно выбрать наилучшую подсистему, содержащую признаков, а нам нужно выбрать наилучшую подсистему, содержащую  признаков, то придётся рассмотреть признаков, то придётся рассмотреть 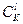 (число сочетаний из (число сочетаний из  элементов по элементов по  ) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15,5×103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор. ) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15,5×103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор.
Рис. 17. Переход к полярной системе координат
с последующим отбрасыванием признака 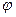
Рассмотрим некоторые из применяемых процедур.
1. Оценивается информативность каждого из исходных признаков, взятого в отдельности. Затем признаки ранжируются по убыванию информативности. После этого отбираются  первых признаков. Здесь число рассматриваемых вариантов первых признаков. Здесь число рассматриваемых вариантов  . При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным. . При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным.
2. Предполагается, что признаки статистически зависимы. Сначала отбирается самый индивидуально информативный признак (просматривается  вариантов). Затем к первому отобранному признаку присоединяется ещё один из оставшихся, составляющий с первым самую информативную пару (просматривается вариантов). Затем к первому отобранному признаку присоединяется ещё один из оставшихся, составляющий с первым самую информативную пару (просматривается  вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается  вариантов) и т.д. до получения совокупности из вариантов) и т.д. до получения совокупности из  признаков. Здесь число просматриваемых вариантов составляет величину признаков. Здесь число просматриваемых вариантов составляет величину  . Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе. . Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе.
3. Последовательное отбрасывание признаков. Этот подход похож на предыдущий. Из совокупности, содержащей  признаков, отбрасывается тот, который даёт минимальное уменьшение информативности. Затем из оставшейся совокупности, содержащей признаков, отбрасывается тот, который даёт минимальное уменьшение информативности. Затем из оставшейся совокупности, содержащей 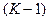 признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется  признаков. Из этих двух подходов (последовательное присоединение признаков и последовательное отбрасывание признаков) целесообразно использовать первый при признаков. Из этих двух подходов (последовательное присоединение признаков и последовательное отбрасывание признаков) целесообразно использовать первый при  и второй при и второй при  , если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным. , если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным.
4. Случайный поиск. Случайным образом отбираются номера  признаков и оценивается информативность этой подсистемы. Затем снова и независимо от предыдущего набора случайно формируется другая система из признаков и оценивается информативность этой подсистемы. Затем снова и независимо от предыдущего набора случайно формируется другая система из  признаков. Так повторяется признаков. Так повторяется 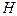 раз. Из раз. Из 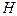 наборов признаков отбирается тот, который имеет наибольшую информативность. Чем наборов признаков отбирается тот, который имеет наибольшую информативность. Чем 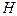 больше, тем выше вероятность выбора наилучшей подсистемы. При больше, тем выше вероятность выбора наилучшей подсистемы. При  можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности). можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности).
5. Случайный поиск с адаптацией. Это последовательная направленная процедура, основанная на случайном поиске с учётом результатов предыдущих отборов. В начале процедуры шансы всех исходных признаков на вхождение в подсистему, состоящую из  признаков, принимаются равными. Для случайного отбора используется датчик равномерно распределённых в интервале признаков, принимаются равными. Для случайного отбора используется датчик равномерно распределённых в интервале  случайных (псевдослучайных) чисел. Этот интервал разбивается на случайных (псевдослучайных) чисел. Этот интервал разбивается на  равных отрезков. Первый отрезок ставится в соответствие признаку равных отрезков. Первый отрезок ставится в соответствие признаку  , второй – , второй –  и т.д. Длина каждого отрезка равна вероятности и т.д. Длина каждого отрезка равна вероятности  включения включения  -го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается -го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается  различных отрезков. Для тех различных отрезков. Для тех  признаков из признаков из  , которые соответствуют этим отрезкам, определяется значение критерия информативности , которые соответствуют этим отрезкам, определяется значение критерия информативности  . После получения первой группы из . После получения первой группы из 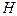 случайно выбранных подсистем определяется случайно выбранных подсистем определяется  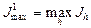 и и  . Адаптация состоит в изменении вектора вероятностей . Адаптация состоит в изменении вектора вероятностей  выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале  , соответствующая признаку, попавшему в самую плохую подсистему, уменьшается (признак "наказывается"), а попавшему в самую хорошую подсистему – увеличивается (признак "поощряется"). Длины отрезков изменяются на величину , соответствующая признаку, попавшему в самую плохую подсистему, уменьшается (признак "наказывается"), а попавшему в самую хорошую подсистему – увеличивается (признак "поощряется"). Длины отрезков изменяются на величину   . После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из . После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из  признаков. Чем больше признаков. Чем больше  , тем быстрее сходимость процедуры, но тем ниже вероятность "выхода" на наилучшую подсистему. И наоборот, чем меньше , тем быстрее сходимость процедуры, но тем ниже вероятность "выхода" на наилучшую подсистему. И наоборот, чем меньше  , тем медленнее сходимость, но выше вероятность выбора наилучшей подсистемы. Конкретный выбор значения , тем медленнее сходимость, но выше вероятность выбора наилучшей подсистемы. Конкретный выбор значения  должен быть таким, чтобы процедура сходилась при общем числе выборов должен быть таким, чтобы процедура сходилась при общем числе выборов  , а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице. , а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице.
СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
Говоря о статистических методах распознавания, мы предполагаем установление связи между отнесением объекта к тому или иному классу (образу) и вероятностью ошибки при решении этой задачи. В ряде случаев это сводится к определению апостериорной вероятности принадлежности объекта образу  при условии, что признаки этого объекта приняли значения при условии, что признаки этого объекта приняли значения  . .
Например, при условии, что плод красный и круглый, мы с большой долей уверенности можем предположить, что это яблоко, чем в случае, если эта информация отсутствует, т.е. апостериорная вероятность данного события будет P (яблоко|красный, круглый). Из сказанного становится понятным, почему она называется апостериорной (от лат. aposteriori - последующая, свершившаяся): ее можно определить только после того, как мы узнаем признаки объекта (красный, круглый).
Начнём с байесовского решающего правила. По формуле Байеса

Здесь  – априорная вероятность предъявления к распознаванию объекта – априорная вероятность предъявления к распознаванию объекта  -го образа: -го образа:
  . .
для каждого 
 , ,
при признаках с непрерывной шкалой измерений
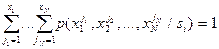 , ,
при признаках с дискретной шкалой измерений
 . .
При непрерывных значениях признаков  представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей. представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей.
Распределения, описывающие разные классы, как правило, "пересекаются", то есть имеются такие значения признаков  , при которых , при которых
 . .
В таких случаях ошибки распознавания неизбежны. Естественно, неинтересны случаи, когда эти классы (образы) в выбранной системе признаков  неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом). неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом).
В общем случае нужно стремиться выбрать решающие правила так, чтобы минимизировать риск потерь при распознавании.
Риск потерь определяется двумя компонентами: вероятностью ошибок распознавания и величиной "штрафа" за эти ошибки (потерями). Матрица ошибок распознавания:
 , ,
где  – вероятность правильного распознавания; – вероятность правильного распознавания;
 – вероятность ошибочного отнесения объекта – вероятность ошибочного отнесения объекта  -го образа к -го образа к  -му ( -му ( ). ).
Матрица потерь
  , ,
где  – "премия" за правильное распознавание; – "премия" за правильное распознавание;
 – "штраф" за ошибочное отнесение объекта – "штраф" за ошибочное отнесение объекта  -го образа к -го образа к  -му ( -му ( ). ).
Необходимо построить решающее правило так, чтобы обеспечить минимум математического ожидания потерь (минимум среднего риска). Такое правило называется байесовским.
Разобьём признаковое пространство 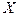 на на 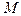 непересекающихся областей непересекающихся областей  , каждая из которых соответствует определённому образу. , каждая из которых соответствует определённому образу.
Средний риск при попадании реализаций  -го образа в области других образов равен -го образа в области других образов равен
 , ,  . .
Здесь предполагается, что все компоненты 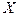 имеют непрерывную шкалу измерений (в данном случае это непринципиально). имеют непрерывную шкалу измерений (в данном случае это непринципиально).
Величину  можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта  -го образа). Общий (безусловный) средний риск определяется величиной -го образа). Общий (безусловный) средний риск определяется величиной 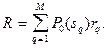
Решающие правила (способы разбиения 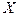 на на   ) образуют множество ) образуют множество 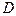 . Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск . Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск 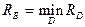 , где , где  – средний риск при применении одного из решающих правил, входящих в – средний риск при применении одного из решающих правил, входящих в 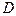 . .
Рассмотрим упрощённый случай. Пусть  , а , а  ( ( ). В таком случае байесовское решающее правило обеспечивает минимум вероятности (среднего количества) ошибок распознавания. Пусть ). В таком случае байесовское решающее правило обеспечивает минимум вероятности (среднего количества) ошибок распознавания. Пусть  . Вероятность ошибки первого рода (объект 1-го образа отнесён ко второму образу) . Вероятность ошибки первого рода (объект 1-го образа отнесён ко второму образу)
 , ,
где  – вероятность ошибки второго рода – вероятность ошибки второго рода
 . .
Средние ошибки
 . .
Так как  , то , то 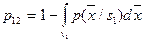 и и  . Ясно, что минимум . Ясно, что минимум  будет иметь минимум в том случае, если подынтегральное выражение в области будет иметь минимум в том случае, если подынтегральное выражение в области 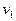 будет строго отрицательным, то есть в будет строго отрицательным, то есть в 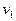  . В области . В области  должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе: должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе:  ; величина ; величина 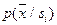 , рассматриваемая как функция от , рассматриваемая как функция от  , называется правдоподобием , называется правдоподобием  при данном при данном  , а , а  – отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение – отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение  в случае, если отношение правдоподобия превышает определённое пороговое значение, не зависящее от наблюдаемого в случае, если отношение правдоподобия превышает определённое пороговое значение, не зависящее от наблюдаемого  . .
Без специального рассмотрения укажем, что если число распознаваемых классов больше двух ( ), решение в пользу класса (образа) ), решение в пользу класса (образа)  принимается в области принимается в области  , в которой для всех , в которой для всех   . .
Иногда при невысокой точности оценки апостериорной вероятности (малых объёмах обучающей выборки) используют так называемые рандомизированные решающие правила. Они состоят в том, что неизвестный объект относят к тому или иному образу не по максимуму апостериорной вероятности, а случайным образом, в соответствии с апостериорными вероятностями этих образов  . Реализовать это можно, например, способом, изображённым на рис. 18. . Реализовать это можно, например, способом, изображённым на рис. 18.
   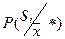  

0 1
Рис. 18. Иллюстрация рандомизированного решающего правила
После вычисления апостериорных вероятностей принадлежности неизвестного объекта с параметрами  каждому из образов каждому из образов  , ,  , отрезок прямой длиной единица разбивают на , отрезок прямой длиной единица разбивают на  интервалов с длинами, численно равными интервалов с длинами, численно равными 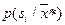 , и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределённых на , и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределённых на  , генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал. , генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал.
Понятно, что такое решающее правило не может быть лучше байесовского, но при больших значениях отношения правдоподобия ненамного ему уступает, а в реализации может оказаться достаточно простым (например, метод ближайшего соседа, о чём речь пойдёт позже).
Байесовское решающее правило реализуется в компьютерах в основном двумя способами.
1. Прямое вычисление апостериорных вероятностей
 , ,
где  – вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого – вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого 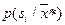 максимально. Иными словами, байесовское решающее правило реализуется решением задачи максимально. Иными словами, байесовское решающее правило реализуется решением задачи  . .
Если пойти на дальнейшее обобщение и допустить наличие матрицы потерь общего вида, то условный риск можно определить по формуле  , ,  . Здесь первый член определяет "поощрение" за правильное распознавание, а второй – "наказание" за ошибку. Байесовское решающее правило в данном случае состоит в решении задачи . Здесь первый член определяет "поощрение" за правильное распознавание, а второй – "наказание" за ошибку. Байесовское решающее правило в данном случае состоит в решении задачи

2. "Топографическое" определение области  , в которую попал вектор , в которую попал вектор  значений признаков, описывающих распознаваемый объект. значений признаков, описывающих распознаваемый объект.
Такой подход используют в тех случаях, когда описание областей  достаточно компактно, а процедура определения области, в которую попал достаточно компактно, а процедура определения области, в которую попал  , проста. Иными словами, данный подход естественно использовать, когда в вычислительном отношении он эффективнее (проще), чем прямое вычисление апостериорных вероятностей. , проста. Иными словами, данный подход естественно использовать, когда в вычислительном отношении он эффективнее (проще), чем прямое вычисление апостериорных вероятностей.
Рис. 19. Байесовское решающее правило
для нормально распределённых признаков
с равными ковариационными матрицами
Так, например (доказательство приводить не будем), если классов два, их априорные вероятности одинаковы,  и и  – нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков – нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков  этого объекта и по знаку (плюс или минус) получаемого решения относят объект к этого объекта и по знаку (плюс или минус) получаемого решения относят объект к  или или  (рис. 19). (рис. 19).
Если у классов  и и  ковариационные матрицы ковариационные матрицы  и и  не только одинаковы, но и диагональны, то байесовским решением является отнесение объекта к тому классу, евклидово расстояние до эталона которого минимально (рис. 20). не только одинаковы, но и диагональны, то байесовским решением является отнесение объекта к тому классу, евклидово расстояние до эталона которого минимально (рис. 20).

Рис. 20. Байесовское решающее правило
для нормально распределённых признаков
с равными диагональными ковариационными матрицами
(элементы диагоналей одинаковы)
Таким образом, мы убеждаемся в том, что некоторые решающие правила, ранее рассмотренные нами как эмпирические (детерминированные, эвристические), имеют вполне чёткую статистическую трактовку. Более того, в ряде конкретных случаев они являются статистически оптимальными. Список подобных примеров мы продолжим при дальнейшем рассмотрении статистических методов распознавания.
Теперь перейдём к методам оценки распределений значений признаков классов. Знание 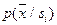 является наиболее универсальной информацией для решения задач распознавания статистическими методами. Эту информацию можно получить двояким образом: является наиболее универсальной информацией для решения задач распознавания статистическими методами. Эту информацию можно получить двояким образом:
заранее определить (оценить) 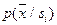 для всех для всех 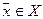 и и  ; ;
определять  при каждом акте распознавания конкретного объекта, признаки которого имеют значения при каждом акте распознавания конкретного объекта, признаки которого имеют значения  . .
Каждый из этих подходов имеет свои преимущества и недостатки, зависящие от числа признаков, объёма обучающей выборки, наличия априорной информации и т.п.
Начнём с локального варианта (определения  в окрестности распознаваемого объекта). в окрестности распознаваемого объекта).
1.10 Метод  ближайших соседей ближайших соседей
Здесь идея состоит в том, что вокруг распознаваемого объекта  строится ячейка объёма строится ячейка объёма  . При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа . При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа  , попавших в данную ячейку, характеризует оценку усреднённой по объёму , попавших в данную ячейку, характеризует оценку усреднённой по объёму  плотности вероятности плотности вероятности 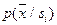 . .
Для оценки усреднённых 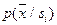 нужно решить вопрос о соотношении между объёмом нужно решить вопрос о соотношении между объёмом  ячейки и количеством попавших в эту ячейку объектов того или иного класса (образа). Вполне разумно считать, что чем меньше ячейки и количеством попавших в эту ячейку объектов того или иного класса (образа). Вполне разумно считать, что чем меньше  , тем более тонко будет охарактеризована , тем более тонко будет охарактеризована 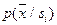 . Но при этом тем меньше объектов попадёт в интересующую нас ячейку, а следовательно, тем меньше достоверность оценки . Но при этом тем меньше объектов попадёт в интересующую нас ячейку, а следовательно, тем меньше достоверность оценки 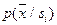 . При чрезмерном увеличении . При чрезмерном увеличении  возрастает достоверность оценки возрастает достоверность оценки 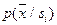 , но теряются тонкости её описания из-за усреднения по слишком большому объёму, что может привести к негативным последствиям (увеличению вероятности ошибок распознавания). При небольшом объёме обучающей выборки , но теряются тонкости её описания из-за усреднения по слишком большому объёму, что может привести к негативным последствиям (увеличению вероятности ошибок распознавания). При небольшом объёме обучающей выборки  целесообразно брать предельно большим, но обеспечить при этом, чтобы внутри ячейки плотности целесообразно брать предельно большим, но обеспечить при этом, чтобы внутри ячейки плотности 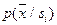 мало изменялись. Тогда их усреднение по большому объёму не очень опасно. Таким образом, вполне может случиться, что объём ячейки, уместный для одного значения мало изменялись. Тогда их усреднение по большому объёму не очень опасно. Таким образом, вполне может случиться, что объём ячейки, уместный для одного значения  , может совершенно не годиться для других случаев. , может совершенно не годиться для других случаев.
Предлагается следующий порядок действий (пока что принадлежность объекта тому или иному образу учитывать не будем).
Для того чтобы оценить  на основании обучающей выборки, содержащей на основании обучающей выборки, содержащей 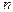 объектов, центрируем ячейку вокруг объектов, центрируем ячейку вокруг  и увеличиваем её объём до тех пор, пока она не вместит и увеличиваем её объём до тех пор, пока она не вместит  объектов, где объектов, где  есть некоторая функция от есть некоторая функция от 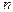 . Эти . Эти  объектов будут ближайшими соседями объектов будут ближайшими соседями  . Вероятность . Вероятность  попадания вектора попадания вектора  в область в область  определяется выражением определяется выражением 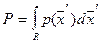 . .
Это сглаженный (усреднённый) вариант плотности распределения  . Если взять выборку из . Если взять выборку из 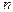 объектов (простым случайным выбором из генеральной совокупности), то объектов (простым случайным выбором из генеральной совокупности), то 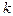 из них окажется внутри области из них окажется внутри области  . Вероятность попадания . Вероятность попадания 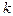 из из 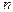 объектов в объектов в  описывается биномиальным законом, имеющим резко выраженный максимум около среднего значения описывается биномиальным законом, имеющим резко выраженный максимум около среднего значения  . При этом . При этом  является неплохой оценкой для является неплохой оценкой для  . .
Если теперь допустить, что  настолько мала, что настолько мала, что  внутри неё меняется незначительно, то внутри неё меняется незначительно, то
 , ,
где  – объём области – объём области  , ,  – точка внутри – точка внутри  . .
Тогда  . Но . Но 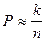 , следовательно, , следовательно,  . .
Итак, оценкой  плотности плотности  является величина является величина
 . (*) . (*)
Без доказательства приведём утверждение, что условия
 и и  (**) (**)
являются необходимыми и достаточными для сходимости  к к  по вероятности во всех точках, где плотность по вероятности во всех точках, где плотность  непрерывна. непрерывна.
Этому условию удовлетворяет, например, 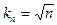 . .
Теперь будем учитывать принадлежность объектов к тому или иному образу и попытаемся оценить апостериорные вероятности образов 
Предположим, что мы размещаем ячейку объёма  вокруг вокруг  и захватываем выборку с количеством объектов и захватываем выборку с количеством объектов  , ,  из которых принадлежат образу из которых принадлежат образу  . Тогда в соответствии с формулой . Тогда в соответствии с формулой  оценкой совместной вероятности оценкой совместной вероятности  будет величина будет величина
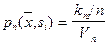 , ,
а
 . .
Таким образом, апостериорная вероятность 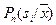 оценивается как доля выборки в ячейке, относящаяся к оценивается как доля выборки в ячейке, относящаяся к  . Чтобы свести уровень ошибки к минимуму, нужно объект с координатами . Чтобы свести уровень ошибки к минимуму, нужно объект с координатами  отнести к классу (образу), количество объектов обучающей выборки которого в ячейке максимально. При отнести к классу (образу), количество объектов обучающей выборки которого в ячейке максимально. При  такое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок распознавания (разумеется, при этом должны выполняться условия такое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок распознавания (разумеется, при этом должны выполняться условия  ). ).
Правило ближайшего соседа
Пусть  – множество объектов обучающей последовательности, то есть принадлежность каждого из них тому или иному образу достоверно известна. Пусть также – множество объектов обучающей последовательности, то есть принадлежность каждого из них тому или иному образу достоверно известна. Пусть также  является объектом, ближайшим к распознаваемому является объектом, ближайшим к распознаваемому  . Напомним, что при этом правило ближайшего соседа для классификации . Напомним, что при этом правило ближайшего соседа для классификации  | 


 – исходное признаковое пространство,
– исходное признаковое пространство,  – преобразованное признаковое пространство,
– преобразованное признаковое пространство,  – некоторая функция.
– некоторая функция.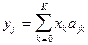 .
. не несёт различительной информации и его использование для распознавания не имеет смысла.
не несёт различительной информации и его использование для распознавания не имеет смысла. .
.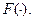 Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование.
Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование.






 ,
, – диагональная матрица, причём её элементы равны либо 0, либо 1.
– диагональная матрица, причём её элементы равны либо 0, либо 1. признаков, а нам нужно выбрать наилучшую подсистему, содержащую
признаков, а нам нужно выбрать наилучшую подсистему, содержащую  признаков, то придётся рассмотреть
признаков, то придётся рассмотреть 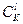 (число сочетаний из
(число сочетаний из  ) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15,5×103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор.
) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15,5×103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор.
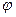
 . При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным.
. При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным. вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается
вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается  вариантов) и т.д. до получения совокупности из
вариантов) и т.д. до получения совокупности из  . Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе.
. Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе.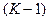 признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется
признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется  и второй при
и второй при  , если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным.
, если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным.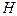 раз. Из
раз. Из  можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности).
можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности). случайных (псевдослучайных) чисел. Этот интервал разбивается на
случайных (псевдослучайных) чисел. Этот интервал разбивается на  , второй –
, второй –  и т.д. Длина каждого отрезка равна вероятности
и т.д. Длина каждого отрезка равна вероятности  включения
включения  -го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается
-го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается  различных отрезков. Для тех
различных отрезков. Для тех  . После получения первой группы из
. После получения первой группы из 
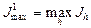 и
и  . Адаптация состоит в изменении вектора вероятностей
. Адаптация состоит в изменении вектора вероятностей  выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале
выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале 
 . После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из
. После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из  , а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице.
, а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице. .
.
 – априорная вероятность предъявления к распознаванию объекта
– априорная вероятность предъявления к распознаванию объекта  -го образа:
-го образа:
 .
.
 ,
,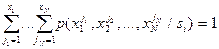 ,
, .
. представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей.
представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей. , при которых
, при которых .
. неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом).
неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом). ,
, – вероятность правильного распознавания;
– вероятность правильного распознавания; – вероятность ошибочного отнесения объекта
– вероятность ошибочного отнесения объекта  ).
). ,
, – "премия" за правильное распознавание;
– "премия" за правильное распознавание; – "штраф" за ошибочное отнесение объекта
– "штраф" за ошибочное отнесение объекта 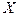 на
на 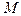 непересекающихся областей
непересекающихся областей  , каждая из которых соответствует определённому образу.
, каждая из которых соответствует определённому образу. -го образа в области других образов равен
-го образа в области других образов равен ,
,  .
. можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта
можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта 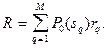

 ) образуют множество
) образуют множество 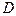 . Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск
. Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск 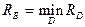 , где
, где  – средний риск при применении одного из решающих правил, входящих в
– средний риск при применении одного из решающих правил, входящих в  , а
, а  (
( . Вероятность ошибки первого рода (объект 1-го образа отнесён ко второму образу)
. Вероятность ошибки первого рода (объект 1-го образа отнесён ко второму образу) ,
, – вероятность ошибки второго рода
– вероятность ошибки второго рода .
. .
. , то
, то 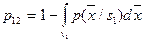 и
и  . Ясно, что минимум
. Ясно, что минимум  будет иметь минимум в том случае, если подынтегральное выражение в области
будет иметь минимум в том случае, если подынтегральное выражение в области 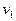 будет строго отрицательным, то есть в
будет строго отрицательным, то есть в  . В области
. В области  должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе:
должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе:  ; величина
; величина 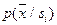 , рассматриваемая как функция от
, рассматриваемая как функция от  , называется правдоподобием
, называется правдоподобием  , а
, а  – отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение
– отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение  в случае, если отношение правдоподобия превышает определённое пороговое значение, не зависящее от наблюдаемого
в случае, если отношение правдоподобия превышает определённое пороговое значение, не зависящее от наблюдаемого  ), решение в пользу класса (образа)
), решение в пользу класса (образа)  принимается в области
принимается в области  , в которой для всех
, в которой для всех 
 .
. . Реализовать это можно, например, способом, изображённым на рис. 18.
. Реализовать это можно, например, способом, изображённым на рис. 18.


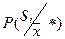


 каждому из образов
каждому из образов  , отрезок прямой длиной единица разбивают на
, отрезок прямой длиной единица разбивают на  интервалов с длинами, численно равными
интервалов с длинами, численно равными 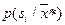 , и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределённых на
, и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределённых на  , генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал.
, генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал. ,
, – вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого
– вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого  .
. ,
, 
 , в которую попал вектор
, в которую попал вектор 
 и
и  – нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков
– нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков 
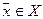 и
и  ;
; при каждом акте распознавания конкретного объекта, признаки которого имеют значения
при каждом акте распознавания конкретного объекта, признаки которого имеют значения  ближайших соседей
ближайших соседей . При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа
. При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа  , попавших в данную ячейку, характеризует оценку усреднённой по объёму
, попавших в данную ячейку, характеризует оценку усреднённой по объёму  на основании обучающей выборки, содержащей
на основании обучающей выборки, содержащей 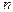 объектов, центрируем ячейку вокруг
объектов, центрируем ячейку вокруг  объектов, где
объектов, где  попадания вектора
попадания вектора  определяется выражением
определяется выражением 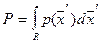 .
.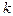 из них окажется внутри области
из них окажется внутри области  . При этом
. При этом  является неплохой оценкой для
является неплохой оценкой для  ,
, . Но
. Но 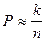 , следовательно,
, следовательно,  .
. плотности
плотности  . (*)
. (*) и
и  (**)
(**)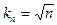 .
.
 из которых принадлежат образу
из которых принадлежат образу  . Тогда в соответствии с формулой
. Тогда в соответствии с формулой  оценкой совместной вероятности
оценкой совместной вероятности  будет величина
будет величина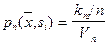 ,
, .
.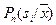 оценивается как доля выборки в ячейке, относящаяся к
оценивается как доля выборки в ячейке, относящаяся к  такое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок распознавания (разумеется, при этом должны выполняться условия
такое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок распознавания (разумеется, при этом должны выполняться условия  ).
). – множество объектов обучающей последовательности, то есть принадлежность каждого из них тому или иному образу достоверно известна. Пусть также
– множество объектов обучающей последовательности, то есть принадлежность каждого из них тому или иному образу достоверно известна. Пусть также  является объектом, ближайшим к распознаваемому
является объектом, ближайшим к распознаваемому  . Напомним, что при этом правило ближайшего соседа для классификации
. Напомним, что при этом правило ближайшего соседа для классификации 


