
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1 Задача распознавания образовСодержание книги
Поиск на нашем сайте Е.А. Корчевская Распознавание образов Лекционные материалы по дисциплине «Распознавание образов» для студентов 4 курса специальности Прикладная математика (1-31 03 03) Витебск, 2011 Лекция 1 Задача распознавания образов Предмет распознавания образов Распознавание образов – это научная дисциплина, целью которой является классификация объектов по нескольким категориям или классам. Объекты называются образами. Образ – классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку. Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. В классической постановке задачи распознавания универсальное множество разбивается на части–образы. Каждое отображение какого–либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображением объекта, а множества таких изображений, объединенные какими–либо общими свойствами, представляют собой образы. Класс – множество объектов, сходных по природе и признакам. Классификация – процедура отнесения к тому или иному классу. Идентификация – предельный случай классификации, когда класс состоит из одного объекта. Аналитический признак – измеряемая величина, зависящая от природы объекта и по возможности не зависящая от количества объекта. Прецедент – это образ, правильная классификация которого известна. Прецедент – ранее классифицированный объект, принимаемый как образец при решении задач классификации. Идея принятия решений на основе прецедентности – основополагающая в естественно-научном мировоззрении. Будем считать, что все объекты или явления разбиты на конечное число классов. Для каждого класса известно и изучено конечное число объектов – прецедентов. Задача распознавания образов состоит в том, чтобы отнести новый распознаваемый объект к какому-либо классу. Задача распознавания образов является основной в большинстве интеллектуальных систем. Рассмотрим примеры интеллектуальных компьютерных систем. 1) Машинное зрение. Это системы, назначение которых состоит в получении изображения через камеру и составление его описания в символьном виде (какие объекты присутствуют, в каком взаимном отношении находятся и т.д.). 2) Символьное распознавание – это распознавание букв или цифр. b. Ввод и хранение документов; d. Обработка чеков в банках; e. Обработка почты. 3) Диагностика в медицине. a. Маммография, рентгенография; b. Постановка диагноза по истории болезни; c. Электрокардиограмма. 4) Геология. 5) Распознавание речи. 6) Распознавание в дактилоскопии (отпечатки пальцев), распознавание лица, подписи, жестов. В целом проблема распознавания образов состоит из двух частей: обучения и распознавания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлежности тому или другому образу. В результате обучения распознающая система должна приобрести способность реагировать одинаковыми реакциями на все объекты одного образа и различными - на все объекты различных образов. Очень важно, что процесс обучения должен завершиться только путем показов конечного числа объектов без каких-либо других подсказок. В качестве объектов обучения могут быть либо картинки, либо другие визуальные изображения (буквы), либо различные явления внешнего мира, например звуки, состояния организма при медицинском диагнозе, состояние технического объекта в системах управления и др. Важно, что в процессе обучения указываются только сами объекты и их принадлежность образу. За обучением следует процесс распознавания новых объектов, который характеризует действия уже обученной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В том случае, когда человек сам разгадывает или придумывает, а затем навязывает машине правило классификации, проблема распознавания решается частично, так как основную и главную часть проблемы (обучение) человек берет на себя. Обучающая выборка – множество образов объектов, охватывающее все классы. Методика отнесения элемента к какому–либо образу называется решающим правилом. Обучение – это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация – это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий. Адаптация – это процесс изменения параметров и структуры системы, а возможно – и управляющих воздействий, на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы. Классификация основывается на прецедентах. Признаки и классификаторы Измерения, используемые для классификации образов, называются признаками. Признак– это некоторое количественное измерение объекта произвольной природы. Совокупность признаков, относящихся к одному образу, называется вектором признаков. Вектора признаков принимают значения в пространстве признаков. В рамках задачи распознавания считается, что каждому образу ставится в соответствие единственное значение вектора признаков и наоборот: каждому значению вектора признаков соответствует единственный образ. Классификатором или решающим правилом называется правило отнесения образа к одному из классов на основании его вектора признаков. Пример 1. Иллюстрация понятий признаков и классификатора и идеи распознавания (классификации). Рассмотрим задачу диагностики печени по результатам инструментального исследования (рис.1.1). Доброкачественные (левый рисунок – класс A) и злокачественные (правый рисунок – класс B) изменения дают разную картину. Предположим, что имеется несколько препаратов в базе данных, про которые известна их принадлежность к классам A и B (правильная классификация). Очевидно, что образцы отличаются интенсивностью точек изображения. В качестве вектора признаков выберем пару: среднее значение (
Рис. 1. Образы-прецеденты, соответствующие классу A (слева) и B (справа)
Рис. 2. Распределение векторов признаков прецедентах класса A (кружки) и класса B (крестики). Признаки - средние значения и средние отклонения яркости в образах. Прямая линия разделяет вектора из разных классов На рис.2 представлены изображения этих образов в пространстве признаков. Точки, соответствующие прецедентам разных классов, разделяются прямой линией. Классификация неизвестного образа (соответствующая точка изображена звездочкой) состоит в проверке положения точки относительно этой разделяющей прямой. Практическая разработка системы классификации осуществляется по следующей схеме. В процессе разработки необходимо решить следующие вопросы.
Рис.3. Основные элементы построения системы распознавания образов (классификации) 1. Как выбрать вектора признаков? Задача генерации признаков – это выбор тех признаков, которые с достаточной полнотой (в разумных пределах) описывают образ. 2. Какие признаки наиболее существенны для разделения объектов разных классов? Задача селекции признаков – отбор наиболее информативных признаков для классификации. 3. Как построить классификатор? Задача построения классификатора – выбор решающего правила, по которому на основании вектора признаков осуществляется отнесение объекта к тому или иному классу. 4. Как оценить качество построенной системы классификации? Задача количественной оценки системы (выбранные признаки + классификатор) с точки зрения правильности или ошибочности классификации. Методы распознавания Выделяют 4 группы методов распознавания: ¾ Сравнение с образцом. Применяем геометрическую нормализацию и считаем расстояние до прототипа. ¾ Статистические методы. Строим распределение для каждого класса и классифицируем по правилу Байеса. Распределение можно построить, используя тренировочную коллекцию. ¾ Нейронные сети. Выбираем вид сети и настраиваем коэффициенты. На вход нейронной сети подается распознаваемый объект. С одной стороны сети расположены рецепторы, каждый из которых отвечает за прием своего характеристического свойства распознаваемых объектов. С другой стороны сети расположены эффекторы, каждый из которых соответствует одному из образов. Выбираем тот из коэффициентов, значение в котором максимально. Настройка коэффициентов является фазой обучения алгоритма. Ha этом этапе мы настраиваем коэффициенты таким образом, чтобы алгоритм правильно работал на образцах. Чем больше образцов, тем больше вероятность того, что алгоритм примет верное решение на остальных данных. ¾ Структурные и синтаксические методы. Разбираем объект на элементы. Строим правило, в зависимости от вхождения/не вхождения отдельных элементов и их последовательностей.
Построение решающих правил Для построения решающих правил нужна обучающая выборка. Обучающая выборка – это множество объектов, заданных значениями признаков и принадлежность которых к тому или иному классу достоверно известна "учителю" и сообщается учителем "обучаемой" системе. По обучающей выборке система строит решающие правила. Качество решающих правил оценивается по контрольной (экзаменационной) выборке, в которую входят объекты, заданные значениями признаков, и принадлежность которых тому или иному образу известна только учителю. Предъявляя обучаемой системе для контрольного распознавания объекты экзаменационной выборки, учитель в состоянии дать оценку вероятностей ошибок распознавания, то есть оценить качество обучения. К обучающей и контрольной выборкам предъявляются определённые требования. Например, важно, чтобы объекты экзаменационной выборки не входили в обучающую выборку (иногда, правда, это требование нарушается, если общий объём выборок мал и увеличить его либо невозможно, либо чрезвычайно сложно). Обучающая и экзаменационная выборки должны достаточно полно представлять генеральную совокупность (гипотетическое множество всех возможных объектов каждого образа). Например, при обучении системы медицинской диагностики в обучающей и контрольной выборках должны быть представлены пациенты различных половозрастных групп, с различными анатомическими и физиологическими особенностями, сопутствующими заболеваниями и т.д. При социологических исследованиях это называют репрезентативностью выборки. Итак, для построения решающих правил системе предъявляются объекты, входящие в обучающую выборку. Метод построения эталонов Для каждого класса по обучающей выборке строится эталон, имеющий значения признаков
где
По существу, эталон – это усреднённый по обучающей выборке абстрактный объект (рис. 2). Абстрактным мы его называем потому, что он может не совпадать не только ни с одним объектом обучающей выборки, но и ни с одним объектом генеральной совокупности. Распознавание осуществляется следующим образом. На вход системы поступает объект
Рис. 2. Решающее правило "Минимум расстояния
– эталон второго класса Метод дробящихся эталонов Процесс обучения состоит в следующем. На первом этапе в обучающей выборке " охватывают " все объекты каждого класса гиперсферой возможно меньшего радиуса. Сделать это можно, например, так. Строится эталон каждого класса. Вычисляется расстояние от эталона до всех объектов данного класса, входящих в обучающую выборку. Выбирается максимальное из этих расстояний
Рис. 3. Решающее правило типа “Метод дробящихся эталонов” Если гиперсферы различных образов пересекаются и в области перекрытия оказываются объекты более чем одного образа, то для них строятся гиперсферы второго уровня, затем третьего и т.д. до тех пор, пока области не окажутся непересекающимися, либо в области пересечения будут присутствовать объекты только одного образа. Распознавание осуществляется следующим образом. Определяется местонахождение объекта относительно гиперсфер первого уровня. При попадании объекта в гиперсферу, соответствующую одному и только одному образу, процедура распознавания прекращается. Если же объект оказался в области перекрытия гиперсфер, которая при обучении содержала объекты более чем одного образа, то переходим к гиперсферам второго уровня и проводим действия такие же, как для гиперсфер первого уровня. Этот процесс продолжается до тех пор, пока принадлежность неизвестного объекта тому или иному образу не определится однозначно. Правда, это событие может и не наступить. В частности, неизвестный объект может не попасть ни в одну из гиперсфер какого-либо уровня. В этих случаях "учитель" должен включить в решающие правила соответствующие действия. Например, система может либо отказаться от решения об однозначном отнесении объекта к какому-либо образу, либо использовать критерий минимума расстояния до эталонов данного или предшествующего уровня и т.п. Какой из этих приёмов эффективнее, сказать трудно, т.к. метод дробящихся эталонов носит в основном эмпирический характер. Линейные решающие правила Само название говорит о том, что граница, разделяющая в признаковом пространстве области различных образов, описывается линейной функцией (рис. 4)
Рис. 4. Линейное решающее правило для распознавания Одна граница при этом разделяет области двух образов. Если
если
если то образы Существуют различные методы построения линейных решающих правил. Рассмотрим один из них, реализованный в 50-х годах Розенблатом, в устройствах распознавания изображений, названных персептронами (рис. 5). Пусть
где
Рис. 5. Упрощённая схема однослойного персептрона Выбор 1. 2. 3. Это правило вполне логично. Если очередной объект системой классифицирован правильно, то нет оснований изменять
Соответственно в случае (3) Важное значение имеет выбор
Если же выборки линейно неразделимы (рис. 6), то сходимость отсутствует и оценку Метод ближайших соседей Обучение в данном случае состоит в запоминании всех объектов обучающей выборки. Если системе предъявлен нераспознанный объект
Это правило ближайшего соседа. Правило Для сокращения числа запоминаемых объектов можно применять комбинированные решающие правила, например сочетание метода дробящихся эталонов и ближайших соседей. В этом случае запоминанию подлежат те объекты, которые попали в зону пересечения гиперсфер какого-либо уровня. Метод ближайших соседей применяется лишь для тех распознаваемых объектов, которые попали в данную зону пересечения. Иными словами, запоминанию подлежат не все объекты обучающей выборки, а только те, которые находятся вблизи разделяющей образы границы.
Языки описания образов Лекция 5 Кластерный анализ Кластерный анализ (самообучение, обучение без учителя, таксономия) применяется при автоматическом формировании перечня образов по обучающей выборке. Все объекты этой выборки предъявляются системе без указания, какому образу они принадлежат. Подобного рода задачи решает, например, человек в процессе естественно-научного познания окружающего мира (классификации растений, животных). Этот опыт целесообразно использовать при создании соответствующих алгоритмов. В основе кластерного анализа лежит гипотеза компактности. Предполагается, что обучающая выборка в признаковом пространстве состоит из набора сгустков. Задача системы – выявить и формализовано описать эти сгустки. Геометрическая интерпретация гипотезы компактности состоит в следующем. Объекты, относящиеся к одному таксону, расположены близко друг к другу по сравнению с объектами, относящимися к разным таксонам. "Близость" можно понимать шире, чем при геометрической интерпретации. Например, закономерность, описывающая взаимосвязь объектов одного таксона, отличается от таковой в других таксонах, как это имеет место в лингвистических методах. Мы ограничимся рассмотрением геометрической интерпретации. Остановимся на алгоритме FOREL (рис. 1).
Рис. 1. Иллюстрация алгоритма FOREL:
Строится гиперсфера радиуса В следующем цикле используются гиперсферы радиуса
Примером использования человеческих критериев при решении задач таксономии служит алгоритм KRAB. Эти критерии отработаны на двухмерном признаковом пространстве в ходе таксономии, осуществляемой человеком, и применены в алгоритме, функционирующем с объектами произвольной размерности. Факторы, выявленные при "человеческой" таксономии, можно сформулировать следующим образом: – внутри таксонов объекты должны быть как можно ближе друг к другу (обобщённый показатель – таксоны должны как можно дальше отстоять друг от друга (обобщённый показатель – в таксонах количество объектов должно быть по возможности одинаковым, то есть их различие в разных таксонах нужно минимизировать (обобщённый показатель – внутри таксонов не должно быть больших скачков плотности точек, то есть количества точек на единицу объёма (обобщённый показатель Если удастся удачно подобрать способы измерения Все точки обучающей выборки объединяются в граф, в котором они являются вершинами. Этот граф должен иметь минимальную суммарную длину рёбер, соединяющих все вершины, и не содержать петель (рис. 15). Такой граф называют КНП-графом (КНП – кратчайший незамкнутый путь).
Мера близости объектов в одном таксоне – это средняя длина ребра
где
Усреднённая по всем таксонам мера близости точек Средняя длина рёбер, соединяющих таксоны, Мера локальной неоднородности определяется следующим образом. Если длина
где Определим величину
Можно показать, что при фиксированном Теперь можно сформировать интегрированный критерий качества таксономии
Чем больше Метод потенциальных функций Название метода в определённой степени связано со следующей аналогией (для простоты будем считать, что распознаётся два образа). Представим себе, что объекты являются точками
Рис. 8. Иллюстрация синтеза потенциальной функции
Функцию, описывающую распределение электростатического потенциала в таком поле, можно использовать в качестве решающего правила (или для его построения). Если потенциал точки
Распознавание может осуществляться следующим способом. В точке При большом объёме обучающей выборки эти вычисления достаточно громоздки, и зачастую выгоднее вычислять не Выбор вида потенциальных функций – дело непростое. Например, если они очень быстро убывают с ростом расстояния, то можно добиться безошибочного разделения обучающих выборок. Однако при этом возникают определённые неприятности при распознавании неопознанных объектов (снижается достоверность принимаемого решения, возрастает зона неопределённости). При слишком "пологих" потенциальных функциях может необоснованно увеличиться количество ошибок распознавания, в том числе и на обучающих объектах. Определённые рекоменд
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |

 ) и среднеквадратичное отклонение (
) и среднеквадратичное отклонение ( ) интенсивности в изображении.
) интенсивности в изображении.


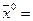
 ,
, =
=  ,
, – количество объектов данного образа в обучающей выборке,
– количество объектов данного образа в обучающей выборке, – номер признака.
– номер признака. 
 , принадлежность которого к тому или иному образу системе неизвестна. От этого объекта измеряются расстояния до эталонов всех образов, и
, принадлежность которого к тому или иному образу системе неизвестна. От этого объекта измеряются расстояния до эталонов всех образов, и 
 – эталон первого класса,
– эталон первого класса,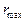 . Строится гиперсфера с центром в эталоне и радиусом
. Строится гиперсфера с центром в эталоне и радиусом  =
= 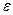 . Она охватывает все объекты данного класса. Такая процедура проводится для всех классов (образов). На рис. 3 приведён пример двух образов в двухмерном признаковом пространстве.
. Она охватывает все объекты данного класса. Такая процедура проводится для всех классов (образов). На рис. 3 приведён пример двух образов в двухмерном признаковом пространстве.
 =
= 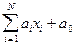 .
.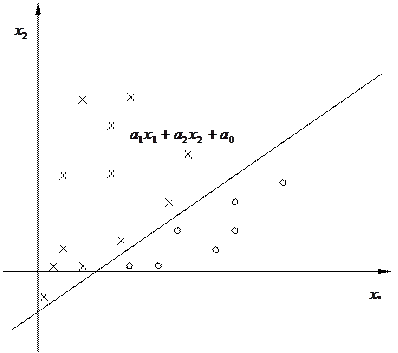
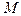 >2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать
>2, то требуется несколько линейных функций и граница является, вообще говоря, кусочно линейной. Для наглядности будем считать 

 ,
, – реализация первого образа
– реализация первого образа  ,
,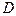
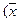

 ,
,

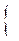
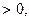 если
если 

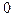 , если
, если  – некоторый объект одного из образов,
– некоторый объект одного из образов, 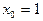 .
.
 осуществляется пошаговым образом.
осуществляется пошаговым образом. 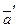 после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу:
после предъявления персептрону очередного объекта обучающей выборки. Эта корректировка производится по следующему правилу: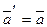 , если
, если  и
и  или если
или если  и
и  .
. , если
, если  ,
,  .
. , если
, если  .
. . Предложенное правило удовлетворяет этому требованию. Действительно,
. Предложенное правило удовлетворяет этому требованию. Действительно,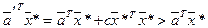 .
.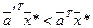 .
. . Можно, в частности, выбрать
. Можно, в частности, выбрать  . При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения
. При этом показано, что если обучающие выборки двух образов линейно разделимы, то описанная пошаговая процедура сходится, то есть будут найдены значения 
 , если
, если 

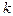 ближайших соседей состоит в том, что строится гиперсфера объёма
ближайших соседей состоит в том, что строится гиперсфера объёма  с центром в
с центром в 

 , где
, где  соответствует гиперсфере, охватывающей все объекты (точки) обучающей выборки. При этом число таксонов
соответствует гиперсфере, охватывающей все объекты (точки) обучающей выборки. При этом число таксонов  будет равно единице. Затем строится гиперсфера радиуса
будет равно единице. Затем строится гиперсфера радиуса  с центром в произвольной точке выборки. По множеству точек, попавших внутрь гиперсферы (формального элемента), определяется среднее значение координат (эталон) и в него перемещается центр гиперсферы. Если это перемещение существенное, то заметно изменится множество точек, попавших внутрь гиперсферы, а следовательно, и их среднее значение координат. Вновь перемещаем центр гиперсферы в это новое среднее значение и т.д. до тех пор, пока гиперсфера не остановится либо зациклится. Тогда все точки, попавшие внутрь этой гиперсферы, исключаются из рассмотрения и процесс повторяется на оставшихся точках. Это продолжается до тех пор, пока не будут исчерпаны все точки. Результат таксономии: набор гиперсфер (формальных элементов) радиуса
с центром в произвольной точке выборки. По множеству точек, попавших внутрь гиперсферы (формального элемента), определяется среднее значение координат (эталон) и в него перемещается центр гиперсферы. Если это перемещение существенное, то заметно изменится множество точек, попавших внутрь гиперсферы, а следовательно, и их среднее значение координат. Вновь перемещаем центр гиперсферы в это новое среднее значение и т.д. до тех пор, пока гиперсфера не остановится либо зациклится. Тогда все точки, попавшие внутрь этой гиперсферы, исключаются из рассмотрения и процесс повторяется на оставшихся точках. Это продолжается до тех пор, пока не будут исчерпаны все точки. Результат таксономии: набор гиперсфер (формальных элементов) радиуса  с центрами, определёнными в результате вышеописанной процедуры. Назовём это циклом с формальными элементами радиуса
с центрами, определёнными в результате вышеописанной процедуры. Назовём это циклом с формальными элементами радиуса  . Здесь появляется параметр
. Здесь появляется параметр  , определяемый исследователем чаще всего подбором в поисках компромисса: увеличение
, определяемый исследователем чаще всего подбором в поисках компромисса: увеличение  несколько циклов с радиусами формальных элементов
несколько циклов с радиусами формальных элементов  будут завершаться при одинаковом числе
будут завершаться при одинаковом числе 
 );
); );
); );
); ).
). и
и  то можно добиться хорошего совпадения "человеческой" и автоматической таксономии. В алгоритме KRAB используется следующий подход.
то можно добиться хорошего совпадения "человеческой" и автоматической таксономии. В алгоритме KRAB используется следующий подход.
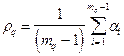 ,
, – число объектов в таксоне
– число объектов в таксоне  ,
, – длина
– длина  -го ребра.
-го ребра. .
. .
. , то чем меньше
, то чем меньше  , тем больше отличие в длинах рёбер, тем больше оснований считать, что по ребру с длиной
, тем больше отличие в длинах рёбер, тем больше оснований считать, что по ребру с длиной 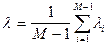 ,
, – общее число точек в обучающей выборке.
– общее число точек в обучающей выборке. .
.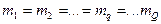 .
. .
. , тем это качество выше. Таким образом, осуществляя таксономию, нужно стремиться к максимизации
, тем это качество выше. Таким образом, осуществляя таксономию, нужно стремиться к максимизации  рёбер, таких, чтобы критерий
рёбер, таких, чтобы критерий  некоторого пространства
некоторого пространства 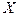 . В эти точки будем помещать заряды
. В эти точки будем помещать заряды  , если объект принадлежит образу
, если объект принадлежит образу  , если объект принадлежит образу
, если объект принадлежит образу 
 – потенциальная функция, порождаемая одиночным объектом;
– потенциальная функция, порождаемая одиночным объектом; – суммарная потенциальная функция, порождённая обучающей последовательностью
– суммарная потенциальная функция, порождённая обучающей последовательностью , то общий потенциал в
, то общий потенциал в 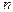 зарядами, равен
зарядами, равен
 и монотонно убывающая до нуля при
и монотонно убывающая до нуля при  .
. . Если он оказывается положительным, то объект относят к образу
. Если он оказывается положительным, то объект относят к образу 


