Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация с обучением и без обученияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В зависимости от наличия или отсутствия прецедентной информации различают задачи распознавания с обучением и без обучения. Задача распознавания на основе имеющегося множества прецедентов называется классификацией с обучением (или с учителем). В том случае, если имеется множество векторов признаков, полученных для некоторого набора образов, но правильная классификация этих образов неизвестна, возникает задача разделения этих образов на классы по сходству соответствующих векторов признаков. Эта задача называется кластеризацией или распознаванием без обучения. Пример 2. Рассмотрим съемку со спутника и классификацию поверхности по отраженной энергии (рис.3). На рисунке изображены снимок из космоса (слева) и результат кластеризации векторов признаков, рассчитанных для различных элементов изображения (справа). Распределение образов, изображенных точками (x1,x2) по классам осуществляется на основе анализа «скоплений» этих точек в пространстве признаков. Пример 3. Рассмотрим другой пример распознавания образов – в общественных (социальных) науках. Целью задачи является построение системы классификации государств для определения необходимости гуманитарной поддержки со стороны международных организаций. Необходимо выявить закономерности связей между различными, объективно измеряемыми параметрами, например, связь между ВНП, уровнем грамотности и уровнем детской смертности. В данном случае страны можно представить трехмерными векторами, а задача заключается в построении меры сходства этих векторов и дальнейшем построении схемы кластеризации (выбора групп) по этой мере. Еще одно важное понятие – метрика, способ определения расстояния между элементами универсального множества. Чем меньше это расстояние, тем более похожими являются объекты (символы, звуки и др.) – то, что мы распознаем. Обычно элементы задаются в виде набора чисел, а метрика – в виде функции. От выбора представления образов и реализации метрики зависит эффективность программы, один алгоритм распознавания с разными метриками будет ошибаться с разной частотой.
Формальная постановка задачи классификации Будем использовать следующую модель задачи классификации. Ω– множество объектов распознавания (пространство образов). ω: ω Задача заключается в построении такого решающего правила
Лекция 2 Методологические и алгоритмические основы процесса распознавания изображения Методы распознавания Выделяют 4 группы методов распознавания: ¾ Сравнение с образцом. Применяем геометрическую нормализацию и считаем расстояние до прототипа. ¾ Статистические методы. Строим распределение для каждого класса и классифицируем по правилу Байеса. Распределение можно построить, используя тренировочную коллекцию. ¾ Нейронные сети. Выбираем вид сети и настраиваем коэффициенты. На вход нейронной сети подается распознаваемый объект. С одной стороны сети расположены рецепторы, каждый из которых отвечает за прием своего характеристического свойства распознаваемых объектов. С другой стороны сети расположены эффекторы, каждый из которых соответствует одному из образов. Выбираем тот из коэффициентов, значение в котором максимально. Настройка коэффициентов является фазой обучения алгоритма. Ha этом этапе мы настраиваем коэффициенты таким образом, чтобы алгоритм правильно работал на образцах. Чем больше образцов, тем больше вероятность того, что алгоритм примет верное решение на остальных данных. ¾ Структурные и синтаксические методы. Разбираем объект на элементы. Строим правило, в зависимости от вхождения/не вхождения отдельных элементов и их последовательностей.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 962; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.008 с.) |


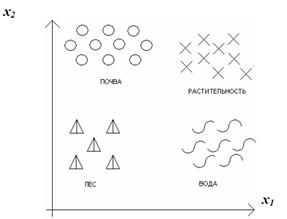
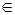 Ω – объект распознавания (образ). g (ω):Ω →M, M = {1,2,..., m } – индикаторная функция, разбивающая пространство образов Ω на m непересекающихся классов Ω1, Ω2,..., Ω m. Индикаторная функция неизвестна наблюдателю. X– пространство наблюдений, воспринимаемых наблюдателем (пространство признаков). x (ω): Ω → X – функция, ставящая в соответствие каждому объекту ω точку x (ω) в пространстве признаков. Вектор x (ω) - это образ объекта, воспринимаемый наблюдателем. В пространстве признаков определены непересекающиеся множества точек Ki
Ω – объект распознавания (образ). g (ω):Ω →M, M = {1,2,..., m } – индикаторная функция, разбивающая пространство образов Ω на m непересекающихся классов Ω1, Ω2,..., Ω m. Индикаторная функция неизвестна наблюдателю. X– пространство наблюдений, воспринимаемых наблюдателем (пространство признаков). x (ω): Ω → X – функция, ставящая в соответствие каждому объекту ω точку x (ω) в пространстве признаков. Вектор x (ω) - это образ объекта, воспринимаемый наблюдателем. В пространстве признаков определены непересекающиеся множества точек Ki 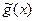 :
:  – решающее правило – оценка для g (ω) на основании x (ω), т.е.
– решающее правило – оценка для g (ω) на основании x (ω), т.е.  . Пусть x j= x( ωj ), j =1,2..., N – доступная наблюдателю информация о функциях g (ω) и x (ω), но сами эти функции наблюдателю неизвестны. Тогда (g j, x j), j 1,2..., N – есть множество прецедентов.
. Пусть x j= x( ωj ), j =1,2..., N – доступная наблюдателю информация о функциях g (ω) и x (ω), но сами эти функции наблюдателю неизвестны. Тогда (g j, x j), j 1,2..., N – есть множество прецедентов. .
.