
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии информативности признаковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При решении задач распознавания основным критерием (в том числе и для оценки информативности признаков) является риск потерь. Он основан на оценке вероятностей ошибок распознавания и их стоимости. Говорить об оценке вероятностей можно лишь в рамках статистического подхода, поэтому в данном разделе лучше применять критерий типа: доля контрольной (экзаменационной) выборки, распознанная неправильно. Мы уже упоминали о том, что объекты обучающей выборки не должны входить в контрольную выборку. В тех случаях, когда общая выборка невелика по объёму, деление её на две части весьма нежелательный шаг (ухудшится и качество обучения, и доверие к результатам контроля). Некоторые исследователи для компенсации этого недостатка применяют метод так называемого скользящего контроля. Он состоит в следующем. Все объекты, кроме одного, предъявляются в качестве обучающей выборки. Один объект, не участвовавший в обучении, предъявляется на контроль. Затем из общей выборки отбирается другой объект для контроля, по оставшейся части выборки осуществляется обучение. Такая процедура повторяется столько раз, сколько объектов в общей выборке. В таком случае вся выборка участвует и в обучении, и в контроле, но контрольные объекты не участвуют в обучении. Этот положительный эффект достигается ценой того, что обучение производится не один раз, как это было бы при наличии двух разных выборок (обучающей и контрольной) достаточно большого объёма, а столько раз, сколько объектов в общей выборке. Такой недостаток существенен, поскольку процедура обучения обычно достаточно сложна и её многократное повторение нежелательно. Если же данная процедура используется для отбора информативных признаков, то количество "обучений" нужно ещё умножить на количество сравниваемых между собой наборов признаков. Поэтому для оценки информативности признаков и решения иных задач часто используется не относительное число ошибок распознавания, а другие критерии, с ним связанные. В любом случае эти критерии выражают степень различимости объектов разных образов. Например, как это уже отмечалось при рассмотрении алгоритмов таксономии, отношение среднего расстояния между объектами разных образов к среднему расстоянию между объектами одного образа в ряде случаев оказывается весьма эффективным. Предлагается самостоятельно записать соответствующие вычислительные формулы, введя необходимые обозначения. При использовании подобных критериев контрольная выборка не нужна, но теряется взаимнооднозначная связь с количеством ошибок распознавания. Ясно, что среднее расстояние между объектами разных классов получается усреднением расстояний между всеми возможными парами объектов, принадлежащих разным классам. Если число классов велико и каждый из них представлен значительным количеством объектов, то процедура усреднения оказывается громоздкой. В этом случае можно воспользоваться усреднением расстояний между эталонами разных классов, а внутри классов – усреднением расстояний от объектов до эталона данного класса. Вполне понятно, что такое упрощение не всегда допустимо. Всё зависит от формы и взаимного расположения областей признакового пространства, в которых сосредоточены объекты разных классов. Метод потенциальных функций Название метода в определённой степени связано со следующей аналогией (для простоты будем считать, что распознаётся два образа). Представим себе, что объекты являются точками
Рис. 8. Иллюстрация синтеза потенциальной функции
Функцию, описывающую распределение электростатического потенциала в таком поле, можно использовать в качестве решающего правила (или для его построения). Если потенциал точки
Распознавание может осуществляться следующим способом. В точке При большом объёме обучающей выборки эти вычисления достаточно громоздки, и зачастую выгоднее вычислять не Выбор вида потенциальных функций – дело непростое. Например, если они очень быстро убывают с ростом расстояния, то можно добиться безошибочного разделения обучающих выборок. Однако при этом возникают определённые неприятности при распознавании неопознанных объектов (снижается достоверность принимаемого решения, возрастает зона неопределённости). При слишком "пологих" потенциальных функциях может необоснованно увеличиться количество ошибок распознавания, в том числе и на обучающих объектах. Определённые рекомендации в этом отношении можно получить, рассматривая метод потенциальных функций со статистических позиций (восстановление плотности распределения вероятностей Общий алгоритм применения метода потенциальных функций ¾ Рассчитываем признаки распознаваемого образа. ¾ Рассчитываем расстояния между эталонами и распознаваемым объектом, находя метрику между центром каждого из классов эталона, заданным в качестве исходных данных и вектором параметров, вычисленных для загруженного на форму образа. ¾ Находим потенциалы, создаваемые каждым из классов в той точке рецепторного пространства, где находится контур по формуле: ¾ Находим максимум из всех потенциалов ¾ Считаем, что объект относится к классу, потенциал которого максимален в точке пространства рецепторов, где расположен образ.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.7 (0.007 с.) |

 некоторого пространства
некоторого пространства 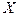 . В эти точки будем помещать заряды
. В эти точки будем помещать заряды  , если объект принадлежит образу
, если объект принадлежит образу  , и
, и  , если объект принадлежит образу
, если объект принадлежит образу  (рис. 8).
(рис. 8).
 – потенциальная функция, порождаемая одиночным объектом;
– потенциальная функция, порождаемая одиночным объектом; – суммарная потенциальная функция, порождённая обучающей последовательностью
– суммарная потенциальная функция, порождённая обучающей последовательностью , создаваемый единичным зарядом, находящимся в
, создаваемый единичным зарядом, находящимся в  , то общий потенциал в
, то общий потенциал в 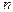 зарядами, равен
зарядами, равен
 и монотонно убывающая до нуля при
и монотонно убывающая до нуля при  .
. . Если он оказывается положительным, то объект относят к образу
. Если он оказывается положительным, то объект относят к образу  или разделяющей границы по выборке с использованием процедуры типа стохастической аппроксимации).
или разделяющей границы по выборке с использованием процедуры типа стохастической аппроксимации).



