Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия пирсона.Содержание книги
Поиск на нашем сайте
Задано эмпирическое распределение дискретной случайной величины X. Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона. Правило. Для того чтобы при уровне значимости а проверитьгипотезу о том, что случайная величина X распределена по законуПуассона, надо: 1. Найти по заданному эмпирическому распределению выборочнуюсреднюю дгв. 2. Принять в качестве оценки параметра А, распределения Пуассона выборочную среднюю X = Xj^. 3. Найти по формуле Пуассона (или по готовым таблицам) вероятности Pi появления ровно i событий в п испытаниях (i = 0,1,2,..., г, где г — максимальное число наблюдавшихся событий; п — объем выборки / 4. Найти теоретические частоты по формуле п'^-п- Pi. 5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-2, где s — число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то s — число оставшихся групп выборки после объединения частот).
42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта. С помощью критериев, основан на сравнении дисперсии и на f(-статистики Фишера) Постановка задачи: Для задачь к выборок (R-выборов)
Пусть на результирующ. признак оказывают влияние как ф-ых признаков
Схема проверки 1) выделяются гипотезы Но: 2) несмещен точечные оценки ген. дисперс. ур-ний 3) находится оценка ген диспер. всех ур. 4) находится экспер. знач. параметра 5) Находит эмперич. зн. критерия Бартл. 6) определяется кріт зн. статистики критерия Бартл.
7) 43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа. Значимость фактора на результат признака Схема проверки:
1) выдвигаются гипотезы Но=влияние фактора на результат не значима, т.е. случ. Н1: значимо, т.е. не случайно. 2) находится ∑результатов наблюдения на каждом из ур. i=1…k 3)находится ∑ результатов не всех ур. вместе 4) Находится ∑ квадратов наблюдений 5) Находится ср. знач. ур-нь ∑квадр. 6) находится обяз. ср. ∑ квадратов
7)находится несмещен. точечная общ. дисперсии всех ур. 8) -//- несмещ. течечн. оценка ф-рах 9) экспер. зн. статистики критерия 10) опред. крит. зн. статистики критерия
44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа. Проверка стат. гипотез с помощью дисперсион. анализа 1)Проверка гипотезы о равенстве ср. значений признака в ГС на всех ур-ях Схема проверки 1) Формир-е основн и альтерн. ей гипотез Но: х1=х2… = 2) находятся несмещен. течечн. оценки ген. ср. каждого 3) находится несмещен. точечная оценка общ. ср. ген зн. всех ур. вместе 4) Расходится внутригрупповая ∑ квадратов отклонения экспер. данных ур. от уравн. ср. знач-й 5) 6) находится экспер. зн. статист. критер 7) находит зн. стат. 8)
Выборочный парный коэффициент линейной корреляции, его свойства и значимость. Коэффициент детерминации, его свойства и интерпретация. Выбороч. кар. коэф. линейн. кор-ции м/у признаками(Х,У) наз. величина обозн.
Коэф. кор-ции показыв. ст зависимость признаков след. образом. 1)r=o 2) rϵ(0;0.1]-м/у ХиУ оч. слабая кор-я 3) rϵ(0.1; 0.3] –слаб. кор-я связь 4) rϵ(0.3;0.7] –умерен. -//- 5) rϵ(j.7;0.99]-сильная -//- 6)r=1-совершенная связь. Св-ва коэф-та кор-ции: 1) -1 2) r= Значимость линейн. коэф-та кор-ции в ГС: 1) издается уравнение значимость альфа 2) Выдвигается основ и альтернативн. ей гипетезы. Но:r в ГС н/з 3) Находится эксперимент. зн. стат. крит. 4) Находится крит. зн. Ѳкр, Ткр Ѳкр=t(альфа;υ)=t(альфа;n -2) 5)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.100 (0.01 с.) |

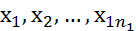 i-I
i-I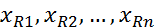
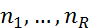 -извлечен из распределений ГС требует. проверить гипотезу о равенстве ГС Но=
-извлечен из распределений ГС требует. проверить гипотезу о равенстве ГС Но= 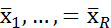 или
или 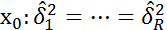 или о значимости влияния ф-ра из 2 уровней на результирующ. признак ГС.
или о значимости влияния ф-ра из 2 уровней на результирующ. признак ГС.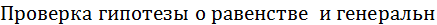 . дисперсий всех ф-ов (всех ур.) по крит. Бартл.
. дисперсий всех ф-ов (всех ур.) по крит. Бартл.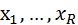 эксперементальн. данные R-тых представлены табл-й
эксперементальн. данные R-тых представлены табл-й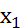
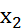
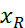
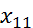
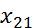
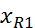
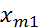
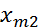
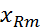
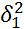 =…=
=…= 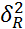 (генеральн. диспесии каждого из ур.=м/у собой)
(генеральн. диспесии каждого из ур.=м/у собой) 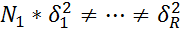
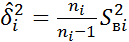 , гдне i=1-R
, гдне i=1-R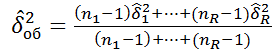
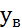 статистики критерия Барл.
статистики критерия Барл. 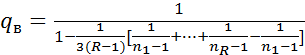
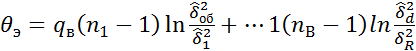
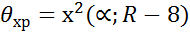 ,
, 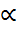 -задан. ур. значимости
-задан. ур. значимости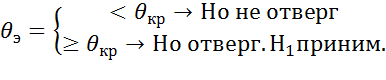
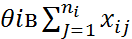
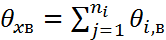
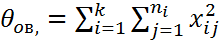

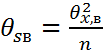 n=n+…+
n=n+…+ 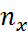
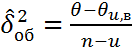
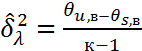
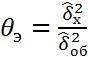
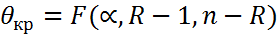 11)
11) 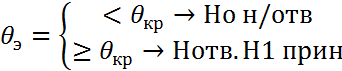
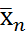 (ген. ср. на всех одинаковы)
(ген. ср. на всех одинаковы)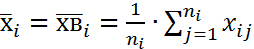 i=1…k
i=1…k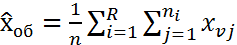
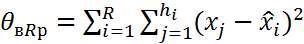
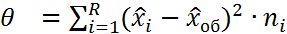
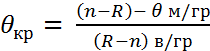
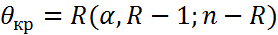
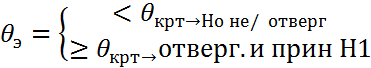
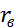 и опр. анал. выр.
и опр. анал. выр. 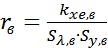 где
где 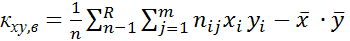 (корреляц. момент)
(корреляц. момент)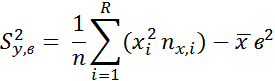
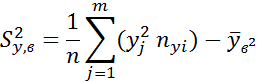
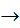 X иYне кор. связи
X иYне кор. связи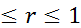
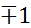 , то м/у признаками сущ. линейная формульная зависимость. 3)r<0, то из с возрастанием зн. одного из признаков зн. ур. в сред. убывают.
, то м/у признаками сущ. линейная формульная зависимость. 3)r<0, то из с возрастанием зн. одного из признаков зн. ур. в сред. убывают.