
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи теории вероятностей. Пространство элементарных событий.Содержание книги
Поиск на нашем сайте Предмет и задачи теории вероятностей. Пространство элементарных событий. Под экспериментом понимается процесс протикающ. при определенном усл. в результате которого набл. то, или иное явление фиксируется той или иной результат. Определение 1. единичное выполнение эксперимента(опыта) наз. испытание. В теории вероятности рассматривается как результат испытаний, а термин испытание иногда заменяется термином наблюдение, опыт, измерения. Определение2. Любой исход независимо от его значимости может произойти, или не произойти в результате эксперимента (опыта) наз.(СС)-случ. событием, или просто событием. Пр-во элементарн событ. Определение1. Элементами событ.(эксперимент исходами соб-я) наз. возможно. взаимоисп. друг друга исходы данного эксперимента. Это те события кто-е нельзя разложить на более простые. Элементарные события обозн. w - амего с индексами(w1,w2,w3 и т.ед.), или А1,А2,… или В1,В2 и др. Определение2. Совокупность всех взаимоисп. исходов экспермим. (всех элемент-х событий) наз. пространство элемент. событий данного эксперимента и обозн прописн. греч. буквой Ω- амега конечно, или счетно, тогда СС ожно рассматривать подмножество пространство элемент. событий. Ω= Определение3. Событие наз. сложный если можно угадать 2 элемент. события таких, что из существ-я каждого из них в отдельности следует и существ-е определенного СС. Это то событие кто-е состоит из нескольких элементарных А=
Случайные события и их классификация. Операции над событиями. Определение1. СС наз. достоверным если в результате эксперимента оно обязательно попадает. Достов. соб-е обозн. Ω-амега. Определение2. Невозможн. наз. такое СС кат-е в результате экспреим. никогда не произойдет. Невозможное событие обозн. Ø Определение3. Два события совместные в данн. эксперим. если в нем они могут произойти одновр. и наз. не совместные, если их совместно. наступление исключительно Опреация над событиями Опред.1. суммой А и В-событие, состоящее в том, что произойдет хотя бы 1 из них. (А+В или А и В) Определение2. А и В- событие, состоящ. в том, что произойдет оба данных события вместе (А ٠ В или АВ,) Определение3. Разностью 2-х событий А и В наз. событие кот-е происходит тогда когда происходит событие А и не происходит событие В и обозн. А-В или А\В (А без. В)
Частота появления случайного события и ее свойства. Ч исло m наступлений соб. А в n эксп. наз. абсолютной частотой наступления А, а отнош числа эксп m, в кот происходило А к числу всех проведенных эксп n – относ частота или частота наступления А. w(A): w/A=m/n. Свойства 1. 0<=w(A)<=1, где А-пр 2. w(дост.)=1 3. w(невозм)=0 4. w(A+B)=w(A)+w(B), А и В несовместимые
Вероятность случайного события и её свойства Определение1: (статистическое) Вероятностью случ. Событ. А назыв. постоянная величина обозначаемая Р(А) около которой группируются частоты данного события по мере увеличения числа эксперимента: Р(А) ~ w(A) =m/n m- число экспериментов в котором наступило событие А, n- число всех провед. эксперим. Опред2: Благоприятствующая к событ. исхода эксперимента, назыв. элемент. исходы экспер. При которых данное событие наступает. Определение3: (классическое)вероятностью наступл.события А назыв. величина обознач Р(А) и определяемое, как отношение числа благоприятств. событ. А исходов экспериментов к числу всех исходов данного экспер. Р(А) =m/n m- число благопр. событ. А исходов экспер. n- число всех исходов эксп. Свойства вероятности: 1) 0 ≤ Р(А) ≤ 1, А- произ.соб. 3) Р(ᴓ) =0, ᴓ - невозм. 2) Р(Ω) = 1, Ω - достоверн. 4) Р(А)+Р(Ā) = 1, А и Ā- противоп. событ. Определение4: (аксиоматическое) Вероятностью наступления событ. А назыв. числовая функция обознач. Р(А) удовлетвор. след. аксиомам: 3 и 4 свайства.Следствие из 4 аксиомы: Р(А) = 1 – Р(Ā) или Р(Ā) = 1 – Р(А). Геометрический подход: Предположим, что число равновозм. Экспер. бесконечно и несчётно, будем интерпретировать элемент.соб. как точки на прямой, на плоскости или в простр. Когда множество элем. событ. Ω представл. собой подмножества соотв. Пространства котор.будем предполаг. Огранич. И измеримым. Т.е. имеющ. Геометрическую меру (длину, площадь или объём). Определение5: Геометр.Вероятностью или вероятн. Наступл.случ.события назыв. величина обознач. Р(А) и равная отношению геометр.меры(S,P или V) благоприятств. данному событию к геометр. мере всего множества возможн.эксперим.: Р(А)=mesA/mesΩ, где геометр.мера, те Р(А)= L(A)/L(Ω)=S(A)/S(Ω)=V(A)/V(Ω)
Схема проверки 1) выделяются гипотезы Но: 2) несмещен точечные оценки ген. дисперс. ур-ний 3) находится оценка ген диспер. всех ур. 4) находится экспер. знач. параметра 5) Находит эмперич. зн. критерия Бартл. 6) определяется кріт зн. статистики критерия Бартл.
7) 43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа. Значимость фактора на результат признака Схема проверки: 1) выдвигаются гипотезы Но=влияние фактора на результат не значима, т.е. случ. Н1: значимо, т.е. не случайно. 2) находится ∑результатов наблюдения на каждом из ур. i=1…k 3)находится ∑ результатов не всех ур. вместе 4) Находится ∑ квадратов наблюдений 5) Находится ср. знач. ур-нь ∑квадр. 6) находится обяз. ср. ∑ квадратов
7)находится несмещен. точечная общ. дисперсии всех ур. 8) -//- несмещ. течечн. оценка ф-рах 9) экспер. зн. статистики критерия 10) опред. крит. зн. статистики критерия
44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа. Проверка стат. гипотез с помощью дисперсион. анализа 1)Проверка гипотезы о равенстве ср. значений признака в ГС на всех ур-ях Схема проверки 1) Формир-е основн и альтерн. ей гипотез Но: х1=х2… = 2) находятся несмещен. течечн. оценки ген. ср. каждого 3) находится несмещен. точечная оценка общ. ср. ген зн. всех ур. вместе 4) Расходится внутригрупповая ∑ квадратов отклонения экспер. данных ур. от уравн. ср. знач-й 5) 6) находится экспер. зн. статист. критер 7) находит зн. стат. 8)
Основные и не основные числовые характеристики случайной величины, их свойства и способы их вычисления. (ЗР и ЧХ СВ) Мат ожидание СВ х наз-ся величина,обознач М(Х) и определяется неравенством mX Опред. 1 Мат ожидание характеризует среднее (центральное) значение СВ, определяющ. Положение кривой плотности вер-сти вдоль оси ОХ в знач. СВ. При увеличении значения СВ, кривая вер-сти сдвигается в право. Определение2. Дисперсией СВ наз-ся мат ожидание кватдрата отклонения СВХ от своего мат ожидания, обознач. D(X) или DX DX=[(x-mx)2] Дисперсия СВ опред одним из аналитич выражений DX Дисперсия характеризует степень разброса возможных значений СВ вокруг своего мат ожидания
Св-ва мат ожидания 1. M(C) =C 2. М(СХ)=СМ(Х) 3. М(Х+У)=М(Х)+М(У) 4. М(Х+С)=М(Х)+С Св-ва дисперсии 1. D(C)=0, Спр 2. D(CX)=C2D(X) 3. D(X+Y)=D(X)+D(Y), X,Y – независим. СВ 4. D(X+C)=D(X) 5. D(XY)=DxDy+Dxmy2+Dymx2, X,Y – независим. СВ 6. D(X)≥0
Опред.3. Средним квадратич отклонением СВ Х наз-ся величина,обознач как СИГМА Х (6 с продолговатым хвостом) и определяется как корень квадратный из дисперсии(D(X)) Среднее кВ.отклонение характеризующееся рассеив. осн. массы возможн. знач СВХ, относительно мат ожидания этой СВ НЕОСНОВНЫЕ ЧХ СВ Опред 1- Начальным моментом k-того порядка СВ Х наз-ся величина,обознач НЮ С ИНДЕКСОМ K(как v) НЮk Опред2- Ценртральным моментом k-того порядка вел Х наз-ся вел НЮk Mk Следствия из опред 1. НЮ= 2. 3 Опред3 - Коэфф. ассиметрии (скошенности) СВХ наз-ся вел ax и определяется Примечание: если ax=0,то график кривой распределения симметричен относительно мат ожидания СВ Опред 4- Коэф. Эксцесса (островершинности) СВ Х обознач ех и опред равенством
Примечания: 1 если ех больше 0 то крив распред СВ островершинна 2 если ех меньше 0 то крив распред СВ плосковершинна Опред5 модой СВХ наз-ся наиболее вероятное значение данной СВ, обознач Мох (это то знач СВ для кот вер-сть pi в случае ДСВ или плотность вер-сти f(x) НСВ достигает макс. Знач. Опред 6- медианой СВХ наз-ся величина, обознач Мех и равная серединному возможному знач в случае ДСВ или тому, знач СВ,для кот выполн условие P`(x<Me,x)=P(X> Me,x) в случае НСВ. Опред 7- Квантилью СВХ наз-ся величина, обознач Хp для кот справедливо равенство P(X<Xp)=F(Xp)=P
Предмет и задачи теории вероятностей. Пространство элементарных событий. Под экспериментом понимается процесс протикающ. при определенном усл. в результате которого набл. то, или иное явление фиксируется той или иной результат. Определение 1. единичное выполнение эксперимента(опыта) наз. испытание. В теории вероятности рассматривается как результат испытаний, а термин испытание иногда заменяется термином наблюдение, опыт, измерения. Определение2. Любой исход независимо от его значимости может произойти, или не произойти в результате эксперимента (опыта) наз.(СС)-случ. событием, или просто событием. Пр-во элементарн событ. Определение1. Элементами событ.(эксперимент исходами соб-я) наз. возможно. взаимоисп. друг друга исходы данного эксперимента. Это те события кто-е нельзя разложить на более простые. Элементарные события обозн. w - амего с индексами(w1,w2,w3 и т.ед.), или А1,А2,… или В1,В2 и др. Определение2. Совокупность всех взаимоисп. исходов экспермим. (всех элемент-х событий) наз. пространство элемент. событий данного эксперимента и обозн прописн. греч. буквой Ω- амега конечно, или счетно, тогда СС ожно рассматривать подмножество пространство элемент. событий. Ω= Определение3. Событие наз. сложный если можно угадать 2 элемент. события таких, что из существ-я каждого из них в отдельности следует и существ-е определенного СС. Это то событие кто-е состоит из нескольких элементарных А=
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.27 (0.006 с.) |

 - пространство эл. событий.
- пространство эл. событий.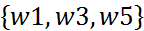 следов-но соб-е А сложное.
следов-но соб-е А сложное.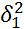 =…=
=…= 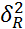 (генеральн. диспесии каждого из ур.=м/у собой)
(генеральн. диспесии каждого из ур.=м/у собой) 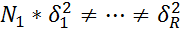
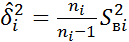 , гдне i=1-R
, гдне i=1-R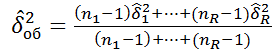
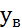 статистики критерия Барл.
статистики критерия Барл. 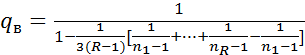
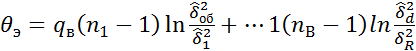
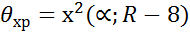 ,
, 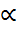 -задан. ур. значимости
-задан. ур. значимости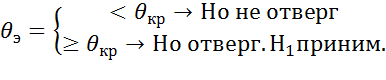
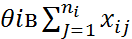
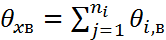
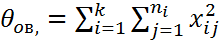

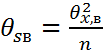 n=n+…+
n=n+…+ 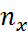
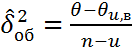
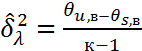
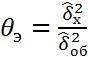
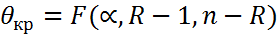 11)
11) 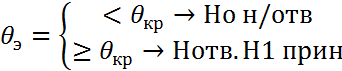
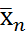 (ген. ср. на всех одинаковы)
(ген. ср. на всех одинаковы)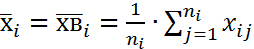 i=1…k
i=1…k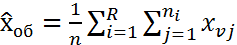
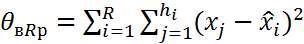
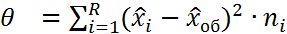
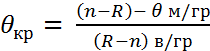
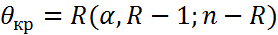
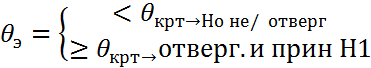
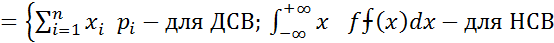
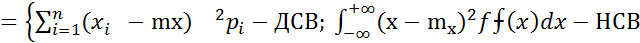
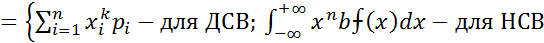
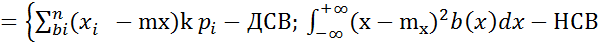
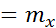
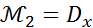
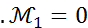
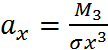
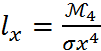 данной СВ Х
данной СВ Х


