Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.

Опред.1 Доверительным интервалом (интервальной оценкой) для неизвестного параметра Ө ГС наз. интервал (Ө₁, Ө₂), содержащ. неизвестное значение данного параметра Ө с вероятностью ɣ: P(Ө₁< Ө< Ө₂) = ɣ.

Опред.2 Число гамма ɣ называется доверительной вероятностью или уравнением надежности, а число α = 1- ɣ называется уравнением значимости ɣ.

Опред.3 Статистики Ө₁= Ө₁ (х₁, …, х_n) и Ө₂= Ө₂ (х₁, …, х_n), определяемые по экспериментальным данным, называется нижней и верхней границами доверительного интервала.

При увеличении числа выборки n длина доверительного интервала уменьшается, а при приближении доверительной вероятности ɣ→1 – длина доверительного интервала увеличивается.

Опред.4 Предельной ошибкой выборки называется наибольшее значение отклонения точечной оценки параметра от его истинного значения.

Доверительный интервал для генерального среднего значения признака.

Пусть признак Х нормально распределен в ГС и пусть х₁, …, х_n – его выборочные значения. (X?N(m_x, ᵟx). Предположим, что задана доверительная вероятность ɣ, тогда доверительный интервал для генерального среднего значения признака определяется формулой:

где

28. Доверительный интервал для среднего квадратичного отклонения. Требуется найти доверительные интервалы, покрывающие параметры Dи s с заданной надежностью g. Потребуем выполнения соотношения . Раскроем модуль и получим двойное неравенство: . Преобразуем: . Обозначим d/s = q (величина q находится по "Таблице значений q"и зависит от надежности и объема выборки), тогда доверительный интервал для оценки генерального среднего квадратического отклонения имеет вид: . Замечание: Так как s >0, то если q >1, левая граница интервала равна 0: 0< s < s (1 + q).

 

29.Понятие статистической гипотезы. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Простая гипотеза однозначно характеризует параметр распределения случайной величины. Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, здесь указывается некоторая область вероятных значений параметра. Нулевая гипотеза (Но) — это гипотеза о том, что есть две совокупности, которые сравниваются по одному или нескольким признакам, не отличаются. Параметрическая гипотеза — это гипотеза о параметрах генеральной совокупности. Непараметрическая гипотеза — это гипотеза о параметрах распределения. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. статистический критерий определяется статистикой T и критическим множеством , которое зависит от уровня значимости . Мощность критерия вычисляется по формуле (1 − β). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода. уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, F –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).

Пусть даны выборка X = () из неизвестного совместного распределения , и семейство статистических гипотез . Тогда статистическим критерием называется функция, устанавливающая соответствие между наблюдаемыми величинами и возможными гипотезами: f: .

Таким образом каждой реализации выборки статистический критерий сопоставляет наиболее подходящую с точки зрения этого критерия гипотезу о распределении, породившем данную реализацию.

Критерий Пирсона Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H ₀ о том, что эта случайная величина подчиняется закону распределения F (x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F ^* (x) исследуемой случайной величины. Сравнение эмпирического распределения F ^* (x) и теоретического (или, точнее было бы сказать, гипотетического - т.е. соответствующего гипотезе H ₀) распределения F (x) производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона. Для проверки критерия вводится статистика:

;

где — предполагаемая вероятность попадения в i -й интервал, 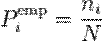— соответствующее эмпирическое значение, n_i — число элементов выборки из i -го интервала, N — полный объём выборки. Также используется расчет критерия по частоте, тогда:

где V_i - частота попадания значений в интервал. Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ².