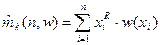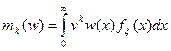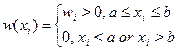Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий Вилкоксона-Манна-УитниСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Этот критерий предназначен для проверки однородности двух генеральных совокупностей, понимаемой в смысле отсутствия различий в значениях параметров местоположений (медиан, средних значений) соответствующих распределений. Мы располагаем выборками, извлеченными из двух генеральных совокупностей (l=2). Пронумеруем эти выборки, так чтобы обеспечить выполнение неравенства n1 Критическая статистика описываемого критерия имеет вид: (2) Следующее правило проверки гипотезы: 1) По заданному уровню значимости критерия a с помощью таблиц квантилей (процентных точек) стандартного нормального распределения определяем квантиль 2) Вычисляем стандартизированное значение критической статистики g
где значение g вычислено по формуле. 3) Если окажется, что |gст|>U1-a/2 В условиях справедливости проверяемой гипотезы статистика ведет себя как нормально распределенная случайная величина с параметрами: a=1/2n1(n1+n2+1) s2=1/12n1n2(n1+n2) При этом сходимость к нормальному распределению очень быстрая: оно уже эффективно работает при n1>8. Взвешивание выборочных данных х1,…,хn. В общем случае наблюдению хi приписывается вес wi ³ 0, который определяется как некоторая функция от его текущего значения. Обычно wi подчиняют условию нормировки
Под w понимается вектор весов (w(x1)…w(xn)) в выражении для выборочных моментов и функция со значениями w(x) в выражении для теоретических моментов. Если имеют дело с результатами наблюдения одномерной случайной величины х1…хn, то часто вес наблюдения хi определяют в зависимости от его порядкового номера в упорядоченном (по возрастанию) ряду наблюдений, то есть располагают наблюдения в вариационный ряд х1,х2,…,хn и каждому члену вариационного ряда хi ставят в соответствие некоторый вес wi. Цензурирование выборки. Этот приём заключается в приписывании ряду «хвостовых» членов вариационного ряда нулевых весов, а остальным одинаковых положительных. Если приписывание нулевых весов производится по признаку выхода текущих значений наблюдений за пределы заданного диапазона [a;b], то есть:
то говорят о цензурировании первого типа. Очевидно, в случае число u оставшихся в рассмотрении наблюдений есть величина случайная (u < n). Если же нулевые веса приписываются фиксированной доле a крайних малых значений и фиксированной доле b крайних больших значений, то говорят, что производится цензурирование второго типа уровня (a и b). В этом случае число u оставшихся в рассмотрении наблюдений является величиной, заранее заданной и равной, в частности n(1-a-b). Исследователь может прибегнуть к цензурированию вынужденно или добровольно. Вынужденное цензурирование обусловлено соответствующими условиями эксперимента: например, мы ставим на разрушающие испытания n изделий, но можем проводить эксперимент в течение ограниченного времени Т. Очевидно, мы будем вынуждены произвести в данном случае одностороннее цензурирование первого типа, при котором из дальнейшего рассмотрения исключаются точные значения долговечностей (времени до разрушения) всех тех изделий, которые не разрушились за время Т. С другой стороны, в классе оценок, построенных по цензурированным выборкам, часто можно найти оценки, хотя и не являющиеся наилучшими в рамках генеральной совокупности определённого типа, но обладающие выгодными свойствами устойчивости своих хороших качеств по отношению к тем или иным отклонениям от априорных допущений. Урезание распределения. Это понятие связано с ситуациями, когда исследуемый признак x не может быть наблюдаем в какой-либо области его возможных значений. Так, например, если мы исследуем распределение семей по доходу, то по условиям выборочного обследования лишены возможности наблюдать семьи со средне нулевым доходом, меньше некоторого заданного уровня a (тыс. руб.), то в подобных случаях говорят, что распределение урезано слева в точке a. В отличие от цензурированных выборок в выборках из урезанных распределений мы не имеем возможности оценить даже доли наблюдений, располагающихся за пределами порога урезания.
Задания для самостоятельного решения.
1. Аудиторская фирма хочет проконтролировать состояние счетов одного из коммерческих банков. Для этого случайно отбираются 50 счетов. По 20 счетам из 50 отобранных имело место движение денежных средств в течении месяца. Постройте 99% доверительный интервал, оценивающий долю счетов в генеральной совокупности, по которым имело место движение денежных средств в течении месяца. 2. Туристическую фирму крупного курортного города интересует связь между числом отпускников, остановившихся в отелях и расходами на рекламу отелей. Взято случайное число отелей - 6, сходных по размеру. Была собрана следующая информация за текущий сезон:
А). Требуется определить коэффициенты корреляции и детерминации. Б). Построить модель парной линейной регрессии. В). Полученное уравнение регрессии использовать для прогноза. В частности, пусть отель 7 тратит на рекламу 5000 ф.ст. Определить возможное количество посетителей. 3. Имеются данные о годовой мощности предприятий цементной промышленности в 1996 г.
А) Постройте гистограмму, кумуляту. Б) Рассчитайте среднюю мощность предприятий. В) Найдите дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты, сделайте выводы.
4. Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, методом случайной бесповторной выборки отобрано 30. По данным этой выборки установлено, что средний пробег автомобиля в течение месяца составляет 1 342 км со стандартным отклонением 227 км. Считая пробег автомобиля случайной величиной, распределенной по нормальному закону, найдите 95%-й доверительный интервал, оценивающий средний пробег автомобилей всего парка в течение месяца.
5. С помощью собственно-случайного повторного отбора руководство фирмы провело выборочное обследование 900 своих служащих. Средний стаж их работы в фирме равен 8,70 года, а среднее квадратическое (стандартное) отклонение — 2,70 года. Среди обследованных оказалось 270 женщин. Считая стаж работы служащих фирмы распределенным по нормальному закону, определите: а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих фирмы; б) с вероятностью 0,90 доверительный интервал, накрывающий неизвестную долю женщин во всем коллективе фирмы.
6. Владелец автостоянки опасается обмана со стороны своих служащих (охраны автостоянки). В течение года (365 дней) владельцем авто стоянки проведено 40 проверок. По данным проверок среднее число автомобилей, оставляемых на ночь на охрану, составило 400 единиц, а среднее квадратическое (стандартное) отклонение их числа — 10 автомобилей. Считая отбор собственно-случайным, с вероятностью 0,99 оцените с помощью доверительного интервала истинное среднее число автомобилей, оставляемых на ночь на охрану. Обоснованы ли опасения владельца автостоянки, если по отчетности охранников среднее число автомобилей, оставляемых на ночь на охрану, составляет 395 автомобилей?
7. По данным таблицы исследуйте зависимость между доходами семей Х (тыс. руб) и их расходами на потребление у.
1. Определите коэффициенты корреляции и детерминации. Объясните полученные результаты. 2. Постройте уравнение регрессии. 3. Постройте интервальные оценки параметров уравнения регрессии. 8. Вычислите коэффициент ассоциации для следующих данных:
9. Рассчитайте значение коэффициента λ-Гутмана:
10. Постройте систему рангов для следующих признаков:
Тестовые задания 1. Пространственные данные характеризуются: - большим количеством единиц наблюдения, сведения о которых относятся к одному интервалу времени; - большим количеством единиц наблюдения, сведения о которых относятся к одному моменту времени; - одной единицей наблюдения, сведения о которой относятся к различным интервалам времени.
2. По характеру вариации признаки могут быть: - моментными; -непрерывными; - альтернативными; - дискретными; - интервальными. 3. Качественные признаки могут быть измерены с помощью: - порядковой шкалы; - номинальной шкалы; -шкалы интервалов; - шкалы отношений. (несколько вариантов ответа)
4. Какое значение примет коэффициент ассоциации Юла, если хотя бы одна клетка таблицы сопряженности 2х2 равна 0: - 1; - 0; -[0;1].
5. Чем меньше предельная ошибка простой случайной выборки, тем ее численность: - больше; - меньше; - приведенный параметр не оказывает влияния на объем выборки.
6. Панельные данные характеризуются: - большим количеством единиц наблюдения, сведения о которых относятся к одному интервалу времени; - большим количеством единиц наблюдения, сведения о которых относятся к одному моменту времени; - одной единицей наблюдения, сведения о которой относятся к различным интервалам времени.
7. По отношению ко времени признаки бывают: - моментными; -непрерывными; - периодическими; - дискретными; - интервальными. (несколько вариантов ответа)
8. Способ основного массива относится к наблюдению: - сплошному; -несплошному; - монографическому.
9. Какой из типов шкал предполагает возможность упорядочения объектов по степени выраженности рассматриваемых свойств: - порядковая шкала; -шкала интервалов; - шкала отношений.
10. Значение коэффициента контингенции лежат в интервале: - -1;1 - 0; 1 - -1;0
11. При каком виде наблюдения подробно описываются отдельные единицы совокупности с целью их углубленного изучения: - способе основного массива; - выборочном; - монографическом.
12. Для использования меры связей λ- Гутмана необходимо, чтобы среди рассматриваемых переменных была хотя бы одна: -номинальная; - порядковая; - номинальная и недихотомическая
13. Если при построении таблицы статистическая совокупность разделяется на отдельные группы по какому-либо одному признаку, то таблица будет: - простая; - групповая; - комбинационная.
14. При совпадающих ранжировках коэффициент ранговой корреляции Спирмена равен: -1; -0; - -1.
15. Если при построении таблицы статистическая совокупность разделяется на отдельные группы одновременно по нескольким признакам, то таблица будет: - простая; - групповая; - комбинационная.
16. Программа статистического наблюдения включает: - объект наблюдения, территорию проведения наблюдения, критическую дату, признаки, подлежащие регистрации; - признаки, подлежащие регистрации; - объект наблюдения и территорию проведения наблюдения.
17. По отношению к характеризуемому объекту признаки могут быть: -описательные; - первичные; -прямые; -количественные; - косвенные. (Несколько вариантов ответа)
18.Какой из способов сбора данных может быть описан следующим образом: статистические или другие органы рассылают специально разработанные бланки и инструкции по их заполнению отдельным организациям или специально отобранным лицам, давшим согласие периодически их заполнять и присылать соответствующему органу в установленные сроки. - экспедиционный; -корреспондентский; -саморегистрация.
19. Из перечисленных ниже коэффициентов для четырехпольной таблицы сопряженности могут использоваться: - коэффициент конкордации; - коэффициент контингенции; - коэффициент ранговой корреляции Спирмена; - коэффициент ассоциации; - показатель λ-Гутмана. (Несколько вариантов ответа)
20. Если значение коэффициента ранговой корреляции Спирмена составляет 0,98, то можно сделать вывод, что: - ранжировки имеют совпадающие упорядочения сильной степени согласованности; - ранжировки имеют противоположные упорядочения сильной степени согласованности; - ранжировки имеют совпадающие упорядочения средней степени согласованности; - ранжировки не являются согласованными.
21. Какая из шкал предполагает наличие единицы отсчета и масштаба: - порядковая шкала; -шкала интервалов; - шкала отношений.
22. Если величина υ в коэффициенте ранговой корреляции Кэндалла равна 0, то его значение будет: -1; -0; - -1.
23. Если при проведении группировки проводится одновременная классификация по комплексу признаков, то группировка: - комбинационная; - многомерная; - типологическая.
24. К какой мере информации относится энтропия: - семантическая; -синтаксическая; - прагматическая.
25. Для определения характеристики структуры исследуемой совокупности проводится группировка: - комбинационная; - многомерная; - типологическая.
Глоссарий.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.013 с.) |

 n2. Объединим выборки и по объединненой выборке объема n1+n2 построим общий вариационный ряд.
n2. Объединим выборки и по объединненой выборке объема n1+n2 построим общий вариационный ряд.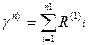 и носит название суммы рангов.
и носит название суммы рангов.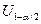 уровня 1-a/2 (или 100a/2% точку стандартного нормального распределения.
уровня 1-a/2 (или 100a/2% точку стандартного нормального распределения.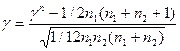 ,
, или |ga/2|>U1-a/2 , то проверяемую гипотезу следует отвергнуть (и соответственно принять при всех других значения стандартизированной критической статистики
или |ga/2|>U1-a/2 , то проверяемую гипотезу следует отвергнуть (и соответственно принять при всех других значения стандартизированной критической статистики 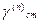 .
.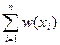
 1
1