
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многофункциональные статистические критерии.Содержание книги Поиск на нашем сайте
Многофункциональные статистические критерии - это критерии, которые могут использоваться по отношению к самым разнообразным | данным, выборкам и задачам. Это означает, что данные могут быть представлены в любой шкале, начиная от номинативной (шкалы наименований). Это означает также, что выборки могут быть как независимыми, так и "связанными", то есть мы можем с помощью многофункциональных критериев сравнивать и разные выборки испытуемых, и показатели одной и той же выборки, измеренные в разных условиях. Нижние границы выборок - 5 наблюдений, но возможно применение критериев и по отношению к выборкам с п=2, с некоторыми оговорками (см. разделы "Ограничения критерия φ*" и "Ограничения биномиального критерия m”) Верхняя граница выборок задана только в биномиальном критерии - 50 человек. В критерии φ* Фишера верхней границы не существует - выборки могут быть сколь угодно большими. Многофункциональные критерии позволяют решать задачи сопоставления уровней исследуемого признака, сдвигов в значениях исследуемого признака и сравнения распределений. К числу многофункциональных критериев в полной мере относится критерий φ* Фишера (угловое преобразование Фишера) и, с некоторыми оговорками - биномиальный критерий m. Назначение критерия φ* Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Описание критерия Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол ф, а меньшей доле - меньший угол, но соотношения здесь не линейные: где Р - процентная доля, выраженная в долях единицы. Гипотезы H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2. H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2. Метод ранговой корреляции. Для оценки тесноты связи между признаками, оцененными при помощи порядковой (ранговой) шкалы используется метод ранговой корреляции. Естественно, что этот метод применим также для признаков, оцененных по интервальной или относительной шкале. Для оценки тесноты связи используется коэффициент ранговой корреляции, который по смыслу идентичен линейному коэффициенту корреляции. Чаще всего при использовании этого метода вычисляется ранговый коэффициент Спирмена
где
Коэффициент корреляции рангов Кендэла
Коэффициент Кендэла всегда меньше по значению, чем коэффициент Спирмена и для достаточно больших совокупностей Критическое значение коэффициента Спирмена При ранжировании иногда значения признаков двух или большего числа объектов равны между собой. Такие объекты называются связанными и им приписываются одинаковые средние ранги. Средние ранги равны среднему арифметическому номеров этих объектов в общем списке проранжированных объектов. Дл расчета коэффициента Спирмена в случае наличия связанных рангов существует специальная формула, но приблизительная оценка может быть получена и по общей формуле. Дисперсионный анализ. Дисперсионный анализ – анализ изменчивости признака под влиянием какой-либо контролируемой переменной (переменных) или фактора (факторов). Автор данного метода статистического расчета Р.А. Фишер. Задача дисперсионного анализа состоит в том, что определить соотношение случайной вариативности признаков, с вариативностью обусловленной действием каждой независимости переменной или взаимодействием совокупности независимых переменных. Другими словами определить отличается ли влияние независимых переменных от любого другого случайного влияния. Дисперсионный анализ построен на исследовании особенностей распределения признака, поэтому является параметрическим. Для расчета дисперсионного анализа используют критерий F. F - критерий Фишера вычисляется по формуле:
где Если вычисленное значение критерия F больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Число степеней свободы числителя определяется по формуле:
где Число степеней свободы знаменателя определяется по формуле:
где
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.008 с.) |

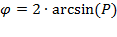
 либо ранговый коэффициент Кендэла
либо ранговый коэффициент Кендэла 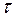 . Расчет коэффициента Спирмена основан на фиксации разности рангов двух параллельных рядов наблюдений – ряда признака
. Расчет коэффициента Спирмена основан на фиксации разности рангов двух параллельных рядов наблюдений – ряда признака 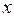 и рада признака
и рада признака 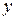 :
: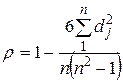 ,
,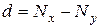 , то есть разность рангов каждой пары значений
, то есть разность рангов каждой пары значений  - число наблюдений.
- число наблюдений.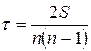 , где
, где 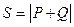 .
.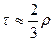 . Чем ближе коэффициенты к единице (по модулю), тем теснее зависимость, а близость к нулю означает отсутствие связи или весьма малую зависимость.
. Чем ближе коэффициенты к единице (по модулю), тем теснее зависимость, а близость к нулю означает отсутствие связи или весьма малую зависимость.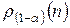 определяется по таблице в зависимости от уровня значимости
определяется по таблице в зависимости от уровня значимости  и числа наблюдений
и числа наблюдений 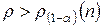 , то существенность связи доказана с вероятностью
, то существенность связи доказана с вероятностью  .
. ,
,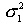 - большая дисперсия,
- большая дисперсия, 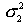 - меньшая дисперсия.
- меньшая дисперсия. ,
,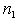 - число вариант для большей дисперсии.
- число вариант для большей дисперсии. ,
,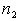 - число вариант для меньшей дисперсии.
- число вариант для меньшей дисперсии.


