
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор непроизводных элементовСодержание книги
Поиск на нашем сайте Первый этап построения синтаксической модели образов состоит в определении множества непроизводных элементов, при помощи которых можно эти образы описать.
Пример. Пусть необходимо отличать прямоугольники (разного размера) от не прямоугольников. Тогда выбирают следующие непроизводные элементы: a ′ – горизонтальный отрезок; b ′ – вертикальный отрезок; c ′ – горизонтальный отрезок; d ′ – вертикальный отрезок.
Множество всех прямоугольников (разного размера) можно представить одним предложением или цепочкой a ′ b ′ c ′ d ′.
Если задача состоит в различении прямоугольников разного размера, то это описание не годится. В этом случае в качестве непроизводных элементов нужно выбрать отрезки единичной длины:
Тогда множество прямоугольников разного размера можно описать при помощи языка:
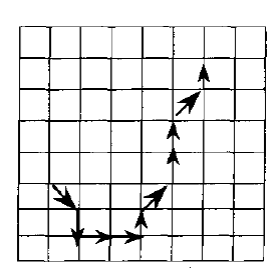
Выделение непроизводных элементов на границах Множество непроизводных элементов, которые обычно используют для описания границ, получают по схеме цепного кодирования, предложенной Фрименом. На двумерное изображение накладывают прямоугольную сетку, и узлы сетки, которые наиболее близки к точкам изображения, соединяют отрезками прямых. Каждому такому отрезку в соответствии с наклоном присваивают восьмеричное число. Таким образом, изображение представляется цепью (последовательностью) или цепями восьмеричных чисел. На рисунке показано множество начальных элементов и кодовая цепочка, описывающая кривую. Эта схема обладает рядом полезных свойств. Например, поворот изображения на угол, кратный 45°, сводится к прибавлению восьмеричного числа (сложение по модулю 8) к каждому числу цепочки. Конечно, при этом изображение может исказиться. Только поворот на угол, кратный 90°, никогда не приводит к искажениям изображения. Изменяя зернистость сетки, накладываемой на изображение, можно получить любое желаемое разрешение. Этот метод не ограничен изображения-ми с односвязными замкнутыми границами. Его можно применять для описания произвольных двумерных фигур, составленных из прямых и кривых линий и отрезков.
Цепной код Фримена. Непроизводные элементы и кодовая цепочка кривой 7600212212
Лекция 5 Кластерный анализ Кластерный анализ (самообучение, обучение без учителя, таксономия) применяется при автоматическом формировании перечня образов по обучающей выборке. Все объекты этой выборки предъявляются системе без указания, какому образу они принадлежат. Подобного рода задачи решает, например, человек в процессе естественно-научного познания окружающего мира (классификации растений, животных). Этот опыт целесообразно использовать при создании соответствующих алгоритмов. В основе кластерного анализа лежит гипотеза компактности. Предполагается, что обучающая выборка в признаковом пространстве состоит из набора сгустков. Задача системы – выявить и формализовано описать эти сгустки. Геометрическая интерпретация гипотезы компактности состоит в следующем. Объекты, относящиеся к одному таксону, расположены близко друг к другу по сравнению с объектами, относящимися к разным таксонам. "Близость" можно понимать шире, чем при геометрической интерпретации. Например, закономерность, описывающая взаимосвязь объектов одного таксона, отличается от таковой в других таксонах, как это имеет место в лингвистических методах. Мы ограничимся рассмотрением геометрической интерпретации. Остановимся на алгоритме FOREL (рис. 1).
Рис. 1. Иллюстрация алгоритма FOREL:
Строится гиперсфера радиуса В следующем цикле используются гиперсферы радиуса
Примером использования человеческих критериев при решении задач таксономии служит алгоритм KRAB. Эти критерии отработаны на двухмерном признаковом пространстве в ходе таксономии, осуществляемой человеком, и применены в алгоритме, функционирующем с объектами произвольной размерности. Факторы, выявленные при "человеческой" таксономии, можно сформулировать следующим образом: – внутри таксонов объекты должны быть как можно ближе друг к другу (обобщённый показатель – таксоны должны как можно дальше отстоять друг от друга (обобщённый показатель – в таксонах количество объектов должно быть по возможности одинаковым, то есть их различие в разных таксонах нужно минимизировать (обобщённый показатель – внутри таксонов не должно быть больших скачков плотности точек, то есть количества точек на единицу объёма (обобщённый показатель Если удастся удачно подобрать способы измерения Все точки обучающей выборки объединяются в граф, в котором они являются вершинами. Этот граф должен иметь минимальную суммарную длину рёбер, соединяющих все вершины, и не содержать петель (рис. 15). Такой граф называют КНП-графом (КНП – кратчайший незамкнутый путь).
Мера близости объектов в одном таксоне – это средняя длина ребра
где
Усреднённая по всем таксонам мера близости точек Средняя длина рёбер, соединяющих таксоны, Мера локальной неоднородности определяется следующим образом. Если длина
где Определим величину
Можно показать, что при фиксированном Теперь можно сформировать интегрированный критерий качества таксономии
Чем больше
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |







 , где
, где  соответствует гиперсфере, охватывающей все объекты (точки) обучающей выборки. При этом число таксонов
соответствует гиперсфере, охватывающей все объекты (точки) обучающей выборки. При этом число таксонов  будет равно единице. Затем строится гиперсфера радиуса
будет равно единице. Затем строится гиперсфера радиуса  с центром в произвольной точке выборки. По множеству точек, попавших внутрь гиперсферы (формального элемента), определяется среднее значение координат (эталон) и в него перемещается центр гиперсферы. Если это перемещение существенное, то заметно изменится множество точек, попавших внутрь гиперсферы, а следовательно, и их среднее значение координат. Вновь перемещаем центр гиперсферы в это новое среднее значение и т.д. до тех пор, пока гиперсфера не остановится либо зациклится. Тогда все точки, попавшие внутрь этой гиперсферы, исключаются из рассмотрения и процесс повторяется на оставшихся точках. Это продолжается до тех пор, пока не будут исчерпаны все точки. Результат таксономии: набор гиперсфер (формальных элементов) радиуса
с центром в произвольной точке выборки. По множеству точек, попавших внутрь гиперсферы (формального элемента), определяется среднее значение координат (эталон) и в него перемещается центр гиперсферы. Если это перемещение существенное, то заметно изменится множество точек, попавших внутрь гиперсферы, а следовательно, и их среднее значение координат. Вновь перемещаем центр гиперсферы в это новое среднее значение и т.д. до тех пор, пока гиперсфера не остановится либо зациклится. Тогда все точки, попавшие внутрь этой гиперсферы, исключаются из рассмотрения и процесс повторяется на оставшихся точках. Это продолжается до тех пор, пока не будут исчерпаны все точки. Результат таксономии: набор гиперсфер (формальных элементов) радиуса  с центрами, определёнными в результате вышеописанной процедуры. Назовём это циклом с формальными элементами радиуса
с центрами, определёнными в результате вышеописанной процедуры. Назовём это циклом с формальными элементами радиуса  . Здесь появляется параметр
. Здесь появляется параметр  , определяемый исследователем чаще всего подбором в поисках компромисса: увеличение
, определяемый исследователем чаще всего подбором в поисках компромисса: увеличение  несколько циклов с радиусами формальных элементов
несколько циклов с радиусами формальных элементов  будут завершаться при одинаковом числе
будут завершаться при одинаковом числе 
 );
); );
); );
); ).
). и
и  то можно добиться хорошего совпадения "человеческой" и автоматической таксономии. В алгоритме KRAB используется следующий подход.
то можно добиться хорошего совпадения "человеческой" и автоматической таксономии. В алгоритме KRAB используется следующий подход.
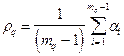 ,
, – число объектов в таксоне
– число объектов в таксоне  ,
, – длина
– длина  -го ребра.
-го ребра. .
. .
. -го ребра
-го ребра  , то чем меньше
, то чем меньше  , тем больше отличие в длинах рёбер, тем больше оснований считать, что по ребру с длиной
, тем больше отличие в длинах рёбер, тем больше оснований считать, что по ребру с длиной 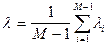 ,
, – общее число точек в обучающей выборке.
– общее число точек в обучающей выборке. .
.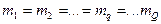 .
. .
. , тем это качество выше. Таким образом, осуществляя таксономию, нужно стремиться к максимизации
, тем это качество выше. Таким образом, осуществляя таксономию, нужно стремиться к максимизации  рёбер, таких, чтобы критерий
рёбер, таких, чтобы критерий 



