
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка информативности признаковСодержание книги
Поиск на нашем сайте Оценка информативности признаков необходима для их отбора при решении задач распознавания. Сама процедура отбора практически не зависит от способа измерения информативности. Важно лишь, чтобы этот способ был одинаков для всех признаков (групп признаков), входящих в исходное их множество и участвующих в процедуре отбора. Поскольку процедуры отбора были рассмотрены в разделе, посвящённом детерминистским методам распознавания, здесь мы на них останавливаться не будем, а обсудим только статистические методы оценки информативности. При решении задач распознавания решающим критерием является риск потерь и как частный случай – вероятность ошибок распознавания. Для использования этого критерия необходимо для каждого признака (группы признаков) провести обучение и контроль, что является достаточно громоздким процессом, особенно при больших объёмах выборок. Именно это и характерно для статистических методов. Хорошо, если обучение состоит в построении распределений значений признаков для каждого образа Если имеются обучающая и контрольная выборки, то первая из них используется для построения Можно пойти другим путём, а именно: всю выборку использовать для обучения (построения В связи с этим представляют интерес другие меры информативности признаков, вычисляемые с меньшими затратами вычислительных ресурсов, чем оценка вероятности ошибок распознавания. Такие меры могут быть не связаны взаимооднозначно с вероятностями ошибок, но для выбора наиболее информативной подсистемы признаков это не столь существенно, так как в данном случае важно не абсолютное значение риска потерь, а сравнительная ценность различных признаков (групп признаков). Смысл критериев классификационной информативности, как и при детерминистском подходе, состоит в количественной мере "разнесённости" распределений значений признаков различных образов. В частности, в математической статистике используются оценки верхней ошибки классификации Чернова (для двух классов), связанные с ней расстояния Бхатачария, Махаланобиса. Для иллюстрации приведём выражение расстояния Махаланобиса для двух нормальных распределений, отличающихся только векторами средних
где
-1 – обращение матрицы. В одномерном случае Несколько подробнее рассмотрим информационную меру Кульбака применительно к непрерывной шкале значений признаков. Определим следующим образом среднюю информацию в пространстве
При этом предполагается, что нет областей, где Аналогично Назовём расхождением величину
Чем расхождение больше, тем выше классификационная информативность признаков. Очевидно, что при Легко убедиться, что если признаки (признаковые пространства) В качестве примера вычислим расхождение двух нормальных одномерных распределений с одинаковыми дисперсиями и различными средними:
Оказывается, что в этом конкретном случае расхождение равно расстоянию Махаланобиса Промежуточные выкладки предлагается сделать самостоятельно.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 913; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . Тогда, если нам удалось построить
. Тогда, если нам удалось построить  в исходном признаковом пространстве, распределение по какому-либо признаку (группе признаков) получается как проекция
в исходном признаковом пространстве, распределение по какому-либо признаку (группе признаков) получается как проекция  и
и  :
:
 – матрица ковариаций,
– матрица ковариаций, – транспонирование матрицы,
– транспонирование матрицы, откуда видно, что
откуда видно, что  тем больше, чем удалённее друг от друга
тем больше, чем удалённее друг от друга  и
и  и компактнее распределения (меньше
и компактнее распределения (меньше  ).
). для различения в пользу
для различения в пользу  против
против  :
:
 а
а  , и наоборот.
, и наоборот.


 В других случаях
В других случаях  Действительно, если
Действительно, если  , где в области
, где в области  справедливо
справедливо  , а в
, а в  –
–  , то
, то  причём
причём 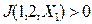 и
и  .
. независимы, то
независимы, то 






