
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление рациональной функции в виде суммы простейших дробей.Содержание книги
Поиск на нашем сайте
Теорема Правильную рациональную функцию одной переменной x можно единственным образом представить в виде суммы элементарных дробей
где A, M, N, a, p, q — действительные числа и k — натуральные числа. В этой сумме каждому действительному нулю a кратности k знаменателя Qn (x) соответствуют k слагаемых
Каждой паре комплексно сопряженных нулей кратности k знаменателя Qn (x) (являющихся нулями квадратного трехчлена x 2 + 2 px + q) соответствуют k слагаемых
Представление правильной рациональной функции в виде суммы элементарных дробей называется разложением на элементарные дроби. Коэффициенты элементарных дробей, фигурирующих в разложении, однозначно определяются условием тождественности правильной рациональной функции и ее разложения. 11. Матрицы. Операции над матрицами. Свойства сложения и умножения матриц, умножения на действительное число, транспонирования. Матрица Матрицей размера m на n (записывается так Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами:
Операции над матрицами 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B, т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц 6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Свойства сложения матриц
A + (– A) = A – A = 0, где 0 – матрица, составленная из нулевых элементов.
Свойства, связанные с умножением матриц.
12. Обратная матрица. Алгоритм нахождения обратной матрицы. Свойства обратных матриц.
Обратная Матрица Рассмотрим квадратную матрицу Обозначим Δ =det A. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0. Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица матрице А, обозначается через А-1, так что В = А-1 и вычисляется по формуле где А i j - алгебраические дополнения элементов a i j матрицы A.. Вычисление A-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицы можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.106.38 (0.009 с.) |

 )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
)называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца. - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом
- элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом






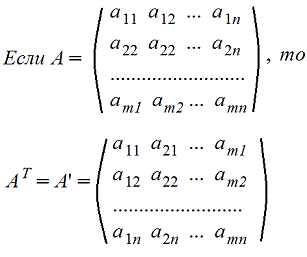
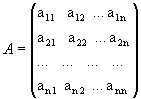 .
. , (1)
, (1)


