Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретико-множественное определениеСодержание книги
Поиск на нашем сайте
В теоретической математике функцию Это и позволяет говорить о том, что элементу Таким образом, функция — это упорядоченная тройка (или кортеж) объектов · множество · множество · множество упорядоченных пар Предел функции в точке 1. Функция одной переменной. Определение предела функции в точке по Коши. Число b называется пределом функции у = f (x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что | x – a | < d, выполняется неравенство Определение предела функции в точке по Гейне. Число b называется пределом функции у = f (x) при х, стремящемся к а (или в точке а), если для любой последовательности { x n}, сходящейся к а (стремящейся к а, имеющей пределом число а), причем ни при каком значении n х n ≠ а, последовательность { y n = f (x n)} сходится к b. Данные определения предполагают, что функция у = f (x) определена в некоторой окрестноститочки а, кроме, быть может, самой точки а. Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму. Указанный предел обозначается так:
34. Односторонние пределы. Свойства пределов функции. Односторонние пределы Односторонний предел по Коши · Число
· Число
Свойства Пределов функции · Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра. · Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой 35. Первый и второй замечательный пределы. Сравнение функций. 1) 2) Сравнение Функций а) Сравнение бесконечно малых функций Для определения бесконечно малых и бесконечно больших функций воспользуемся, так называемым сравнением функций. Пусть у нас есть две функции p(x) и q(x), которые стремятся к А при аргументе x стремящемся к А. И будем рассматривать предел их отношения при аргументе x, стремящемся к некоторому числу A. Тогда возможны следующие варианты: 1) 2) 3) Если данный предел: 4) Устали от учебы? База затока приезжай в любое время года и наслаждайся незаюываемым по красоте морем. b) Сравнение бесконечно больших функций Также как и в предыдущем пункте будем рассматривать предел отношения двух функций. Только теперь у нас функции стремятся к бесконечности при аргументе x, стремящемся к А. Возможны следующие варианты: 1) 2) 3) 4) Если данный предел: 36. Бесконечно малые и бесконечно большие функции, их свойства. Понятие неопределенности. Бесконечно малая функция Рассмотрим функцию ПРИМЕР 1. Бесконечно малые функции Сравнение бесконечно малых функций. Пусть ПРИМЕР 2. Сравнение бесконечно малых функций Эквивалентные бесконечно малые функции. Если Бесконечно Большая функция БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:
37. Непрерывность функции в точке. Свойства непрерывных функций.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.008 с.) |

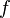 удобно определить как бинарное отношение (то есть множество упорядоченных пар
удобно определить как бинарное отношение (то есть множество упорядоченных пар 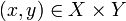 ), которое удовлетворяет следующему условию: для любого[3]
), которое удовлетворяет следующему условию: для любого[3] 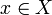 существует единственный элемент
существует единственный элемент 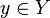 такой, что
такой, что 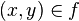 .
. , где
, где называется о́бластью определе́ния;
называется о́бластью определе́ния;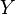 называется о́бластью значе́ний;
называется о́бластью значе́ний; или, что то же самое, график функции.
или, что то же самое, график функции.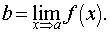
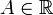 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции 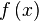 в точке
в точке  , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число  такое, что для всех точек
такое, что для всех точек 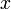 из интервала
из интервала 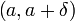 справедливо неравенство
справедливо неравенство 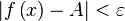 .
.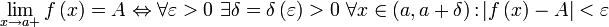
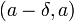 справедливо неравенство
справедливо неравенство 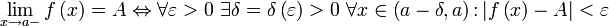
 ; (Первый замечательный предел)
; (Первый замечательный предел)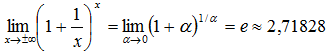 (Второй замечательный предел)
(Второй замечательный предел)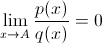 , т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)).
, т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)).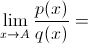 , т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)).
, т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)). не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.
не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.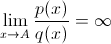 , т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)).
, т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)).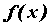 , определенную в некоторой окрестности
, определенную в некоторой окрестности 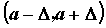 точки
точки 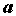 ,
, 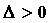 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , стремящемся к
, стремящемся к 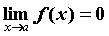 . Если
. Если 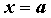 , то для любого положительного числа
, то для любого положительного числа 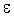 , как бы мало оно ни было, существует такое положительное число
, как бы мало оно ни было, существует такое положительное число 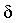 , что для всех
, что для всех 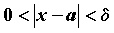 , справедливо неравенство
, справедливо неравенство 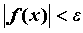 . Неравенства
. Неравенства  ,
,  , означают, что для любого
, означают, что для любого 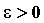 существует такое
существует такое 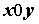 . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию
. Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию 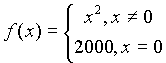 . При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.
. При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.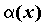 и
и  — две функции, бесконечно малые в точке
— две функции, бесконечно малые в точке 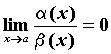 , то говорят, что
, то говорят, что 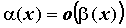 . Если же
. Если же  , то
, то 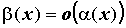 . Бесконечно малые функции
. Бесконечно малые функции 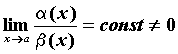 , обозначают
, обозначают 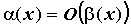 . И, наконец, если
. И, наконец, если 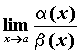 не существует, то бесконечно малые функции
не существует, то бесконечно малые функции 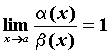 , то бесконечно малые функции
, то бесконечно малые функции  .
.