
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Предел функции. Эквивалентные функции.Содержание книги
Поиск на нашем сайте
Определение предела функции при Тема 9. Непрерывность функции. Непрерывность функции в точке. Точки разрыва функции и их классификация. Раздел V. КОМПЛЕКСНЫЕ ЧИСЛА. АЛГЕБРА МНОГОЧЛЕНОВ. Тема 10. Комплексные числа. Комплексные числа, их изображение на плоскости. Действия над комплексными числами (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня). Многочлены и алгебраические уравнения. Разложение многочленов на линейные и квадратичные множители. Литература: [6]. С.39-48, 68-92. 2.3. Виды самостоятельной работы студентов. Самостоятельная работа студентов предполагает изучение теоретического материала и выполнение одной контрольной работы. 3. Рекомендуемая литература. Основная литература: 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М: Наука, 1998. 2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов. Учеб. пособие для вузов. -М.: ЮНИТИ-ДАНА, 1997. 3. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс._3-е изд. –М.:Айрис-пресс, 2005.-608с. 4. Шипачев В.С. Высшая математика. Учебник для вузов. -М. Высшая школа, 2002. 5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть 1. Учеб. пособие для втузов. -М: Высшая школа, 1997. 6. Сборник задач по математике для втузов. Часть1. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П. -М: Наука, 1993.
Дополнительная литература:
7. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. -2-е изд., испр.-М.: Физико-математическая литература, 2001.-368с. 8. Сборник задач по математике для вузов. Под ред. Котляра Л.М., Углова А.Н. -Наб. Челны: Изд-во КамПИ, 2004.
4. Методические указания по изучению дисциплины. В процессе изучения данной дисциплины студенты должны сначала изучить теоретический материал и выработать навыки решения типовых задач, используя рекомендованную литературу, а затем выполнить одну контрольную работу (задания для контрольной работы приведены в разделе 5.1).
При выполнении контрольной работы необходимо придерживаться указанных ниже правил: 1. Контрольная работа должна быть выполнена студентом в отдельной ученической тетради с полями не менее 3 см для замечаний преподавателя. 2. На обложке тетради указываются: название дисциплины; номер варианта и номера решаемых задач; Ф.И.О. студента, выполнившего работу, его номер группы и номер зачетной книжки; Ф.И.О. преподавателя, проверяющего работу (образец оформления обложки приведён в Приложении 3). 3. Номер варианта соответствует номеру студента в списке группы. 4. Номера решаемых задач выбираются из каждого раздела по номеру варианта. 5. Условия задач переписываются полностью, без сокращения слов, после чего приводится их подробное решение (чертежи можно выполнять аккуратно от руки). В конце решения приводится ответ. 6. В работу должны быть включены все задачи, указанные в задании, строго по порядку номеров. Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются. 7. Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку. 8. Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления. 9. Работа может быть выполнена заново в случае выявления серьёзных замечаний и ошибок. 10. В конце тетради рекомендуется оставлять несколько чистых страниц для дополнений и исправлений. После проверки контрольная работа предъявляется к защите. На защите студент должен показать свое умение решать задачи, подобные тем, что имеются в его контрольной работе. Образец решения типового варианта контрольной работы приведён в Приложении 1. 5. Материалы для контроля знаний студентов. Итоговой формой контроля знаний является экзамен в конце семестра обучения. На экзамене студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2 и умение решать задачи, подобные тем, что имеются в его контрольной работе.
Задания для контрольной работы.
1.1 – 30. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по 1. 1
1.4.
1.7.
1.10.
1.13.
1.16.
1.19.
1.22. . 1.25.
1.28.
2.1 – 30. Найти: а) матрицу 2.1. 2.3. 2.5. 2.7. 2.9. 2.11. 2.13. 2.15. 2.17. 2.19. 2.21. 2.23. 2.25. 2.27. 2.29.
3.1 – 30. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. 3.1. 3.3. 3.5. 3.7. 3.9. 3.11.
3.13. 3.15. 3.17. 3.19. 3.21. 3.23. 3.25. 3 .27. 3.29 4.1–30. Найти общее решение для каждой из данных систем методом Гаусса:
4.1 а) 4.2 а) 4.3 а) 4.4 а) 4.5 а) 4.6 а) 4.7 а) 4.8 а) 4.9 а) 4.10 а) 4.13 а) 4.14 а) 4.15 а) 4.16 а) 4.17 а) 4.18 а) 4.19 а) 4.21 а) 4.22 а) 4.23 а) 4.24 а) 4.26 а) 4.27 а) 4.28 а) 4.29 а) 4.30 а) 5.1 – 30. Даны векторы а) вычислить скалярное произведение векторов
5.1 5.2. 5.3. 5.4. 5.5. 5.6. 5.7. 5.8. 5.9. 5.10. 5.11. 5.12. 5.13. 5.14. 5.15. 5.16. 5.17. 5.18. 5.19. 5.20. 5.21. 5.22. 5.23. 5.24. 5.25. 5.26. 5.27. 5.28. 5.29. 5.30. 6.1-30. Даны вершины треугольника а) длину стороны в) уравнение медианы г) уравнение высоты д) длину 6.1. 6.3. 6.5. 6.7. 6.9. 6.11. 6.13. 6.15. 6.17. 6.19. 6.21. 6.23. 6.25. 6.27. 6.29. 7.1 – 30. Даны вершины пирамиды а) длины ребер в) площадь грани д) уравнение плоскости грани е) длину 7.1. 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10. 7.11. 7.12. 7.13. 7.14. 7.15. 7.16. 7.17. 7.18. 7.19. 7.20. 7.21. 7.22. 7.23. 7.24. 7.25. 7.26. 7.27. 7.28. 7.29. 7.30. 8.1–30. Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её. 8.1. 8.3 8.5. 8.7. 8.9. 8.11 8.13. 8.15. 8.17. 8.27. 8.29. 9.1 – 30. Для указанной функции найтиобласть определения функции; 9.1. а) 9.2. а) 9.3. а) 9.4. а) 9.5. а) 9.6. а) 9.7. а) 9.8. а) 9.9. а) 9.10. а) 9.11 а) 9.12 а) |

 . Неопределённые выражения. Вычисление пределов рациональных и иррациональных выражений. Вычисление пределов с помощью первого и второго замечательного пределов. Вычисление пределов с помощью принципа замены эквивалентных бм функций. Односторонние пределы, их вычисление.
. Неопределённые выражения. Вычисление пределов рациональных и иррациональных выражений. Вычисление пределов с помощью первого и второго замечательного пределов. Вычисление пределов с помощью принципа замены эквивалентных бм функций. Односторонние пределы, их вычисление. строке;
строке;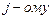 столбцу.
столбцу.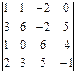 1.2.
1.2.  1.3.
1.3. 

 .
. 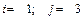 .
. 1.5.
1.5.  1.6.
1.6. 
 .
. 
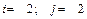
 1.8.
1.8.  1.9.
1.9. 
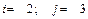 .
.  .
. 
 1.11.
1.11. 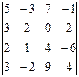 1.12.
1.12. 
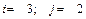 .
. 
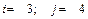
 1.14.
1.14.  1.15.
1.15. 
 .
. 

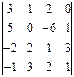 1.17.
1.17.  1.18.
1.18. 


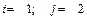
 1.20.
1.20. 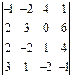 1.21.
1.21. 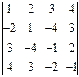
 .
.  .
. 
 1.23.
1.23.  1.24.
1.24. 
 .
. 

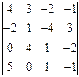 1.26.
1.26.  1.27.
1.27. 



 1.29.
1.29. 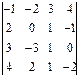 1.30.
1.30. 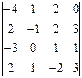


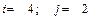
 , если
, если  ;
;
 ,
, 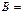
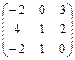 2.2.
2.2. 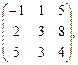
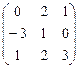
 ,
,  2.4.
2.4.  ,
, 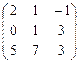
 ,
,  2.6.
2.6.  ,
, 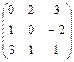
 ,
,  2.8.
2.8.  ,
, 
 ,
, 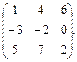 2.10.
2.10. 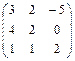 ,
, 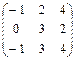
 ,
,  2.12.
2.12.  ,
, 
 ,
, 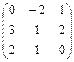 2.14.
2.14. 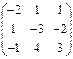 ,
, 
 ,
,  2.16.
2.16.  ,
, 
 ,
,  2.18.
2.18.  ,
, 
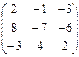 ,
,  2.20.
2.20.  ,
, 
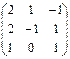 ,
,  2.22.
2.22.  ,
, 
 ,
, 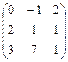 2.24.
2.24. 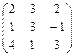 ,
, 
 ,
, 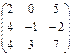 2.26.
2.26.  ,
, 
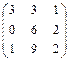
 ,
,  2.28.
2.28.  ,
, 
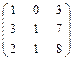 ,
,  2.30.
2.30.  ,
, 
 3.2.
3.2. 
 3.4.
3.4. 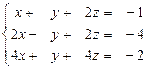
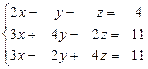 3.6.
3.6. 
 3.8.
3.8. 
 3.10.
3.10. 
 3.12.
3.12. 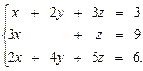
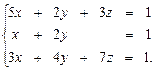 3.14.
3.14. 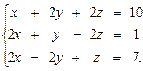
 3. 16.
3. 16. 
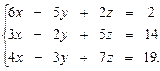 3.18.
3.18. 
 3.20.
3.20. 
 3.22.
3.22. 
 3.24.
3.24. 
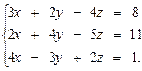 3.26.
3.26. 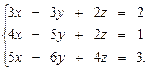
 3.28.
3.28. 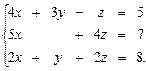
 3.30
3.30 
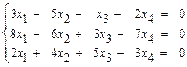 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 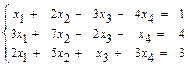
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
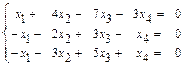 б)
б)  4.11 а)
4.11 а)  б)
б)  4.12 а)
4.12 а)  б)
б) 
 б)
б) 
 б)
б) 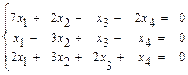 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б)  4.20 а)
4.20 а)  б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 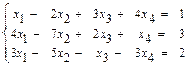
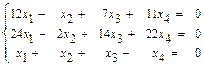 б)
б)  4.25 а)
4.25 а)  б)
б) 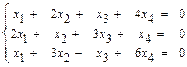 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 . Требуется:
. Требуется: , если
, если  ,
,  ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов  ; в) показать, что векторы
; в) показать, что векторы  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.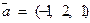 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.








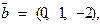
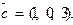


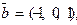

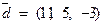
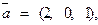

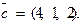




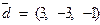




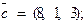









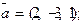 ,
, 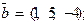 ,
, 




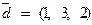







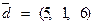
 ,
, 
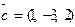 ;
; 



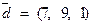
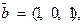


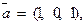













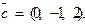


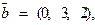

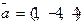
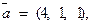












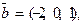






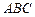 . Требуется найти:
. Требуется найти: ; б) уравнение стороны
; б) уравнение стороны  , проведённой из вершины
, проведённой из вершины  ;
;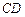 , проведённой из вершины
, проведённой из вершины  высоты
высоты  треугольника
треугольника 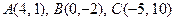 . 6.2.
. 6.2. 
 6.4.
6.4. 
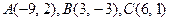 6.6.
6.6. 
 6.8.
6.8. 
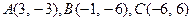 6.10.
6.10. 
 6.12.
6.12. 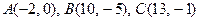
 6.14.
6.14. 
 6.16.
6.16. 
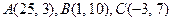 6.18.
6.18. 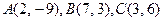
 6.20.
6.20. 
 6.22.
6.22. 
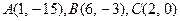 6.24.
6.24. 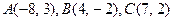
 6.26.
6.26. 
 6.28.
6.28. 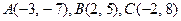
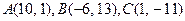 6.30.
6.30. 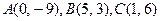
 . Требуется найти:
. Требуется найти: ; б) угол между ребрами
; б) угол между ребрами  ;
; пирамиды
пирамиды 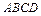 .
.

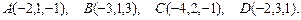
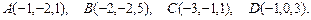



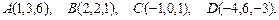





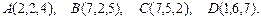






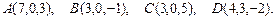


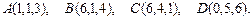




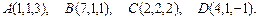

 8.2.
8.2. 
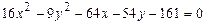 8.4
8.4 
 8.6.
8.6. 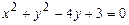
 8.8.
8.8. 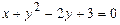
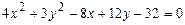 8.10.
8.10. 
 8.12.
8.12. 
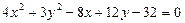 8.14.
8.14. 
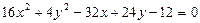 8.16.
8.16. 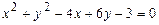
 8.18.
8.18. 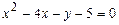 8.19.
8.19. 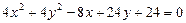 8.20.
8.20.  8.21.
8.21.  8.22.
8.22.  8.23.
8.23.  8.24.
8.24.  8.25.
8.25.  8.26.
8.26. 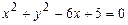
 8.28.
8.28. 
 8.30.
8.30. 
 требуется
требуется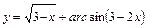 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 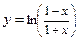
 б)
б) 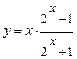
 б)
б) 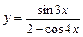
 б)
б) 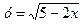
 б)
б) 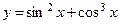
 б)
б) 
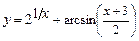 б)
б) 
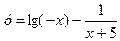 б)
б) 



