Тема 3. Системы линейных уравнений.

Системы линейных уравнений (СЛУ). Основные понятия и определения. Матричная запись СЛУ. Теорема Кронеккера-Капелли. Формулы Крамера. Решение СЛУ методом обратной матрицы. Решение СЛУ методом Гаусса. Однородные системы линейных уравнений, свойства их решений.

Литература: [1] –C.136-142; 154-159; 165-174; [2] – C.38-53;

[3] – C.29-38; [4] – C.268-276.

 

 

Раздел II. ВЕКТОРНАЯ АЛГЕБРА

Тема 4. Векторная алгебра.

Геометрические векторы на прямой, плоскости и в пространстве, линейные операции над ними. Линейная комбинация векторов. Линейно зависимая и линейно независимая система векторов. Базис плоскости, пространства. Системы координат на плоскости и в пространстве, координаты вектора. Линейные операции над векторами в координатной форме. Проекция вектора. Прямоугольная декартова система координат. Радиус-вектор. Длина и направляющие косинусы вектора. Расстояние между точками. Деление отрезка в данном отношении. Скалярное, векторное, смешанное произведения векторов, их свойства, выражение в координатной форме, приложения для решения геометрических задач. Условия перпендикулярности, параллельности и компланарности векторов.

Литература: [1] –C.5-37; [2] – C.63-68; [3] – C.39-57; [4] – C.222-241.

Раздел III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Тема 5. Прямые линии и плоскости.

Прямая на плоскости. Различные виды уравнений прямой на плоскости. Расстояние от точки до прямой. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Плоскость. Различные виды уравнений плоскости. Взаимное расположение 2-ух плоскостей. Расстояние от точки до плоскости. Прямая в пространстве. Различные виды уравнений прямой в пространстве. Взаимное расположение 2-ух прямых в пространстве. Взаимное расположение прямой и плоскости

Литература: [1] –C.45-71; [2] – C.95-104; 119-121;

[3] – C.68-74; 92-104; [4] – C.34-52; 244-252.

 

Тема 6. Кривые и поверхности второго порядка

Кривые 2-ого порядка на плоскости: окружность, эллипс, гипербола, парабола, их определения, канонические уравнения, форма. Приведение общего уравнения кривой 2-ого порядка к каноническому виду и построение. Поверхности 2-ого порядка, их канонические уравнения и форма. Метод сечения при исследовании формы поверхности.

 

Литература: [1] –C.72-110; [2] – C.104-115; [3] – C.74-89; 104-115;

[4] – C.52-69; 252-259.

Раздел IV. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

Тема 7. Функциональная зависимость.

Понятие функции. Способы задания функции. График функции. Основные элементы поведения функции. Основные элементарные функции, их свойства и графики. Обратная и сложная функции. Элементарные функции, их классификация. Построение графиков функций.

Литература: [1] –C.15-24; 46-58; 88-91; [2] –C123-140.; [3] –C. 120-27; [5] –C.10-19; 69-73; 100-102.

Тема 8. Предел функции. Сравнение бм функций. Эквивалентные бм функции.

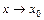Определения предела функции при , при 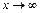. Геометрический смысл предела. Односторонние пределы. Бесконечно большие и малые функции, их свойства. Основные теоремы о пределах функций. Предельный переход в неравенствах. Первый и второй замечательные пределы. Эквивалентные бесконечно малые функции, их свойства и применение при вычислении пределов.

Литература: [1] –C.58-73; [2] –C.143-159; [3] – C.132-53; 59-60; [5] – C.73-87.