
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел V. Комплексные числа. Алгебра многочленов.Содержание книги
Поиск на нашем сайте
56. Комплексное число, его изображение на плоскости. Комплексно-сопряжённое число. Модуль и аргумент комплексного числа. Различные формы записи комплексного числа (алгебраическая, тригонометрическая, показательная). Формула Эйлера. 57. Действия над комплексными числами (сложение, вычитание, умножение, деление) в алгебраической, тригонометрической и показательной формах. 58. Возведение комплексного числа в степень. Формула Муавра. Извлечение корня из комплексного числа. 59. Понятие многочлена, алгебраического уравнения. Основная теорема алгебры и теорема Безу. Разложение многочлена на множители. Нахождение корней квадратного уравнения. Приложения. 6.1. Образец решения контрольных задач типового варианта. 1.1 – 30. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по Решение. а) вычисляем определитель разложением по элементам первой строки:
Тогда б) вычисляем определитель непосредственным разложением по элементам второго столбца:
Тогда Ответ: 2.1-30. а) Найти матрицу
Решение: 1) Транспонируем матрицу 2) Вычисляем произведение матриц
3) Находим матрицу
4) Находим матрицу
Ответ: 3.1 – 30. Дана система уравнений: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. Решение. А) Метод Крамера. 1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:
2а) Так как 3а) Вычисляем определители
4а) Находим решение: 5а) Выполняем проверку: Ответ: Б) Метод обратной матрицы. 1б) Записываем систему уравнений в матричном виде:
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:
3б) Так как
4б) Находим обратную матрицу
Тогда 5б) Находим решение:
6б) Выполняем проверку: Ответ: В) Метод Гаусса. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса. В результате прямого хода матрица системы
Замечание. Если при выполнение преобразования расширенной матрицы 3в) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 4в) Выполняем проверку: Ответ:
4.1-30. Найти общее решение для каждой из данных систем методом Гаусса: а) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных 3а) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:
Тогда общее решение системы запишется в виде: 4а) Выполняем проверку:
Ответ: б) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Замечание. В результате прямого хода матрица системы Если, при выполнении преобразования расширенной матрицы Для выполнения условия
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных 3б) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: Тогда общее решение системы запишется в виде:
4б) Выполняем проверку:
Ответ: в) Решение. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса.
При выполнении преобразования расширенной матрицы Ответ: Система несовместна. 5.1– 30. Даны векторы Решение. 1a). Находимвектор
= 2а) Находимвектор
= 3а) Вычисляем скалярное произведениевекторов
б) Вычисляем векторное произведение векторов
= 1в) Покажем, что векторы
Так как 2в) Записываем разложение вектора
Коэффициенты разложения 3в) Записываем векторное уравнение относительно
Таким образом: Ответ: 6.1-30. Даны вершины треугольника а) длину стороны в) уравнение медианы г) уравнение высоты д) длину Решение. Сделаем чертёж:
а) Длинустороны
б) Уравнение стороны
в) Уравнение медианы
Тогда:
г) Уравнение высоты д) Длину
е) Площадь треугольника Ответ: а) г)
7.1 – 30. Даны вершины пирамиды а) длины ребер в) площадь грани д) уравнение плоскости грани е) длину Решение. а) Длинырёбер
б) Угол в) Площадь
г) Объём
получим д) Уравнение плоскости грани
е) Длину
Ответ: а) г) 8.1–30. Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её: а) в) Решение: а) Выделяя полные квадраты в левой части уравнения
Полученное уравнение определяет гиперболу с центром в точке
Ответ: Гипербола с центром в точке
Рис.1
б) Выделяя полные квадраты в левой части уравнения
Полученное уравнение определяет эллипс с центром в точке Ответ: Эллипс с центром в точке в). Выделяя полные квадраты в левой части ур
|
||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.152.153 (0.014 с.) |



 строке;
строке;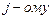 столбцу;
столбцу;
 .
.





 =
=  =
= 

 .
.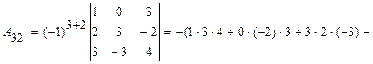



 .
. .
. , если:
, если: ,
,  .
. :
:  .
.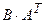 :
:

 .
. :
:
 .
. :
: 

 .
. .
. . Требуется:
. Требуется:
 .
. , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 
 :
: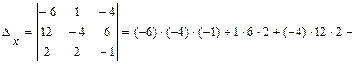
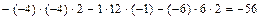 ,
,
 ,
,
 .
. .
.
 .
. .
. или
или 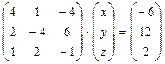

 , то матрица системы
, то матрица системы  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой: или
или 
 (методом присоединённой матрицы):
(методом присоединённой матрицы): .
.








 .
.
 .
. .
. .
. .
. должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами  . Система уравнений, матрица которой
. Система уравнений, матрица которой  , имеет единственное решение, а система уравнений, матрица которой
, имеет единственное решение, а система уравнений, матрица которой  , имеет бесконечно много решений.
, имеет бесконечно много решений.

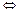


 . В результате элементарных преобразований матрица
. В результате элементарных преобразований матрица  . Система уравнений, матрица которой
. Система уравнений, матрица которой  в преобразованной матрице
в преобразованной матрице  появляется строка
появляется строка  , где
, где  , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений. и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:
и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:  .
. .
. .
.







 .
. и
и  :
:  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  и
и  .
. . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:  .
. .
.
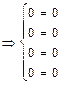 .
. .
. .
.







 .
. . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  .
.



 .
. .
.



 .
. , соответствующая уравнению
, соответствующая уравнению  , которому не удовлетворяет ни один набор значений неизвестных
, которому не удовлетворяет ни один набор значений неизвестных  , что говорит о несовместности исходной системы уравнений.
, что говорит о несовместности исходной системы уравнений. :
:  ;
;  ;
;  ;
;  . Требуется: а) вычислить скалярное произведение векторов
. Требуется: а) вычислить скалярное произведение векторов  , если
, если  ,
,  ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов  ; в) показать, что векторы
; в) показать, что векторы  образуют базис
образуют базис  и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.

 .
.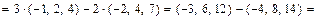

 .
.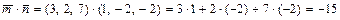 .
.

 образуют базис
образуют базис  .
. , то векторы
, то векторы  единственным образом можно разложить по векторам этого базиса.
единственным образом можно разложить по векторам этого базиса. :
: или
или  .
. ,
,  ,
,  называют координатами вектора
называют координатами вектора 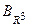 и записывают:
и записывают:  .
. , и находим единственное решение системы, например, по формулам Крамера:
, и находим единственное решение системы, например, по формулам Крамера: , где
, где ,
,  ,
,  ,
,  .
. ,
,  ,
,  . Следовательно, разложение имеет вид:
. Следовательно, разложение имеет вид:  или кратко:
или кратко:  .
. .
.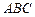 :
:  ,
,  ,
, 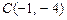 Требуется найти:
Требуется найти: ; б) уравнение стороны
; б) уравнение стороны  , проведённой из вершины
, проведённой из вершины  , проведённой из вершины
, проведённой из вершины  ;
; высоты
высоты  треугольника
треугольника  . Сделать чертёж.
. Сделать чертёж.
 :
: ,
, .
. и
и  , и записываем его в виде общего уравнения прямой:
, и записываем его в виде общего уравнения прямой:



 .
. , и записываем его в виде общего уравнения прямой. Неизвестные координаты точки
, и записываем его в виде общего уравнения прямой. Неизвестные координаты точки  находим как координаты точки, делящей сторону
находим как координаты точки, делящей сторону  пополам:
пополам: ;
;  .
.




 .
. перпендикулярно вектору
перпендикулярно вектору 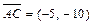 , который принимаем за нормальный вектор прямой
, который принимаем за нормальный вектор прямой 


 высоты
высоты  :
: .
. . Откуда
. Откуда  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
.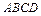 . Требуется найти:
. Требуется найти: и
и 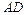 ; б) угол между ребрами
; б) угол между ребрами  ; г) объем пирамиды
; г) объем пирамиды  и
и  :
: ;
; ;
; ;
; .
. между рёбрами
между рёбрами  . Учитывая, что:
. Учитывая, что:  ,
,  ,
,  получим
получим  . Откуда
. Откуда 
 грани
грани  . Учитывая, что:
. Учитывая, что: 
 ,
, 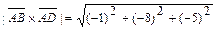 , получим
, получим  .
. пирамиды
пирамиды  . Учитывая, что:
. Учитывая, что: ,
, ,
, .
. ,
,  и
и  , и записываем его в виде общего уравнения плоскости:
, и записываем его в виде общего уравнения плоскости:




 до плоскости
до плоскости  .
. ,
,  ; б)
; б)  ; в)
; в) 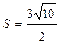 ;
; ; д)
; д) 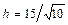 .
. ; б)
; б)  ;
; .
.



 .
.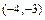 и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат
и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат  : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы  и
и  параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
 , преобразуем его следующим образом:
, преобразуем его следующим образом: 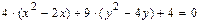



 .
. и осями симметрии параллельными осям координат. Для построения эллипса в системе координат
и осями симметрии параллельными осям координат. Для построения эллипса в системе координат  и
и  параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).


