
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые сведения о последовательностяхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Им. Д. И. Менделеева
Ряды (Теория и практика)
СОДЕРЖАНИЕ Лекция 1. Числовой ряд. Основные понятия, свойства сходящихся рядов. Знакоположительные ряды. Интегральный признак Коши…………….. 4 1.1. Некоторые сведения о последовательностях…………………………. 4 1.2. Числовой ряд. Основные понятия теории числовых рядов: сходмость, расходимость, сумма ряда. Примеры……………………………………… 5 1.3. Основные свойтсва сходящихся рядов, необходимый признак сходимости…………………………………………………………………… 8 1.4. Знакопостоянные ряды, ряды с положительными членами……………… 12 1.5. Интегральный признак Коши сходимости ряда с положительными членами……………………………………... ………………………………. 13 Лекция 2. Признаки сходимости рядов с положительными членами: признаки сравнения, признак Даламбера, радикальный признак Коши… 17 2.1. Ряды Дирихле и их сходимость, гармонический ряд…………….............. 17 2.2. Признаки сравнения рядов с положительными членами……………….... 18 2.3. Признак Даламбера сходимости рядов с положительными членами…… 22 2.4. Радикальный признак Коши сходимости рядов с положительными членами……………………………………………………………………… 25 Лекция 3. Знакочередующиеся ряды. Абсолютная и условная сходимость знакопеременных рядов……………………………………………………. 27 3.1. Знакочередующиеся ряды. Признак Лейбница........................................... 27 3.2. Знакопеременные ряды. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременных рядов……………. 29 3.3. Свойства абсолютно и условно сходящихся рядов……………………… 34 Лекция 4. Функциональные ряды. Степенные ряды. Формула Тейлора.. 35 4.1. Функциональные ряды: основные понятия, область сходимости………. 35 4.2. Степенные ряды: основные понятия, теорема Абеля……………………. 37 4.3. Свойтсва степенных рядов…………………………………………………. 42 4.4. Формула Тейлора…………………………………………………………… 43 Лекция 5. Ряды Тейлора и Маклорена……………………………………. 49 5.1. Ряды Тейлора и Маклорена. Условия сходимости рядов Тейлора к исходной функции…………………………………………………………………. 49 5.2. Разложение основных элементарных функций в степенные ряды…….. 53 Задания по теме «Ряды»……………………………………………………. 61 1. Числовые ряды. Ряды с положительными членами…………………… 61 2. Знакопеременные ряды……………………………………………....... 66 3. Функциональные ряды………………………………………………… 69 4. Ответы………………………………………………………………… 72
Лекция 1. Числовой ряд. Основные понятия, свойства сходящихся рядов. Знакоположительные ряды. Интегральный признак Коши Лекция 2. Признаки сходимости рядов с положительными членами: признаки сравнения, признак Даламбера, радикальный признак Коши
Ряды Дирихле и их сходимость, гармонический ряд Определение 1. Числовой ряд вида Пример 1. Исследовать ряд Дирихле Решение. 1) В случае, если 2) В случае –Если –Если 3) В случае Вывод: ряд Дирихле Лекция 3. Знакочередующиеся ряды. Абсолютная и условная сходимость знакопеременных рядов Свойства абсолютно и условно сходящихся рядов Свойство 1. Если ряд Свойство 2. Если ряд Свойство 3. Если ряды Свойство 4 (теорема Римана). Если ряд условно сходится, то какое бы мы не взяли число А, можно переставить члены данного ряда так, чтобы его сумма оказалась в точности равной А; более того, можно так переставить члены условно сходящегося ряда, чтобы после этого он расходился.
Свойства степенных рядов Рассмотрим степенной ряд Свойство 1. Степенной ряд Свойство 2. Если отрезок
где Свойство 3. Сумма степенного ряда есть функция, имеющая внутри интервала сходимости производные любого порядка. Производные от суммы степенного ряда будут суммами рядов, полученных из данного степенного ряда почленным дифференцированием соответствующее число раз, причём радиусы сходимости таких рядов будут те же, что и у исходного ряда. Если Формула Тейлора Рассмотрим важную задачу, которая решается в теории функциональных рядов: по заданной функции найти сходящийся функциональный ряд того или иного типа, сумма которого в области сходимости равнялась бы заданной функции. Такая задача называется разложением функции в ряд, например, степенной. Пусть функция х 0: Задача: Подберём многочлен n -й степени
Коэффициенты многочлена
Для нахождения этих коэффициентов найдём производные до n -го порядка от
…
Подставим в эти соотношения
Находим выражения для
Получаем общую формулу для определения коэффициентов многочлена
Тогда многочлен примет следующий вид: по степеням Таким образом, для каждой функции Разность
Формула (5) называется формулой Тейлора для функции
Величина остаточного члена формулы Тейлора 1) Остаточный член в форме Пеано. Преобразуем остаточный член формулы Тейлора, используя некоторые понятия из теории пределов. а) Функция б) Бесконечно малая функция Рассмотрим формулу Тейлора для функции Формула Тейлора 2) Остаточный член в форме Лагранжа. Запишем остаточный член в виде
Рассмотрим частные случаи формулы Тейлора. – Если в формуле Тейлора с остаточным членом в форме Лагранжа положить – Если в формуле Тейлора положить
где остаточный член можно записать в форме Пеано:
Формула Маклорена является разложением функции Пример 5. Разложить функцию порядка по степеням Решение. Запишем формулу Тейлора для функции виде многочлена 3-го порядка с остаточным членом в форме Лагранжа
где Находим производные нужного порядка в точке
Полученные данные подставляем в формулу Тейлора Можно сказать, что функция
Задания по теме «Ряды» Выражение вида
где – Если члены ряда: · числа, то ряд называется числовым;
· числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
· тригонометрические функции, то ряд называется тригонометрическим. Основные понятия числового ряда Числовым рядом называется сумма вида
где Суммы:
составленные из первых членов ряда (1), называются частичными суммами этого ряда. Каждому ряду можно сопоставить последовательность частичных сумм Если при бесконечном возрастании номера n частичная сумма ряда
Эта запись равносильна записи
Если частичная сумма ряда (1) при неограниченном возрастании n не имеет конечного предела (стремится к Задание 1. Найти общий член числового ряда:
Ряд Дирихле Ряд Задание 3. Исследовать на сходимость по признакам сравнения:
Признак Даламбера. Если для ряда с положительными членами Признак Даламбера не даёт решения, если Задание 4. Исследовать на сходимость по признаку Даламбера:
Интегральный признак Коши. Пусть функция f(x) при x ≥1 удовлетворяет условиям: 1) непрерывна, 2) положительна, 3) монотонно убывает. Тогда числовой ряд одновременно со сходимостью или расходимостью интеграла Задание 5. Исследовать на сходимость по интегральному признаку Коши следующие ряды:
Знакопеременные ряды Функциональные ряды Степенные ряды Степенным рядом называется ряд вида:
Областью сходимости степенного ряда называется множество всех значений Число R называется радиусом сходимости степенного ряда, если при
т.е. если степенной ряд сходится при любых Если Сходимость степенного ряда при Пример 2. Найти область сходимости ряда. Решение. Найдём радиус сходимости ряда:
Следовательно, ряд сходится при При
Ответы: Задание 1. 1) 8) Задание 2. 1) да, 2) да, 3) да, 4) нет, 5) нет, 6) да, 7) да, 8) нет, 9) нет, 10) да. Задание 3. 1)сходится, 2) расходится, 3) расходится, 4) расходится, 5) сходится, 6) сходится, 7) расходится, 8) расходится, 9) сходится, 10) сходится. Задание 4. 1) расходится, 2) сходится, 3) сходится, 4) сходится, 5) сходится, 6) сходится, 7) сходится, 8) расходится, 9) сходится, 10) расходится. Задание 5. 1) расходится, 2) сходится, 3) сходится, 4) расходится, 5) сходится, 6) расходится, 7) сходится, 8) расходится, 9) расходится, 10) расходится. Задание 6. 1) абсолютно сходится, 2) условно сходится, 3) условно сходится, 4) условно сходится, 5) абсолютно сходится, 6) абсолютно сходится, 7) абсолютно сходится, 8) абсолютно сходится, 9) условно сходится, 10) условно сходится. Задание 7. 1) (-2;2], 2) Им. Д. И. Менделеева
Ряды (Теория и практика)
СОДЕРЖАНИЕ Лекция 1. Числовой ряд. Основные понятия, свойства сходящихся рядов. Знакоположительные ряды. Интегральный признак Коши…………….. 4 1.1. Некоторые сведения о последовательностях…………………………. 4 1.2. Числовой ряд. Основные понятия теории числовых рядов: сходмость, расходимость, сумма ряда. Примеры……………………………………… 5 1.3. Основные свойтсва сходящихся рядов, необходимый признак сходимости…………………………………………………………………… 8 1.4. Знакопостоянные ряды, ряды с положительными членами……………… 12 1.5. Интегральный признак Коши сходимости ряда с положительными членами……………………………………... ………………………………. 13 Лекция 2. Признаки сходимости рядов с положительными членами: признаки сравнения, признак Даламбера, радикальный признак Коши… 17 2.1. Ряды Дирихле и их сходимость, гармонический ряд…………….............. 17 2.2. Признаки сравнения рядов с положительными членами……………….... 18 2.3. Признак Даламбера сходимости рядов с положительными членами…… 22 2.4. Радикальный признак Коши сходимости рядов с положительными членами……………………………………………………………………… 25 Лекция 3. Знакочередующиеся ряды. Абсолютная и условная сходимость знакопеременных рядов……………………………………………………. 27 3.1. Знакочередующиеся ряды. Признак Лейбница........................................... 27 3.2. Знакопеременные ряды. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременных рядов……………. 29 3.3. Свойства абсолютно и условно сходящихся рядов……………………… 34 Лекция 4. Функциональные ряды. Степенные ряды. Формула Тейлора.. 35 4.1. Функциональные ряды: основные понятия, область сходимости………. 35 4.2. Степенные ряды: основные понятия, теорема Абеля……………………. 37 4.3. Свойтсва степенных рядов…………………………………………………. 42 4.4. Формула Тейлора…………………………………………………………… 43 Лекция 5. Ряды Тейлора и Маклорена……………………………………. 49 5.1. Ряды Тейлора и Маклорена. Условия сходимости рядов Тейлора к исходной функции…………………………………………………………………. 49 5.2. Разложение основных элементарных функций в степенные ряды…….. 53 Задания по теме «Ряды»……………………………………………………. 61 1. Числовые ряды. Ряды с положительными членами…………………… 61 2. Знакопеременные ряды……………………………………………....... 66 3. Функциональные ряды………………………………………………… 69 4. Ответы………………………………………………………………… 72
Лекция 1. Числовой ряд. Основные понятия, свойства сходящихся рядов. Знакоположительные ряды. Интегральный признак Коши Некоторые сведения о последовательностях Пусть каждому значению Определение 1. Последовательность Определение 2. Последовательность Определение 3. Последовательность ( Определение 4. Число а называется пределом последовательности
что этом говорят, что последовательность Приведём некоторые свойства сходящихся последовательностей. –Если последовательность имеет предел, то он единственен. –Если последовательность имеет конечный предел, то эта последовательность ограничена. –Если последовательность возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел. –Если последовательность возрастает (убывает) и не ограничена сверху (снизу), то она имеет бесконечный предел + ¥ (− ¥). 1.2. Числовой ряд. Основные понятия теории числовых рядов: Пусть задана бесконечная последовательность чисел Определение 5. Бесконечным числовым рядом называется выражение вида | ||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

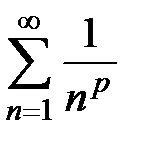 называется рядом Дирихле с показателем р,
называется рядом Дирихле с показателем р,  R. Заметим, что при
R. Заметим, что при  получаем ряд
получаем ряд  , который называется гармоническим.
, который называется гармоническим. на сходимость в зависимости от р.
на сходимость в зависимости от р.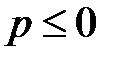 , члены ряда
, члены ряда 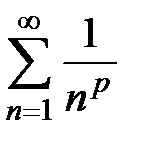 образуют неубывающую последовательность, а сам ряд расходится по необходимому признаку сходимости (
образуют неубывающую последовательность, а сам ряд расходится по необходимому признаку сходимости (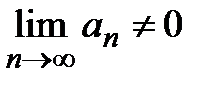 ).
). для исследования сходимости ряда используем интегральный признак Коши. Введём функцию
для исследования сходимости ряда используем интегральный признак Коши. Введём функцию  , которая удовлетворяет всем условиям теоремы Коши (теорема 3, лекция 1, разд. 1.5): при
, которая удовлетворяет всем условиям теоремы Коши (теорема 3, лекция 1, разд. 1.5): при 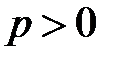 она непрерывна, положительна и монотонно убывает,
она непрерывна, положительна и монотонно убывает,  . Вычислим несобственный интеграл
. Вычислим несобственный интеграл  в двух случаях а)
в двух случаях а) 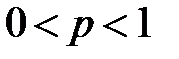 , б)
, б)  , т.е. когда
, т.е. когда  :
: 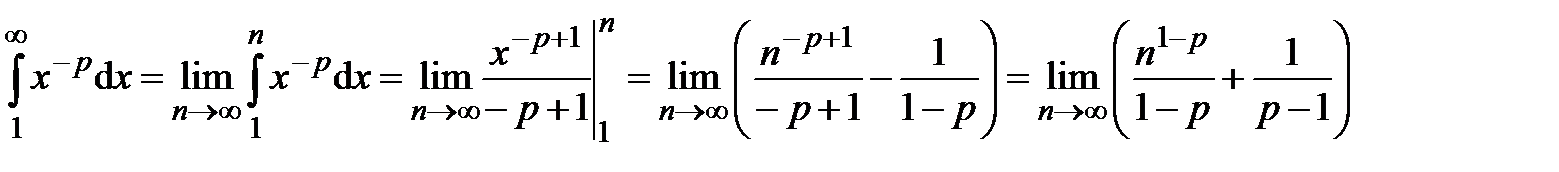
 ,
,  , то
, то  при
при  , тогда
, тогда 
 , следовательно, несобственный интеграл расходится и расходится исходный ряд.
, следовательно, несобственный интеграл расходится и расходится исходный ряд. ,
,  , то
, то  при
при  , тогда
, тогда  , следовательно, несобственный интеграл сходится и сходится исходный ряд.
, следовательно, несобственный интеграл сходится и сходится исходный ряд. имеем гармонический ряд
имеем гармонический ряд  , для которого
, для которого , следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится.
, следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится. сходится, если
сходится, если  , и расходится, если
, и расходится, если  .
. абсолютно сходится, то он абсолютно сходится при любой перестановке его членов, при этом сумма ряда не зависит от порядка расположения членов. Если
абсолютно сходится, то он абсолютно сходится при любой перестановке его членов, при этом сумма ряда не зависит от порядка расположения членов. Если  − сумма всех его положительных членов, а
− сумма всех его положительных членов, а  − сумма всех абсолютных величин отрицательных членов, то сумма ряда
− сумма всех абсолютных величин отрицательных членов, то сумма ряда  равна
равна  .
. абсолютно сходится и
абсолютно сходится и 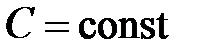 , то ряд
, то ряд  также абсолютно сходится.
также абсолютно сходится.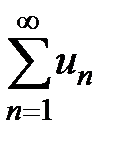 и
и  абсолютно сходятся, то ряды
абсолютно сходятся, то ряды  также абсолютно сходятся.
также абсолютно сходятся.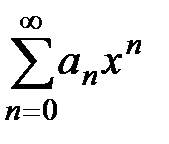 , у которого интервал сходимости
, у которого интервал сходимости  , тогда сумма степенного ряда
, тогда сумма степенного ряда  определена для всех
определена для всех  и можно записать равенство
и можно записать равенство  .
. сходится абсолютно в любом промежутке
сходится абсолютно в любом промежутке  , лежащем в интервале сходимости, причём сумма степенного ряда
, лежащем в интервале сходимости, причём сумма степенного ряда 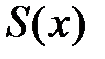 является непрерывной функцией при всех
является непрерывной функцией при всех  .
. , то степенной ряд можно
, то степенной ряд можно , то
, то .
. 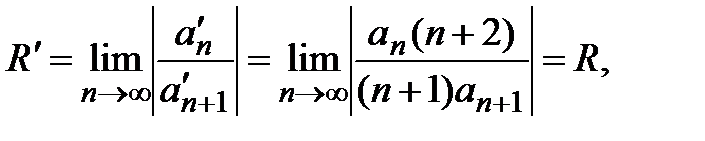
 − коэффициенты проинтегрированного ряда.
− коэффициенты проинтегрированного ряда. ,
, ,
, , …, и т.д.
, …, и т.д. определена в некоторой окрестности точки
определена в некоторой окрестности точки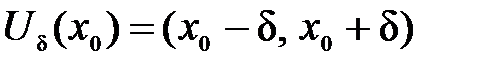 , где
, где  , причём в этой окрестности функция имеет все производные до
, причём в этой окрестности функция имеет все производные до  -го порядка.
-го порядка. по степеням
по степеням  так, чтобы в точке х 0 совпадали значения
так, чтобы в точке х 0 совпадали значения  и
и 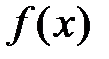 , а также значения их производных до (
, а также значения их производных до ( )-го порядка включительно. Тогда считаем, что в окрестности точки х 0 такой многочлен
)-го порядка включительно. Тогда считаем, что в окрестности точки х 0 такой многочлен  будет приближать данную функцию с некоторой точностью.
будет приближать данную функцию с некоторой точностью. являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий:
являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий: ,
,  ,
, 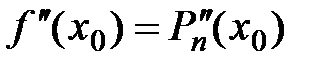 , …,
, …,  .
. :
: ,
, ,
, ,
, , при всех
, при всех  R.
R. и приравняем
и приравняем  , где
, где  :
: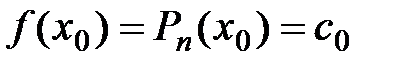 ,
,  ,
,  ,
, , …
, …  .
.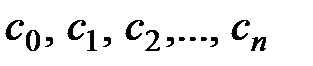 , решая полученную систему уравнений:
, решая полученную систему уравнений: .
. :
: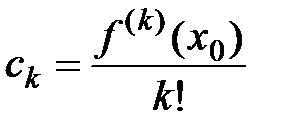 ,
,  . (4)
. (4)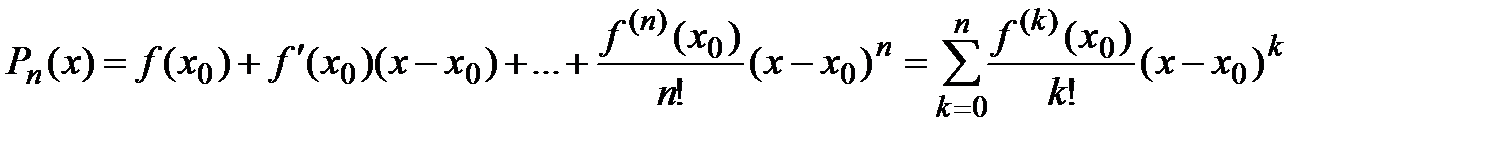 .
.
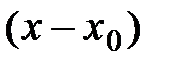 , где
, где  называются коэффициентами многочлена Тейлора,
называются коэффициентами многочлена Тейлора,  .
. , удовлетворяющей поставленным условиям при
, удовлетворяющей поставленным условиям при  , можно найти многочлен Тейлора
, можно найти многочлен Тейлора  (в точке х 0 функция
(в точке х 0 функция  совпадают со своими производными до n -го порядка).
совпадают со своими производными до n -го порядка). , обозначенную через
, обозначенную через 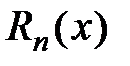 , называют остаточным членом формулы Тейлора, которая имеет вид:
, называют остаточным членом формулы Тейлора, которая имеет вид: (5)
(5) по степеням
по степеням  порядка n. Отметим, что
порядка n. Отметим, что .
. играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов.
играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов. называется бесконечно малой при
называется бесконечно малой при  , если
, если  .
.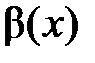 называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции
называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции  при
при  , если существует
, если существует  и записывается следующим образом:
и записывается следующим образом:  (что читается так: «β есть о малое от α).
(что читается так: «β есть о малое от α).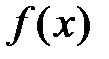 по степеням
по степеням 
 . Остаточный член в формуле Тейлора имеет вид:
. Остаточный член в формуле Тейлора имеет вид:  . Из построения многочлена Тейлора следует
. Из построения многочлена Тейлора следует  Тогда
Тогда 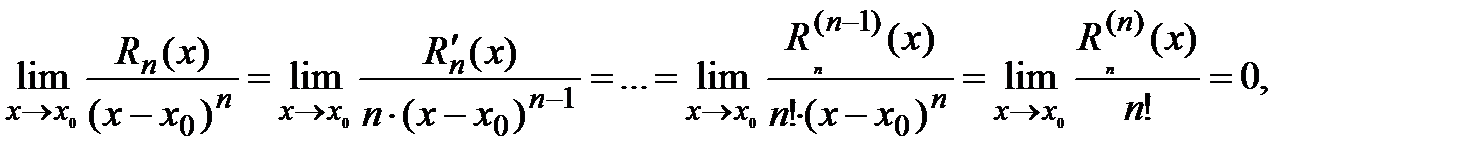 откуда остаточный член формулы Тейлора можно записать в виде:
откуда остаточный член формулы Тейлора можно записать в виде:  , т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно
, т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно  при
при  .
. , в которой
, в которой  ,
,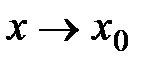 является бесконечно малой величиной, то можно считать, что разность
является бесконечно малой величиной, то можно считать, что разность  бесконечно мала, т.е.
бесконечно мала, т.е. 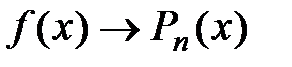 .
. , где Q (x) есть некоторая функция, подлежащая определению. Можно доказать, что
, где Q (x) есть некоторая функция, подлежащая определению. Можно доказать, что  , где точка ξ заключена между х и х 0:
, где точка ξ заключена между х и х 0: 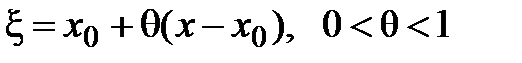 , т.е. остаточный член имеет вид:
, т.е. остаточный член имеет вид:  . Тогда формула Тейлора примет вид
. Тогда формула Тейлора примет вид  , который называется формулой Тейлора с остаточным членом в форме Лагранжа.
, который называется формулой Тейлора с остаточным членом в форме Лагранжа. , то получаем формулу конечного приращения:
, то получаем формулу конечного приращения: 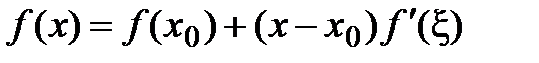 (теорема Лагранжа).
(теорема Лагранжа). , то получим формулу, которую называют формулой Маклорена:
, то получим формулу, которую называют формулой Маклорена: ,
,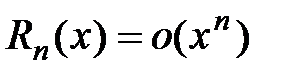 или в форме Лагранжа:
или в форме Лагранжа: .
. в виде многочлена по степеням х.
в виде многочлена по степеням х.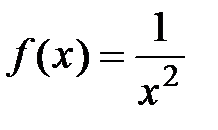 в виде многочлена третьего
в виде многочлена третьего с остаточным членом в форме Лагранжа.
с остаточным членом в форме Лагранжа. в точке
в точке  в
в ,
, .
. :
: ,
,  ;
;  ,
,  ;
;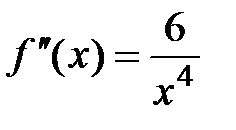 ,
,  ;
; 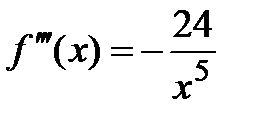 ,
,  ;
; 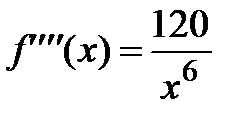 ,
,  , где
, где 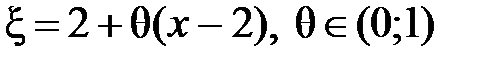 .
. и вычисляем
и вычисляем 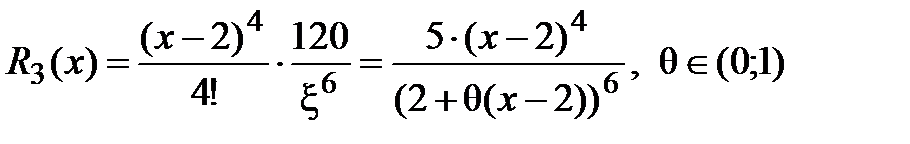 .
.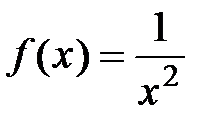 заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора
заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора  при
при  .
. ,
,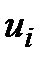 члены ряда,
члены ряда, 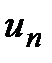 – n-й или общий член ряда, называется бесконечным рядом.
– n-й или общий член ряда, называется бесконечным рядом. , (1)
, (1)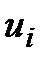 называемые членами ряда, образуют бесконечную последовательность; член
называемые членами ряда, образуют бесконечную последовательность; член  называется общим членом ряда.
называется общим членом ряда.

 стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е. и
и  .
. .
. или
или  ), то такой ряд называется расходящимся.
), то такой ряд называется расходящимся. 2)
2)  3)
3)  4)
4)  5)
5) 
 7)
7)  8)
8)  9)
9) 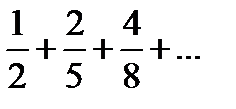 10)
10) 
 где p>0, называется рядом Дирихле. Этот ряд сходится при
где p>0, называется рядом Дирихле. Этот ряд сходится при 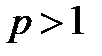 и расходится при
и расходится при  . Частным случаем ряда Дирихле (при
. Частным случаем ряда Дирихле (при  ) является гармонический ряд
) является гармонический ряд  .
.


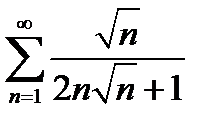






 выполняется условие
выполняется условие  то ряд сходится при
то ряд сходится при  и расходится при
и расходится при 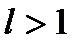 .
. . В этом случае для исследования ряда применяются другие признаки.
. В этом случае для исследования ряда применяются другие признаки.


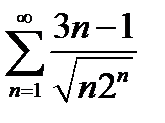






 , где
, где  = f(n), n ≥1 сходится или расходится
= f(n), n ≥1 сходится или расходится
 2)
2)  3)
3)  4)
4)  5)
5) 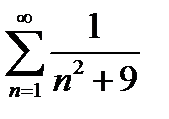
 7)
7)  8)
8)  9)
9)  10)
10) 
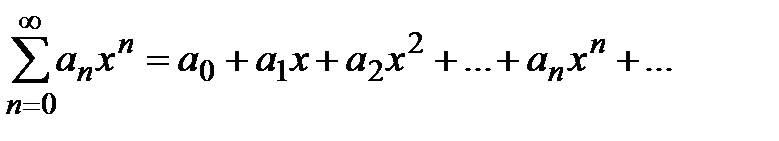 .
. , при которых данный ряд сходится.
, при которых данный ряд сходится. ряд сходится и притом абсолютно, а при
ряд сходится и притом абсолютно, а при 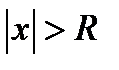 ряд расходится. Радиус сходимости найдем, используя признак Даламбера:
ряд расходится. Радиус сходимости найдем, используя признак Даламбера:
 , удовлетворяющих данному условию и расходится при
, удовлетворяющих данному условию и расходится при  . Отсюда следует, что если существует предел
. Отсюда следует, что если существует предел  ,то радиус сходимости ряда
,то радиус сходимости ряда  равен этому пределу и степенной ряд сходится при
равен этому пределу и степенной ряд сходится при 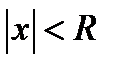 , т.е. в промежутке
, т.е. в промежутке  , который называется промежутком (интервалом) сходимости.
, который называется промежутком (интервалом) сходимости.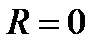 , то степенной ряд сходится в единственной точке
, то степенной ряд сходится в единственной точке 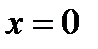 . На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.
. На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться. и
и  исследуется с помощью какого-либо из признаков сходимости.
исследуется с помощью какого-либо из признаков сходимости.
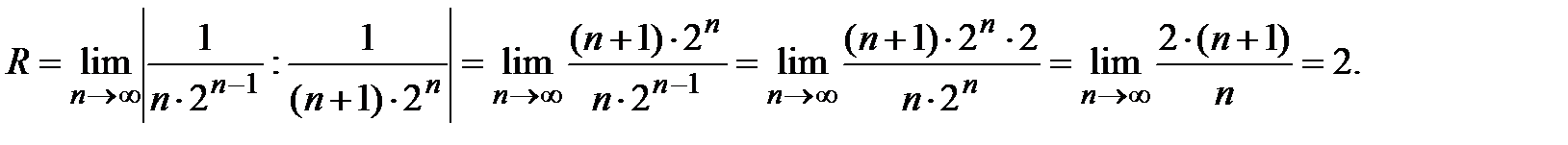
 , т.е. при
, т.е. при  . При
. При  имеем ряд
имеем ряд  , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница. имеем расходящийся ряд:
имеем расходящийся ряд: 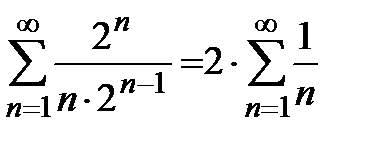 . Ответ: областью сходимости исходного ряда является промежуток
. Ответ: областью сходимости исходного ряда является промежуток  Задание 7. Найти область сходимости степенного ряда:
Задание 7. Найти область сходимости степенного ряда: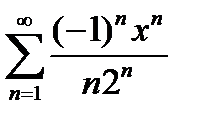





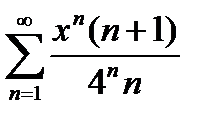

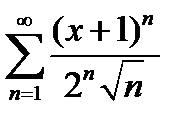
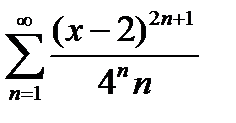
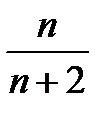 , 2)
, 2)  , 3)
, 3)  , 4), 5)
, 4), 5) 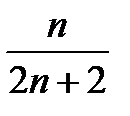 , 6)
, 6)  , 7)
, 7)  ,
,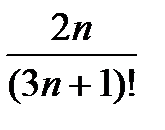 , 9)
, 9) 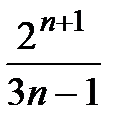 , 10)
, 10) 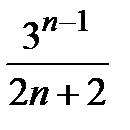 .
. , 3)
, 3) 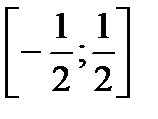 , 4) (-4;4), 5) [-3;1), 6) [-1;5], 7) (-6;2), 8) (-2;1), 9)
, 4) (-4;4), 5) [-3;1), 6) [-1;5], 7) (-6;2), 8) (-2;1), 9) 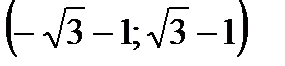 , 10) (0;4).
, 10) (0;4).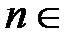 N поставлено в соответствие (по определённым правилам) определённое действительное число
N поставлено в соответствие (по определённым правилам) определённое действительное число 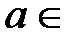 R; тогда множество упорядоченных действительных чисел
R; тогда множество упорядоченных действительных чисел  называется числовой последовательностью и обозначается
называется числовой последовательностью и обозначается 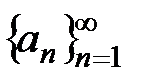 , где
, где  − общий член последовательности. Например, последовательность
− общий член последовательности. Например, последовательность  имеет общий член
имеет общий член  , где
, где  N.
N. называется убывающей, если
называется убывающей, если  N, и возрастающей, если
N, и возрастающей, если  N.
N. называется ограниченной сверху, если существует такое число М,
называется ограниченной сверху, если существует такое число М,  R, что
R, что  N, и ограниченной снизу, если существует такое число М,
N, и ограниченной снизу, если существует такое число М,  N.
N. называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М > 0
называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М > 0 R), что
R), что  .
. ,
,
 N, зависящий от
N, зависящий от  выполняется неравенство
выполняется неравенство  . Тогда
. Тогда  означает,
означает,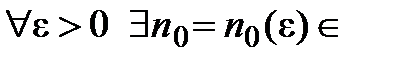 N такое, что для всех
N такое, что для всех 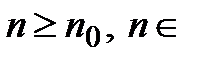 N:
N:  . При
. При сходится к числу а.
сходится к числу а. R.
R. , обозначаемое как
, обозначаемое как 


