
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разделяя переменные, получимСодержание книги
Поиск на нашем сайте
Интегрируя, найдем
или
Заменяя u через
30. Кривая проходит через точку (1,1). Расстояние до любой касательной к этой кривой от начала координат равно абсциссе точки касания. Составить уравнение указанной кривой. Решение. Пусть точка (х,у) лежит на указанной кривой у=у(х). Касательная к этой кривой, проведенная в точке (х,у), находится от начала координат на расстоянии
которое по условию задачи равно х. Поэтому указанная кривая является решением уравнения
или
Это однородное уравнение. Решим его, полагая y=xu:
Согласно замене D. Ответы.
7. Рекомендуемая литература
1. Бугров Я.С., Никольский С.М.: Дифференциальное и интегральное исчисление. М. Высшая школа, 1993.
6. Кудрявцев Л.Д.: Курс математического анализа. М. Высшая школа, 1998.
Итоговая аттестация Вопросы к экзамену по дисциплине “Математический анализ”. 1. Числовые множества. Множества N и Z. Операции сложения и умножения в этих множествах и их свойства. 2. Множества Q и R. Свойства арифметических операций в этих множествах. 3. Кванторы существования и общности, их значение и применение в записи математических выражений. Ограниченные и неограниченные множества. Точные грани числовых множеств. 4. Операции над множествами. Объединение, пересечение и дополнение множеств. 5. Понятие числовой последовательности. Способы задания числовой последовательности. 6. Понятие предела последовательности. Сходящиеся и расходящиеся последовательности. 7. Определение предела числовой последовательности. Единственность предела. 8. Свойства сходящихся последовательностей. Ограниченные числовые последовательности и их свойства. 9. Способы вычисления пределов последовательностей (с примером). 10. График функции. Преобразование графиков функций. 11. Монотонные числовые последовательности. Точная верхняя и нижняя грани числовой последовательности. 12. Необходимое и достаточное условие сходимости числовой последовательности (критерий Коши). 13. Определение функции. Способы задания функций. Композиция функций. 14. Точки экстремума. Необходимое и достаточное условия существования экстремума в точке. 15. Ограниченные и неограниченные функции. Функции, ограниченные сверху и ограниченные снизу. Монотонные функции. 16. Сложная функция. Понятие обратной функции и условие ее существования. 17. Неявно заданные функции. Функции, заданные параметрически. 18. Определение предела функции по Коши. Другие определения предела. Их эквивалентность. 19. Различные типы пределов функции. Односторонние конечные пределы функции в точке. Бесконечные пределы функции в конечной точке. 20. Различные типы пределов функции. Односторонние бесконечные пределы в точке. Конечный предел функции в бесконечности. 21. Локальные свойства функции, имеющей предел. Ограниченность функции, имеющей предел в точке. Знакопостоянство функции в окрестности предельной точки. 22. Свойства функций, имеющих предел, связанные с арифметическими операциями над ними. Теоремы о пределах. 23. Бесконечно малые функции. Их связь с бесконечно большими. Свойства бесконечно малых функций. 24. Теорема о существовании предела монотонной функции на отрезке. Свойства функции, непрерывной на отрезке. 25. Понятие непрерывности функции в точке. Определение непрерывности. Непрерывность функции в точке справа и слева. 26. Точки разрыва функции и их классификация. 27. Нахождение точек разрыва функций. Локальные свойства непрерывных функций. 28. Сравнение бесконечно малых функций. Эквивалентные бесконечно малых функций и их использование при вычислении пределов. 29. Первый и второй замечательный пределы (один с выводом). Их применение при вычислении пределов. 30. Сравнение бесконечно малых функций. Критерий определения бесконечно малой более высокого порядка, Понятие производной функции. Геометрический и физический смысл производной. Понятие односторонней производной. 31. Уравнение касательной и нормали к графику функции. 32. Определение дифференциала функции. Геометрический смысл дифференциала. 33. Правила дифференцирования функций (одно с выводом). 34. Дифференцирование функций, заданных неявно. Дифференцирование функций, заданных параметрически. 35. Инвариантность формы первого дифференциала. Производные и дифференциалы высших порядков. 36. Дифференцирование сложной функции. Теорема о дифференцировании обратной функции. 37. Теорема Ферма (с доказательством). 38. Теорема Ролля (с доказательством). 39. Теорема Лагранжа (с доказательством). 40. Теорема Коши. Правило Лопиталя и его применение к нахождению пределов функций. 41. Логарифмическое дифференцирование. Привести пример. 42. Наибольшее и наименьшее значения функции на отрезке. 43. Точки перегиба. Достаточное условие существования точки перегиба. 44. Промежутки выпуклости и вогнутости. 45. Асимптоты графика функции. 46. Общая схема исследования функции. 47. Числовые ряды. Частичная сумма ряда. Сходящиеся и расходящиеся ряды. Необходимый признак сходимости ряда. 48. Основные признаки сходимости рядов (с примером). 49. Знакочередующиеся и знакопеременные ряды. Признаки их сходимости (с примером). 50. Функциональные ряды. Степенные ряды. Радиус, интервал и область сходимости. 51. Теорема Тейлора. Формула Маклорена. Разложение элементарных функций в ряды Тейлора и Маклорена. 52. Понятие первообразной. Неопределённый интеграл и его основные свойства. 53. Таблица основных интегралов. 54. Основные методы интегрирования. Способ замены переменной. 55. Основные методы интегрирования. Интегрирование по частям (с примером). 56. Основные методы интегрирования. Интегрирование рациональных дробей (с примером). 57. Основные методы интегрирования. Интегрирование тригонометрических функций (с примером). Универсальная тригонометрическая подстановка. 58. Основные методы интегрирования. Нахождение интегралов от иррациональных выражений (с примером). 59. Определённый интеграл. Основные свойства, условие существования. 60. Способы вычисления определённого интеграла. Формула Ньютона-Лейбница. Замена переменной в определённом интеграле. Интегрирование по частям. 61. Геометрический и физический смысл определённого интеграла. 62. Приложения определённого интеграла. Вычисление площадей фигур в декартовых координатах. 63. Приложения определённого интеграла. Вычисление объёмов тел по известным поперечным сечениям. Объёмы тел вращения. 64. Приложения определённого интеграла. Длина дуги плоской кривой. Площадь поверхности вращения. 65. Приближённое вычисление определённых интегралов. Формулы прямоугольников, трапеций и Симпсона. 66. Несобственные интегралы. Интегралы с бесконечными пределами. 67. Несобственные интегралы. Интегралы от разрывных функций. Признаки сходимости несобственных интегралов. 68. Системы координат в пространстве. Функция двух переменных: способы задания, геометрическое представление. Функции более двух независимых переменных. 69. Предел функции двух переменных. 70. Понятие области. Замкнутые и ограниченные области. Точки и линии разрыва. 71. Непрерывность функции двух переменных. Функции, непрерывные в замкнутой области. 72. Частные производные 1– го порядка. Частные производные высших порядков. 73. Полное приращение и полный дифференциал функции двух переменных. 74. Геометрический смысл полного дифференциала. Приближённые вычисления с помощью дифференциала. Дифференциалы высших порядков. 75. Производная по направлению. 76. Градиент функции и его геометрический смысл. 77. Касательная плоскость и нормаль к поверхности. 78. Локальный экстремум функции двух переменных. Необходимое условие экстремума. Достаточные условия экстремума. 79. Глобальный экстремум функции двух и нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой области. 80. Условный экстремум функции двух переменных. Примеры практических заданий к экзамену по дисциплине “Математический анализ”.
1. Найти предел последовательности: 2. Найти предел последовательности: 3. Найти предел последовательности: 4. Найти предел последовательности: 5. Найти предел функции: 6. Найти предел функции: 7. Найти предел функции: 8. Найти предел функции: 9. Найти предел функции: 10. Найти предел функции: 11. Исследовать функцию и построить ее график: 12. Исследовать функцию и построить ее график: 13. Исследовать функцию и построить ее график: 14. Исследовать функцию и построить ее график: 15. Исследовать функцию на непрерывность: 16. Исследовать функцию на непрерывность: 17. Найти наибольшее и наименьшее значения функции 18. Найти наибольшее и наименьшее значения функции 19. Найти наибольшее и наименьшее значения функции 20. Исследовать ряд на сходимость: 21. Исследовать ряд на сходимость: 22. Исследовать ряд на сходимость: 23. Исследовать ряд на сходимость: 24. Исследовать ряд на сходимость: 25. Найти радиус, интервал и область сходимости ряда: 26. Найти радиус, интервал и область сходимости ряда: 27. Найти радиус, интервал и область сходимости ряда: 28. Найти неопределённый интеграл: 29. Найти неопределённый интеграл: 30. Найти неопределённый интеграл: 31. Найти неопределённый интеграл: 32. Найти неопределённый интеграл: 33. Найти неопределённый интеграл: 34. Найти определённый интеграл: 35. Найти определённый интеграл: 36. Найти определённый интеграл: 37. Вычислить площадь фигуры, ограниченной линиями: 38. Вычислить площадь фигуры, ограниченной линиями: 39. Вычислить площадь фигуры, ограниченной линиями: 40. Найти производные 1-го и 2-го порядков функции: 41. Найти производные 1-го и 2-го порядков функции: 42. Найти полный дифференциал функции: 43. Найди градиент функции z в точке М: 44. Исследовать функцию на экстремум: 9. Типовые варианты контрольных работ.
Контрольная работа №1
6. Укажите для функции
7. Найдите предел, используя правило Лопиталя: 8. Найдите значения A и B, при которых функция f(x) является бесконечно малой
9. Если Контрольная работа №2 1. Найти предел
2. Докажите, используя определение предела функции в точке, что функция 3. Укажите для функции
4. Найдите производные
5. Исследуйте на экстремум функцию:
6. Найти экстремум функции Решить задачу с помощью введения функции Лагранжа. Нарисовать · график условия, · изолинии, проходящие через стационарные точки функции Лагранжа, · градиент в этих точках. 7. Спрос
Контрольная работа №3 1. Найдите интегралы:
2. Исследовать ряды на сходимость:
3. Исследовать на сходимость интеграл
4. Найти производную функции Типовой вариант экзаменационной контрольной работы 1. Найти предел 2. Найти интеграл 3. Найти область сходимости ряда 4. Найти экстремум функции Решить задачу с помощью введения функции Лагранжа. Нарисовать · график условия, · изолинии, проходящие через стационарные точки функции Лагранжа, · градиент функций 5. Расставить пределы интегрирования в том и другом порядке, преобразовав интеграл в повторный если область
6. Спрос 9. Материально-техническое обеспечение дисциплины: Специально оборудованные кабинеты и аудитории: компьютерные классы, аудитории, оборудованные мультимедийными средствами обучения. 10. Методические рекомендации по организации изучения дисциплины: Контроль знаний студентов включает формы текущего и итогового контроля. Текущий контроль осуществляется в виде контрольной работы и домашнего задания. Итоговый контроль осуществляется в виде зачетной контрольной работы и письменного экзамена. Для оценки качества освоения дисциплины можно использовать задачи (более 4000 по всем разделам курса), приведенные в задачнике: Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1997.
Разработчики: ___ ГУ ВШЭ _______ д. т.н., профессор ___ Ф.Т. Алескеров __ (место работы) (занимаемая должность) (инициалы, фамилия)
___ ИПУ РАН ______ __ д. ф.-м. наук_______ (место работы) (занимаемая должность) (инициалы, фамилия)
Эксперты: _____ МГУ___ _____ ___ профессор ___ ___ А.А. Васин___ __ (место работы) (занимаемая должность) (инициалы, фамилия)
_____ ВЦ РАН___ __ ___ профессор ___ ___ А.В. Лотов___ __ (место работы) (занимаемая должность) (инициалы, фамилия)
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.008 с.) |




 , получаем общий интеграл данного уравнения
, получаем общий интеграл данного уравнения
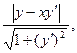
 ,
, т.е.
т.е.

 , получим y2+x2=Cx. По условию кривая проходит через точку (1,1): 1+1=С, т.е. С=2. Таким образом, уравнение искомой кривой x2+y2=2x, или
, получим y2+x2=Cx. По условию кривая проходит через точку (1,1): 1+1=С, т.е. С=2. Таким образом, уравнение искомой кривой x2+y2=2x, или 


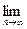











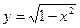

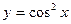


 на отрезке [-1; 3].
на отрезке [-1; 3]. на отрезке [-2; 2].
на отрезке [-2; 2]. на отрезке [-1;1].
на отрезке [-1;1].




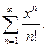

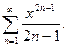





 .
.
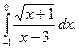

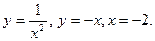






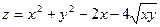


 :
:
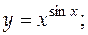 4.
4. 

 эквивалентную функцию вида
эквивалентную функцию вида  :
: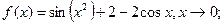

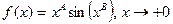 .
.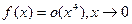 , то верно ли, что
, то верно ли, что  .
.
 непрерывна в точке
непрерывна в точке  .
. при
при  ;
; .
. и
и  функции
функции  , заданной параметрически:
, заданной параметрически: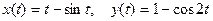 .
.
 при условии
при условии  .
. и предложение
и предложение  зависят от цены
зависят от цены  следующим образом:
следующим образом:  ,
,  . Найти наибольшее значение дохода и определить эластичность функции дохода в точке максимума.
. Найти наибольшее значение дохода и определить эластичность функции дохода в точке максимума. ;
;
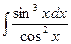 ;
;
 ;
;
 ;
;
 ;
;







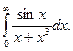

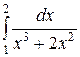 .
. .
. .
. и
и  в этих точках.
в этих точках. ,
, ограничена линиями:
ограничена линиями:  ;
;  ;
;  .
.


