
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательности и их представления.Содержание книги Поиск на нашем сайте
Последовательности и их представления.
Дискретные сигналы определяются для дискретных значений независимой переменной - времени. Время квантуется обычно равномерно:
T=nT;
Где Т – интервал между отсчетами n – целые числа, -5, -4, -3,…, 0, 1, 2, 3,… Обозначения последовательностей:
1. {h(n)},
2. {h(nT)},
3. h(n),
4. h(nT),
1 и 3 – Применяются при неравномерном распределении отсчетов. 2 и 4 – Применяются при равномерном расположении отсчетов.
Способы получения последовательностей.
1)
Взять набор чисел и расположить их в виде последовательности – 0,1,2,3,…,(N-1) Это образует последовательность: 2) Использование рекуррентного соотношения:
h(n)=h(n-1)/2
С начальным условием h(0)=1
Это последовательность:
3) Взять отсчеты равноотстоящие из непрерывного сигнала, т.е. положить.
где Т – интервал дискретизации.
Для получения такой последовательности используется
АЦП – аналого-цифровой преобразователь.
Графические изображения последовательностей:
1 – элемент последовательности, изображающийся отрезком соответствующей длины. 2 – Изображается только огибающая последовательности.
Некоторые важные последовательности.
1)
Цифровой единичный импульс (единичный отсчет)
Его роль такая же, как аналоговый единичный импульс (дельта функция Дирака) в аналоговых системах.
- обобщенная функция или распределение.
2) Единичный скачок:
Единичный скачок выражается через единичный импульс:
3) Убывающая экспонента.
4) Косинусоида
5) Комплексная экспонента
Для ее изображения необходимы раздельные графики вещественной и мнимой части. Можно изобразить в виде вектора, вращающегося с частотой омега.
Многие из этих последовательностей играют важную роль в теории цифровой обработки сигналов.
Представление произвольных последовательностей.
Рассмотрим последовательность а(0), а(1), а(2), …, а(n);
где а(n) – величина n-го элемента.
Такую последовательность можно представить:
Дискретная система.
y(n)=Ф[x(n)]
Линейная система.
x1(n) y1(n)
x2(n) y2(n)
Тогда, если на входе
ax1(n)+bx2(n), а на выходе будет. ay1(n)+by2(n), то система называется линейной.
Система с постоянными параметрами (ЛПП).
x(n) y(n)
x(n-n0) y(n-n0) – при любых n0
где n0 – величина задержки.
Тогда:
Из свойств линейности:
Откликом системы на
Должна быть последовательность
Поэтому отклик на x(n) будет равен:
Заменой переменной можно представить.
Это уравнение представляет собой цифровую свертку. Т.О., чтобы вычислить выходную последовательность системы на заданную входную, необходимо вычислить цифровую свертку входной последовательности и импульсной характеристики системы.
Физическая реализуемость. ЛПП – система физически реализуема, если отклик при n=n0 зависит только от отсчетов входной последовательности с номерами Это означает, что импульсная характеристика h(n) системы равна нулю, при всех
Примеры систем физически нереализуемых. - Идеальный ФНЧ - Идеальный дифференциатор.
Устойчивость ЛПП.
Если при любой ограниченной входной последовательности выходная последовательность так же ограничена.
Необходимое и достаточное условие.
Устойчивость системы:
(*)
Доказательство необходимости.
Пусть (*) не удовлетворяется:
Рассмотрим входную последовательность.
Т.о. последовательность y (0) не ограничена, так, что неравенство (*) является необходимым условием устойчивости. Доказательство достаточности.
Пусть (*) выполняется. На вход поступает ограниченная последовательность Тогда:
Последовательность y(n) ограничена, поэтому система устойчива, что и требовалось доказать.
Примеры импульсных характеристик.
1) Пример устойчивой системы.
2) Пример неустойчивой системы.
Разностные уравнения. В общем виде линейное разностное уравнение М-го порядка с постоянными коэффициентами имеет вид:
Разностные уравнения – это алгоритм функционирования системы. Зная входную последовательность x(m) и начальные условия: x(n-1), x(n-2), …, y(n-1), y(n-2), … Всегда можно определить соответствующую ей выходную последовательность y(n).
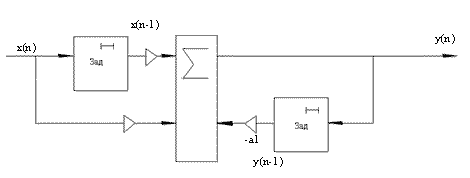
Рассмотрим разностное уравнение первого порядка.
Элемент задержки осуществляет задержку последовательности на один отсчет.
Разностное уравнение второго порядка:
Схема имеет вид:
Частотная характеристика.
При подаче на вход последовательностей вида:
На выходе ЛПП - систем последовательность y(n) будет совпадать с входной, умноженной на некоторый комплексный коэффициент, зависящий только от частоты гармонического сигнала.
Выходная последовательность:
Множитель называется частотной характеристикой ЛПП – систем, т.к. он представляет коэффициент передачи ЛПП – систем для каждого значения частоты.
Пример:
Частотная характеристика:
Т.к.
Свойства частотной характеристики: 1. Частотная характеристика является периодической функцией. 2. 3. 4. Для действительных h(n) (что часто бывает на практике) модуль
5. Поэтому часто частотную характеристику задают на интервале
Дискретный ряд Фурье
Рассмотрим частотную характеристику системы с импульсной характеристикой h(n):
(*)
(**) Т.о. эти два равенства (*) и (**) представляют собой пару преобразований Фурье. h(n) – суперпозиция синусоид Для произвольной входной последовательности x(n):
И
Можно показать, что:
Ранее получали:
Т.о. отклик системы во временной области y(n) есть цифровая свертка импульсной характеристики h(m) и входной последовательности x(n) или В частотной области: преобразование Фурье от выходной последовательности
Единицы измерения частоты Запись: x(n), y(n), h(n) - опускается период дискретизации Т или Тогда запись:
Функция Если записать: x(nT), y(nT), h(nT) - где Т – период дискретизации,
Тогда запись:
Или можно выразить:
Тогда частота f – измеряется в Герцах (Гц).
Свойства ДПФ 1. Линейность xp(n) и yp(n) – периодичные последовательности с периодом N каждая. Xp(к) и Yp(к) – их ДПФ. Тогда для последовательности: xp(n)+yp(n) ДПФ будет равно: Xp(к)+Yp(к) Это положение справедливо и для последовательностей конечной длины.
2. Сдвиг xp(n) c периодом N тогда для xp(n-n0) 3. Свойство симметрии Если xp(n) периодическая последовательность в N отсчетов и является действительной, то ее ДПФ удовлетворяет условиям симметрии:
Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-течное ДПФ X(k). Если будет дополнительное условие симметрии:
то окажется, что Примечание: вычислив одно ДПФ можно получить ДПФ двух последовательностей. xp(n) и yp(n) – действительные последовательности с периодом N отсчетов. Рассмотрим последовательность комплексную:
Ее ДПФ равно:
Действительные части
Если эти две последовательности x(n) и y(n) являются еще и симметричными, то можно сократить еще большее число операций. Нерекурсивные цифровые фильтры.
Порядок расчета фильтров. Свойства КИХ-фильтров. Характеристики КИХ-фильтров с ЛФХ. Частотные характеристики КИХ-фильтров с ЛФХ.
Свойства КИХ-фильтров.
Основные достоинства этих фильтров: 1) Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой. (Линейная фазовая характеристика особенно важна при обработке речевых сигналов, изображений, а также передаче данных). 2) КИХ-фильтры можно эффективно строить как по рекурсивной, так и по нерекурсивной схемам. 3) КИХ-фильтры, реализуемые нерекурсивно, всегда устойчивые. 4) Нерекурсивные КИХ-фильтрыпозволяют минимизировать шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью (разрядностью).
Недостатки КИХ-фильтры: 1) Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Поэтому при реализации необходимо выполнять большой объем вычислений.
2) Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации.
Прямоугольное окно N-точечное прямоугольное окно Весовая функция
Предполагается, что N – четное для простоты. Частотная характеристика – преобразование Фурье:
можно получить:
Метод взве шивания Т.к. частотная характеристика ЦФ – периодическая функция частоты, ее можно представить рядом Фурье: (*)
Коэффициенты ряда Фурье, т.е. h(n) – совпадает с коэффициентами импульсной характеристики ЦФ.
Трудности использования соотношения (*): 1) Импульсная характеристика h(n) – получается имеет бесконечную длину, т.к. суммирование в пределах 2) Фильтр – физически нереализуем,. Т.к. h(n) начинается в
Один из методов получения КИХ-фильтра, аппроксимирующего заданную функцию Однако простое усечение ряда приводит к хорошо известному явлению Гиббса, которое проявляется в виде выбросов и пульсаций до и после разрывов в аппроксимируемой частотной характеристике и в увеличении переходной полосы. Простое увеличение числа отсчетов h(n), т.е. увеличение M, не всегда приводит к желаемому результату, хотя иногда это приводит к улучшению аппроксимации частотной характеристики. Лучшие результат дает метод, основанный на использовании весовой последовательности конечной длины a(n), называемой окном, для модификации коэффициентов Фурье h(n) в формуле (*) с тем, чтобы управлять сходимостью ряда Фурье.
Вывод: с увеличением N – уменьшается полоса пропускания ФНЧ. Нельзя получить боковой лепесток с подавлением больше чем –13 дБ.
Обобщенное окно Хэмминга Окно имеет вид:
Если Частотная характеристика:
Выводы: 1) Ширина главного лепестка частотной характеристики окна Хэмминга в 2 раза больше, чем для прямоугольного окна. 2) Уровень боковых лепестков в случае окна Хэмминга значительные ниже, чем у характеристики прямоугольного окна. Так при
Окно Кайзера Задача расчета хороших окон практически сводится к математической задаче отыскания ограниченных во времени функций преобразования Фурье которых наилучшим образом аппроксимируют функции, ограниченные по частоте, т.е. имеют минимальную энергию за пределами заданного интервала частот. Для решения этих задач в непрерывном времени был введен класс так называемых вытянутых сфероидальных волновых функций. Эти функции имеют сложный вид. Кайзер – для их аппроксимации ввел окно, которое называется окном Кайзер:
Здесь
Частотная характеристика дискретного окна Кайзера в замкнутом виде не получена.
Окно Кайзера является по существу оптимальным в том смысле, что оно представляет последовательность конечной длины, которая имеет минимум энергии спектра за пределами некоторой заданной частоты.
ФНЧ с различными окнами
Рассмотрим идеальный фильтр нижних частот. Будем использовать 3 окна: - прямоугольное - Хэмминга - Кайзера (в каждом по n=257 отсчетов)
Коэффициенты ряда Фурье:
Частотные характеристики:
Метод частотной выборки (2-й метод)
Метод частотной выборки Это второй метод проектирования КИХ-фильтров. КИХ-фильтр может быть однозначно задан как коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ от импульсной характеристики {H(k)}, т.е. Они связаны соотношениями: (*) (**) Кроме того:
Тогда можно получить следующее выражение:
меняя порядок суммирования, получим:
Т.к.
Необходимо: 1) Произвести дискретизацию по частоте непрерывной частотной характеристики в N равноотстоящих точках, т.е. взять частотную выборку. Получаемая при этом интерполяционная формула для расчета частотной характеристики фильтра в функции непрерывной частоты имеет вид:
т.е. частотная характеристика фильтра является линейной комбинацией частотных отсчетов интерполирующих функций.
со значениями отсчетов H(k) в качестве коэффициентов.
Недостаток: Необходима дальнейшая оптимизация коэффициентов фильтра для улучшения частотной характеристики.
Метод частотной выборки (2-й метод). Свойства БИХ-фильтров(АЧХ, фазовая характеристика и групповая задержка). Методы расчета коэффициентов БИХ-фильтров. Расчет БИХ-фильтров по аналоговым прототипам. Метод отображения. Свойства БИХ-фильтров. БИХ-фильтры – это цифровые фильтры с бесконечной импульсной характеристикой, при условии, что фильтры являются физически реализуемы:
Форма записи Z-преобразования импульсной характеристики БИХ-фильтров имеет вид: (*) здесь по крайней мере хотя бы один из коэффициентов аi отличен от нуля. Фильтр с передаточной эарактеристикой (*) имеет конечное число нулей (М) и полюсов (N). Нули H(z) могут располагаться на всей z-плоскости, но полюсы H(z) в соответствии с условием устойчивости фильтра обязаны находиться внутри круга единичного радиуса. В большинстве случаев, особенно при расчете цифровых фильтров по характеристикам аналоговых фильтров, (M)
Такие системы (или фильтры) называются системами (или фильтрами) N-го порядка. В отличие от КИХ-фильтров устойчивые, физически реализуемые БИХ-фильтры не обладают строго линейной фазовой характеристикой.
Фильтры второго типа.
где Ωr - наименьшая частота, на которой достигается заданный уровень ослабления.
Фильтры второго типа имеют и полюсы и нули.
Фильтры Чебышева 1 и 2 типов определяются любыми из четырех параметров.
1. n – порядок фильтра. 2. ε - параметр, характеризующий пульсации в полосе пропускания. 3. Ωr – наименьшая частота в полосе не пропускания, достигающая заданного ослабления. 4. А – параметр, характеризующий ослабления в полосе пропускания.
Порядок фильтра определяется:
где
Пример:
Получим:
Эллиптические фильтры.
Характеризуются тем, что их амплитудная характеристика имеет равновеликие пульсации в полосе пропускания и в полосе не пропускания. Можно показать, что с точки зрения минимальной ширины переходной полосы эллиптические фильтры являются оптимальными, т.е. для заданных порядка фильтра и уровней пульсации не существует других фильтров с более быстрым переходом от полосы пропускания к полосе не пропускания.
где Rn (Ω,L) - рациональная функция Чебышева. L – параметр, характеризующий пульсации функции Rn (Ω,L)
Переходное отношение:
где Ωp – граничная частота полосы пропускания, а Ωs – граничная частота полосы непропускания. Если ввести параметр K1, равный
то порядок фильтра эллиптического, удовлетворяющего условию заданных значений ε, A, Ωp, Ωs, рассчитывается по формуле:
где K (▪) – полный зллиптический интеграл 1-го рода.
Существуют расчетные диаграммы – по проектированию фильтров нижних частот рассмотренных аппроксимаций (Б,Ч,Э)
Частотные преобразования. Прямые методы расчета цифровых БИХ – фильтров (расчет по квадрату амплитудной характеристики, расчет во временной области). Методы оптимизации при расчете БИХ – фильтров (Минимизация среднеквадратической и Lp – ошибок, оптимизация в W – плоскости с использованием всепропускающих цепей, расчет методом линейного рограммирования).
Частотные преобразования.
Рассмотрим методы расчета ФНЧ непрерывных во времени, а так же методы их дискретизации. При расчете цифровых фильтров ВЧ, ПФ и режекторных, используются два подхода:
1. - Расчет аналогичного ФНЧ - Преобразование полосы частот - Дискретизация фильтра Получаем цифровой фильтр с заданными характеристиками.
2. - Расчет аналогичного ФНЧ - Дискретизация фильтра - Преобразование полосы частот. Получаем цифровой фильтр с заданными характеристиками.
Преобразование полосы частот аналоговых фильтров.
ФНЧ ФНЧ
ФНЧ ФВЧ
ФНЧ ППФ
ФНЧ ПЗФ
где
Преобразование полосы для ЦФ.
В ФВЧ, ППФ и ПЗФ
ФНЧ в ФНЧ
где
ФНЧ в ФВЧ
где
ФНЧ в ППФ
где
ФНЧ в ПЗФ
где
Прямые методы рассчета цифровых фильтров.
Существуют так же прямые методы расчета цифровых фильтров в частотной или временной областях, без аналоговых прототипов.
Последовательности и их представления.
Дискретные сигналы определяются для дискретных значений независимой переменной - времени. Время квантуется обычно равномерно:
T=nT;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.132 (0.01 с.) |







 Отличие их: - физически реализуема.
Отличие их: - физически реализуема.
 Единичный импульс, задержанный на отсчетов.
Единичный импульс, задержанный на отсчетов.














 h(n-m) – отклик системы на
h(n-m) – отклик системы на




















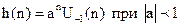

 , то сумма геометрической прогрессии будет равна:
, то сумма геометрической прогрессии будет равна:
 Ее период равен
Ее период равен Достаточно ее знать на интервале
Достаточно ее знать на интервале

 ; - периодическая функция частоты
; - периодическая функция частоты 
 - можно рассматривать как разложение в ряд Фурье, причем коэффициенты разложения являются одновременно отсчетами импульсной характеристики системы. Согласно теории рядов Фурье, коэффициенты h(n) можно выразить:
- можно рассматривать как разложение в ряд Фурье, причем коэффициенты разложения являются одновременно отсчетами импульсной характеристики системы. Согласно теории рядов Фурье, коэффициенты h(n) можно выразить:
 с амплитудами
с амплитудами  .
.



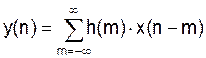
 есть умножение преобразования Фурье от входной последовательности
есть умножение преобразования Фурье от входной последовательности  и частотной характеристики системы
и частотной характеристики системы  – частота дискретизации.
– частота дискретизации.
 с периодом равным
с периодом равным  . Частота
. Частота  - периодична по частоте
- периодична по частоте  . Т.о. частота
. Т.о. частота 
 - периодическая функция частоты f с периодом, равным
- периодическая функция частоты f с периодом, равным  Герц.
Герц. - периодическая функция частоты f с периодом, равным
- периодическая функция частоты f с периодом, равным  Герц.
Герц.
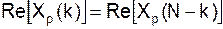

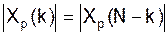
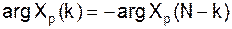

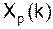 может быть только действительной.
может быть только действительной.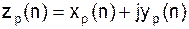
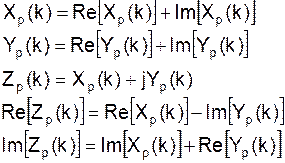
 симметричны, а мнимые – антисимметричны, поэтому получим:
симметричны, а мнимые – антисимметричны, поэтому получим: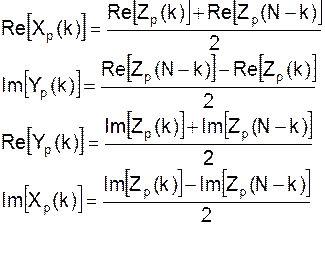
 при
при 
 при других n.
при других n.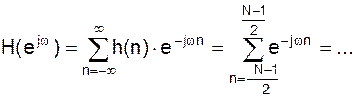


 , где
, где
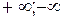 .
. , т.е. никакая конечная задержка не сделает фильтр физически реализуемым.
, т.е. никакая конечная задержка не сделает фильтр физически реализуемым. .
.





 при
при 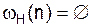 при других n.
при других n.

 - окно Ханна.
- окно Ханна.

 , где
, где  - константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка.
- константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка. - функция Бесселя нулевого порядка.
- функция Бесселя нулевого порядка.






 - ДПФ
- ДПФ - ОДПФ
- ОДПФ - z-преобразование.
- z-преобразование. …
…

 , то:
, то:




 , при
, при 


 (N).
(N).
 ,
,





 ,
,








 ФНЧ с частотой среза в другой ФН с частотой среза а так же
ФНЧ с частотой среза в другой ФН с частотой среза а так же







 - центральная частота полосового фильтра.
- центральная частота полосового фильтра.




