Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурная схема цифровых фильтров.Содержание книги Поиск на нашем сайте
Уравнение цифровой свертки:
Z-преобразование:
где Y(z) – z-преобразование выходной последовательности, X(z) - z-преобразование входной последовательности, H(z) - z-преобразование импульсной характеристики фильтра. Тогда:
Выразим H(z) в виде дробно-рационального полинома от переменной z-1, т.е.:
причем b0 д.б. равно 1. Приведем к общему знаменателю:
Или:
Взяв обратное z-преобразование от левой и правой части (обратное преобразование – не вводилось понятие) можно перейти к последовательностям.
т.к. b0=1, тогда:
Простая форма 1 его реализации:
Запишем:
Обозначив первый и второй множители за H1(z) и H2(z) соответственно, можно получить два фильтра:
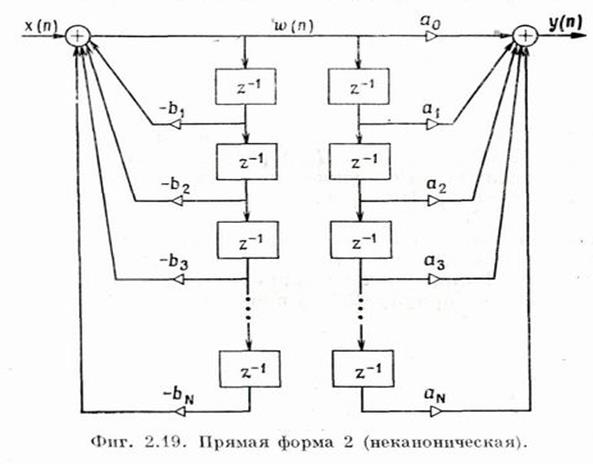
*Прямая форма 2 (неканоническая)
Очевидно, что можно использовать один набор элементов задержки, т.к. задерживается один и тот же сигнал:
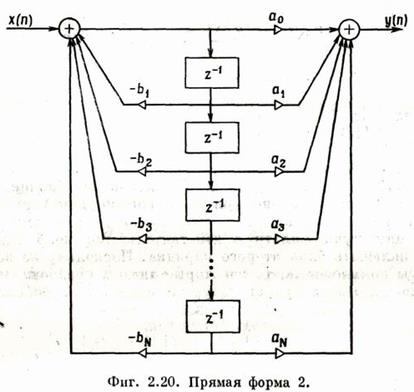
*Прямая форма 2 или каноническая форма Можно записать:
Получим третью структуру построения цифрового фильтра. Множители Hi(z) соответствуют либо блокам второго порядка:
либо блокам первого порядка, т.е.:
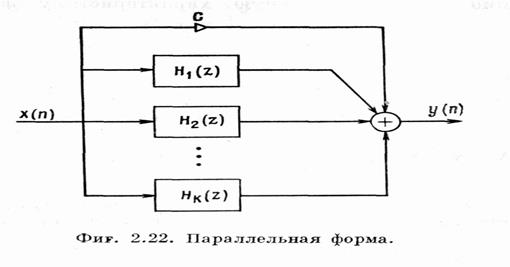
Последовательная (каскадная) форма. Разложим на простые дроби:
где Hi(z) – соответствуют или блокам второго порядка:
или блокам первого порядка:
Структурные схемы фильтров без полюсов В частном случае знаменатель дроби:
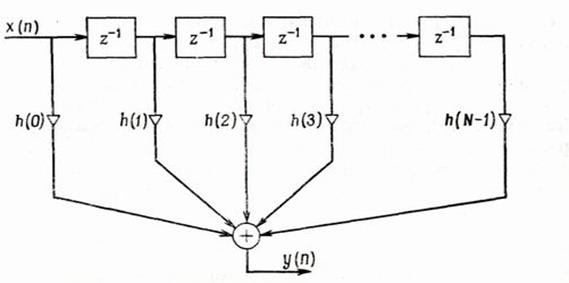
может быть постоянным. Для простоты приравняем его к единице. При этом разностное уравнение становится нерекурсивным, т.е. значение отклика y(n) зависит только от текущего и конечного числа предшествующих значений входной последовательности. В этом случае правую часть преобразуют таким образом, чтобы выразить H(z) непосредственно через импульсную характеристику фильтра:
Разностное уравнение:
т.е. является нерекурсивным уравнением.
Прямая форма фильтра с КИХ.
Дискретное преобразование Фурье Методы описания последовательностей или дискретных систем: - дискретная свертка - преобразование Фурье - z-преобразование.
Когда последовательность периодична или конечна, то ее можно представить рядом Фурье: Рассмотрим последовательность x(n) – периодическую с периодом N отсчетов. Тогда можно представить: (*) причем частоты спектральных составляющих могут принимать значение только:
т.к. периоды других частот не кратны N. В уравнении (*) коэффициенты Xp(k) – амплитуды синусоид с частотами ωр Учитывая избытычность записи (*), т.е.:
можно записать:
т.е. наличие всего N (k=0…n-1) – комплексных синусоид с периодом N-отсчетов. Для удобства можно записать: (**)
Соотношение (**) – носит название обратного дискретного преобразования Фурье (ОДПФ). Можно показать, что коэффициенты (***) Это соотношение (***) называется дискретным преобразованием Фурье (ДПФ). Из (**) и (***) видно, что обе последовательности Ясно также, что Xp(k) полностью определяется одним периодом xp(n). Рассмотрим последовательность конечной длины:
Z-преобразование:
Вычисляя эту сумму при
т.е. учитывая, что xp(n)=x(n) на интервале
Вывод 1: Коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N-точках, равномерно распределенных по единичной окружности. Вывод 2: Коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить саму последовательность, используя обратное ДПФ. Вывод 3: Хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины.
Свойства ДПФ 1. Линейность xp(n) и yp(n) – периодичные последовательности с периодом N каждая. Xp(к) и Yp(к) – их ДПФ. Тогда для последовательности: xp(n)+yp(n) ДПФ будет равно: Xp(к)+Yp(к) Это положение справедливо и для последовательностей конечной длины.
2. Сдвиг xp(n) c периодом N тогда для xp(n-n0) 3. Свойство симметрии Если xp(n) периодическая последовательность в N отсчетов и является действительной, то ее ДПФ удовлетворяет условиям симметрии:
Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-течное ДПФ X(k). Если будет дополнительное условие симметрии:
то окажется, что
Примечание: вычислив одно ДПФ можно получить ДПФ двух последовательностей. xp(n) и yp(n) – действительные последовательности с периодом N отсчетов. Рассмотрим последовательность комплексную:
Ее ДПФ равно:
Действительные части
Если эти две последовательности x(n) и y(n) являются еще и симметричными, то можно сократить еще большее число операций. Нерекурсивные цифровые фильтры.
Порядок расчета фильтров. Свойства КИХ-фильтров. Характеристики КИХ-фильтров с ЛФХ. Частотные характеристики КИХ-фильтров с ЛФХ.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.162.107 (0.011 с.) |

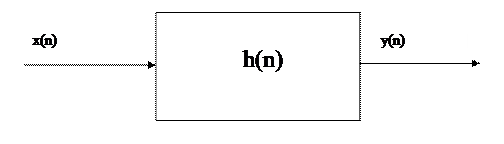
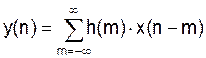
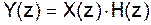
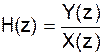

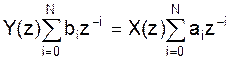

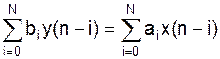
 - уравнение цифрового фильтра.
- уравнение цифрового фильтра.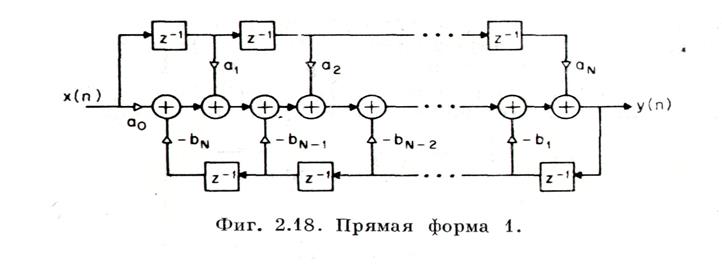
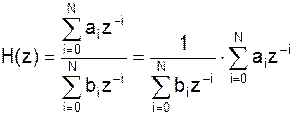
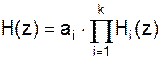
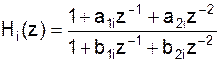
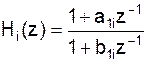

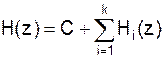
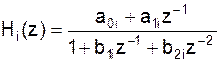
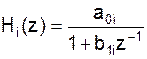
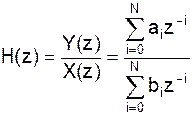

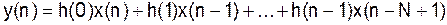
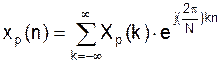
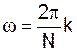 , где
, где 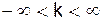
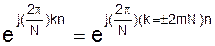 , где 0<n<
, где 0<n< 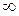
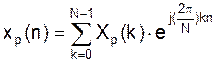 ,
,
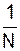 - операция нормировки не изменяет способа представления.
- операция нормировки не изменяет способа представления.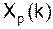 определяются:
определяются:
 и
и 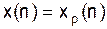 при
при 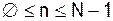
 при других n.
при других n.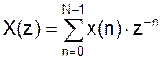
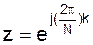 , т.е. в точках на единичной окружности с полярным углом
, т.е. в точках на единичной окружности с полярным углом 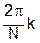 , получим:
, получим: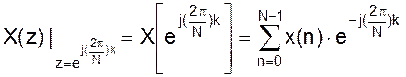 ,
,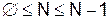 , получим:
, получим:

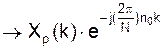
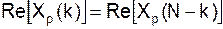

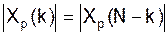
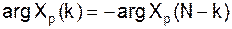

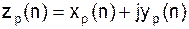
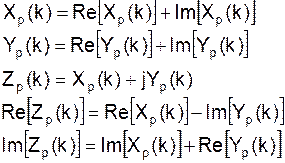
 симметричны, а мнимые – антисимметричны, поэтому получим:
симметричны, а мнимые – антисимметричны, поэтому получим: