
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод отображения дифференциаловСодержание книги Поиск на нашем сайте
Один из наиболее простых методов дискретизации системы – замена дифференциалов в ее дифференциальном управлении на конечные разности, что дает возможность получить разностное уравнение. (**) à (***)
,где x(n) – последовательности на входе ЦФ. y(n) – последовательность на выходе фильтра i-е разности
Причем:
Производная в точках приравнивается (n) или к прямой (справа), или к обратной (слева) разностям.
При использовании обратных разностей:
При использовании обратных разностей:
С точки зрения операторов это соответствует:
при
Действительная и мнимая части z:
Вывод: при использовании обратных разностей устойчивый аналоговый фильтр будет отображаться в устойчивый цифровой фильтр но избирательные свойства аналогового фильтра не будут сохраняться. Прямые разности – можно показать, что ось не отображется в окружность, и что все точки не лежат внутри единичной окружности, т.е. ЦФ получается не всегда устойчивым и его избирательные свойства неизвестны. Поэтому используется метод обобщенных разностей. (Более сложаня методика дискретизации аналоговых фильтров). Первая производная:
где – порядок используемых разностей.
Такое соотношение описывает отображение:
Выбирая значения коэффициентов ai, можно добиться практически любой точности аппроксимации. Однако основная трудность – нахождение этих коэффициентов, поэтому этот метод не нашел практического применения и теоретически не разработан.
Метод инвариантного преобразования импульсной характеристики. Билинейное Z – преобразование. Согласованное Z – преобразование. Обзор методов расчета аналоговых фильтров НЧ (Баттерворта, Бесселя, Чебышева типа 1 и 2, эллиптические фильтры).
Метод инвариантного преобразования импульсной характеристики.
Этот метод также называется методом стандартного преобразования.
В качестве импульсной характеристики рассчитываемого цифрового фильтра используется дискретизированная импульсная характеристика соответствующего аналогового фильтра.
Передаточная характеристика аналогового фильтра:
где
Предположение, что M<N (* - разложение на простые дроби) – является в данном случае обязательным, в противном случае наложения в частотной области станут недопустимыми.
Импульсная характеристика h(t) аналогового фильтра:
Дискретизируя ее получим.
где Т – период дискритизации.
Найдем Z – преобразование.
Изменим порядок суммирования.
Сравним (*) (**), переход от H(s) к H(z) осуществляется с помощью отображения, при котором используется замена:
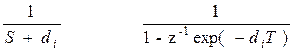
Частотная характеристика цифрового фильтра, рассчитанная методом инвариантного преобразования импульсной характеристики, образуется путем положения частотной характеристики дискретизуемого аналогового фильтра. Т.о.
где
- угловая частота дискретизации цифрового фильтра
Все смежные полосы из S – плоскости будут при отображении накладываться друг на друга в Z – плоскости.
Отсюда следует, что для того что бы частотные характеристики исходного аналогового фильтра и рассчитываемого методом инвариантного преобразования импульсной характеристики цифрового фильтра соответствовали друг другу, необходимо что бы полоса пропускания аналогового фильтра находилась в пределах диапазона.
Для выполнения этого условия необходимо до начала преобразования (т.е. до АЦП) вводить дополнительный фильтр нижних частот, гарантирующий соответствующее ограничение полосы пропускания аналогового фильтра.
Билинейное Z – преобразование.

Вся ось jw перейдет в единичную окружность, левая полуплоскость окажется внутри единичного круга, правая вне его. Учитывая, что:
Можно получить обратную подстановку:
При билинейном преобразовании передаточная функция цифрового фильтра H(z) рассчитывается по формуле.
Из формулы (***) видно, что порядки знаменателей функций H(z) H(s) совпадают, но порядки числителей могут отличаться.
Согласованное Z – преобразование.
Непосредственное отображение полюсов и нулей из S – плоскости в полюсы и нули на Z – плоскости. Полюс (или нуль) в точке s = - a плоскости s отображается в полюс (или нуль) в точке Т.о. имеет место замена:
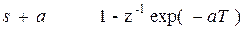
Если полюсы или нули комплексные, тогда:

Обзор методов расчета аналоговых фильтров нижних частот.
Стандартные типы аналоговых фильтров: - Баттерворта - Чебышева 1 типа - Чебышева 2 типа - Кауэра (эллиптические фильтры)
Будем считать, что передаточная функция аналогового фильтра является рациональной функцией переменной S.
Фильтр нормированный с частотой среза, равной Фильтры Баттерворта.
Апроксимация по Баттерворту – фильтры НЧ имеют максимально гладкую амплитудную характеристику в начале координат в S – плоскости. Для частоты среза:
где n – порядок фильтра. Или.
Все полюсы находятся на единичной окружности на одинаковом расстоянии друг от друга в S – плоскости. Можно выразить H(s):
где - а К0 - константа нормирования.
Из формул (*) и (**) – свойства фильтров Баттерворта.
1. Фильтры Баттерворта имеют только полюсы (все нули уходят в бесконечность) 2. На частоте 1 рад/сек, коэффициент передачи фильтров равен:
Т.е. АЧХ спадает на 3 дб (0,707) 3. Порядок фильтра n определяет весь фильтр.
На практике порядок фильтра рассчитывается из условия определения ослабления на некоторой частоте Порядок фильтра определяется по условию уровня АЧХ=1/А на частоте Ω = Ωt по формуле:
Например:
Округлим n в большую сторону до целого числа, получим n=7
Фильтр Чебышева.
Отличительная черта – наименьшая величина максимальной аппроксимации в заданной полосе частот.
Различают поэтому фильтры Чебышева первого и второго типов (максимизируется ошибка аппроксимации в полосе пропускания и в полосе не пропускания)
Фильтры 1 типа.
где Tn (Ω) - полином Чебышева n – го порядка, равный по определению.
а ε - параметр, характеризующий пульсации в полосе пропускания.
Фильтр Чебышева первого порядка имеет только полюса.
Фильтры второго типа.
где Ωr - наименьшая частота, на которой достигается заданный уровень ослабления.
Фильтры второго типа имеют и полюсы и нули.
Фильтры Чебышева 1 и 2 типов определяются любыми из четырех параметров.
1. n – порядок фильтра. 2. ε - параметр, характеризующий пульсации в полосе пропускания. 3. Ωr – наименьшая частота в полосе не пропускания, достигающая заданного ослабления. 4. А – параметр, характеризующий ослабления в полосе пропускания.
Порядок фильтра определяется:
где
Пример:
Получим:
Эллиптические фильтры.
Характеризуются тем, что их амплитудная характеристика имеет равновеликие пульсации в полосе пропускания и в полосе не пропускания. Можно показать, что с точки зрения минимальной ширины переходной полосы эллиптические фильтры являются оптимальными, т.е. для заданных порядка фильтра и уровней пульсации не существует других фильтров с более быстрым переходом от полосы пропускания к полосе не пропускания.
где Rn (Ω,L) - рациональная функция Чебышева. L – параметр, характеризующий пульсации функции Rn (Ω,L)
Переходное отношение:
где Ωp – граничная частота полосы пропускания, а Ωs – граничная частота полосы непропускания. Если ввести параметр K1, равный
то порядок фильтра эллиптического, удовлетворяющего условию заданных значений ε, A, Ωp, Ωs, рассчитывается по формуле:
где K (▪) – полный зллиптический интеграл 1-го рода.
Существуют расчетные диаграммы – по проектированию фильтров нижних частот рассмотренных аппроксимаций (Б,Ч,Э)
Частотные преобразования. Прямые методы расчета цифровых БИХ – фильтров (расчет по квадрату амплитудной характеристики, расчет во временной области). Методы оптимизации при расчете БИХ – фильтров (Минимизация среднеквадратической и Lp – ошибок, оптимизация в W – плоскости с использованием всепропускающих цепей, расчет методом линейного рограммирования).
Частотные преобразования.
Рассмотрим методы расчета ФНЧ непрерывных во времени, а так же методы их дискретизации. При расчете цифровых фильтров ВЧ, ПФ и режекторных, используются два подхода:
1. - Расчет аналогичного ФНЧ - Преобразование полосы частот - Дискретизация фильтра Получаем цифровой фильтр с заданными характеристиками.
2. - Расчет аналогичного ФНЧ - Дискретизация фильтра - Преобразование полосы частот. Получаем цифровой фильтр с заданными характеристиками.
Преобразование полосы частот аналоговых фильтров.
ФНЧ ФНЧ
ФНЧ ФВЧ
ФНЧ ППФ
ФНЧ ПЗФ
где
Преобразование полосы для ЦФ.
В ФВЧ, ППФ и ПЗФ
ФНЧ в ФНЧ
где
ФНЧ в ФВЧ
где
ФНЧ в ППФ
где
ФНЧ в ПЗФ
где
Прямые методы рассчета цифровых фильтров.
Существуют так же прямые методы расчета цифровых фильтров в частотной или временной областях, без аналоговых прототипов.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ;
; и
и  определяются:
определяются:

 - обратная разность;
- обратная разность;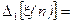
 - прямая разность.
- прямая разность.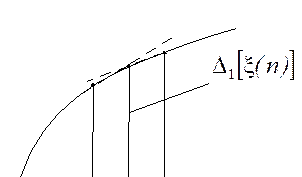

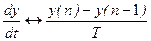
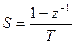 или
или 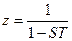
 , получим:
, получим:


 ;
;

 (*) Разложим на простые дроби,
(*) Разложим на простые дроби,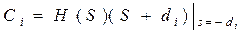

 ,
,
 (**)
(**)
 ,
,
 Каждая горизонтальная полоса, шириной из S – плоскости отображается на Z – плоскость.
Каждая горизонтальная полоса, шириной из S – плоскости отображается на Z – плоскость.

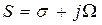

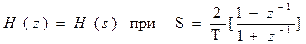 (***)
(***) , где Т – период дискретизации.
, где Т – период дискретизации.
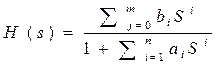
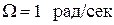
 , (*)
, (*)
 (**)
(**)

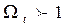 .
.


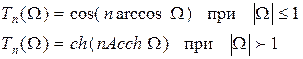

 ,
,





 ,
,








 ФНЧ с частотой среза в другой ФН с частотой среза а так же
ФНЧ с частотой среза в другой ФН с частотой среза а так же







 - центральная частота полосового фильтра.
- центральная частота полосового фильтра.




