
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Где Т – интервал между отсчетамиСодержание книги Поиск на нашем сайте n – целые числа, -5, -4, -3,…, 0, 1, 2, 3,… Обозначения последовательностей:
1. {h(n)},
2. {h(nT)},
3. h(n),
4. h(nT),
1 и 3 – Применяются при неравномерном распределении отсчетов. 2 и 4 – Применяются при равномерном расположении отсчетов.
Способы получения последовательностей.
1)
Взять набор чисел и расположить их в виде последовательности – 0,1,2,3,…,(N-1) Это образует последовательность: 2) Использование рекуррентного соотношения:
h(n)=h(n-1)/2
С начальным условием h(0)=1
Это последовательность:
3) Взять отсчеты равноотстоящие из непрерывного сигнала, т.е. положить.
где Т – интервал дискретизации.
Для получения такой последовательности используется
АЦП – аналого-цифровой преобразователь.
Графические изображения последовательностей:
1 – элемент последовательности, изображающийся отрезком соответствующей длины. 2 – Изображается только огибающая последовательности.
Некоторые важные последовательности.
1)
Цифровой единичный импульс (единичный отсчет)
Его роль такая же, как аналоговый единичный импульс (дельта функция Дирака) в аналоговых системах.
- обобщенная функция или распределение.
2) Единичный скачок:
Единичный скачок выражается через единичный импульс:
3) Убывающая экспонента.
4) Косинусоида
5) Комплексная экспонента
Для ее изображения необходимы раздельные графики вещественной и мнимой части. Можно изобразить в виде вектора, вращающегося с частотой омега.
Многие из этих последовательностей играют важную роль в теории цифровой обработки сигналов.
Представление произвольных последовательностей.
Рассмотрим последовательность а(0), а(1), а(2), …, а(n);
где а(n) – величина n-го элемента.
Такую последовательность можно представить:
Дискретная система.
y(n)=Ф[x(n)]
Линейная система.
x1(n) y1(n)
x2(n) y2(n)
Тогда, если на входе
ax1(n)+bx2(n), а на выходе будет. ay1(n)+by2(n), то система называется линейной.
Система с постоянными параметрами (ЛПП).
x(n) y(n)
x(n-n0) y(n-n0) – при любых n0
где n0 – величина задержки.
Тогда:
Из свойств линейности:
Откликом системы на
Должна быть последовательность
Поэтому отклик на x(n) будет равен:
Заменой переменной можно представить.
Это уравнение представляет собой цифровую свертку. Т.О., чтобы вычислить выходную последовательность системы на заданную входную, необходимо вычислить цифровую свертку входной последовательности и импульсной характеристики системы.
Физическая реализуемость. ЛПП – система физически реализуема, если отклик при n=n0 зависит только от отсчетов входной последовательности с номерами Это означает, что импульсная характеристика h(n) системы равна нулю, при всех
Примеры систем физически нереализуемых. - Идеальный ФНЧ - Идеальный дифференциатор.
Устойчивость ЛПП.
Если при любой ограниченной входной последовательности выходная последовательность так же ограничена.
Необходимое и достаточное условие.
Устойчивость системы:
(*)
Доказательство необходимости.
Пусть (*) не удовлетворяется:
Рассмотрим входную последовательность.
Т.о. последовательность y (0) не ограничена, так, что неравенство (*) является необходимым условием устойчивости. Доказательство достаточности.
Пусть (*) выполняется. На вход поступает ограниченная последовательность Тогда:
Последовательность y(n) ограничена, поэтому система устойчива, что и требовалось доказать.
Примеры импульсных характеристик.
1) Пример устойчивой системы.
2) Пример неустойчивой системы.
Разностные уравнения. В общем виде линейное разностное уравнение М-го порядка с постоянными коэффициентами имеет вид:
Разностные уравнения – это алгоритм функционирования системы. Зная входную последовательность x(m) и начальные условия: x(n-1), x(n-2), …, y(n-1), y(n-2), … Всегда можно определить соответствующую ей выходную последовательность y(n).
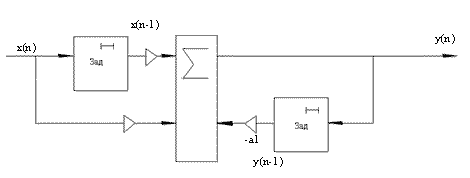
Рассмотрим разностное уравнение первого порядка.
Элемент задержки осуществляет задержку последовательности на один отсчет.
Разностное уравнение второго порядка:
Схема имеет вид:
Частотная характеристика.
При подаче на вход последовательностей вида:
На выходе ЛПП - систем последовательность y(n) будет совпадать с входной, умноженной на некоторый комплексный коэффициент, зависящий только от частоты гармонического сигнала.
Выходная последовательность:
Множитель называется частотной характеристикой ЛПП – систем, т.к. он представляет коэффициент передачи ЛПП – систем для каждого значения частоты.
Пример:
Частотная характеристика:
Т.к.
Свойства частотной характеристики: 1. Частотная характеристика является периодической функцией. 2. 3. 4. Для действительных h(n) (что часто бывает на практике) модуль
5. Поэтому часто частотную характеристику задают на интервале
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |







 Отличие их: - физически реализуема.
Отличие их: - физически реализуема.
 Единичный импульс, задержанный на отсчетов.
Единичный импульс, задержанный на отсчетов.














 h(n-m) – отклик системы на
h(n-m) – отклик системы на




















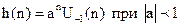

 , то сумма геометрической прогрессии будет равна:
, то сумма геометрической прогрессии будет равна:
 Ее период равен
Ее период равен Достаточно ее знать на интервале
Достаточно ее знать на интервале




