
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок расчета цифрового фильтраСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1. Решение задачи аппроксимации с целью определения коэффициентов фильтра, при которых фильтр удовлетворяет заданным требованиям:
2. Выбор конкретной схемы построения фильтра и квантование значений его коэффициентов в соответствии с фиксированной длиной слова:
3. Квантование переменных величин фильтра, т.е. выбор длины слова входных, выходных и промежуточных переменных (т.е. разрядная сетка входного АЦП, сумматоров и умножителей) 4. Проверка работы фильтра моделированием на ЭВМ, удовлетворяет ли полученный фильтр заданным требованиям. После этапа 4, если требования не удовлетворяются, приходится возвращаться к этапам 2 и 3.
Конечно, желательно бы выполнять три первых этапа одновременно, т.е. решать задачу аппроксимации для произвольной схемы фильтра и для слов произвольной длины, однако маловероятно, что в ближайшем будущем такой подход будет разработан. В настоящее время эта задача не решена.
Свойства КИХ-фильтров.
Основные достоинства этих фильтров: 1) Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой. (Линейная фазовая характеристика особенно важна при обработке речевых сигналов, изображений, а также передаче данных). 2) КИХ-фильтры можно эффективно строить как по рекурсивной, так и по нерекурсивной схемам. 3) КИХ-фильтры, реализуемые нерекурсивно, всегда устойчивые. 4) Нерекурсивные КИХ-фильтрыпозволяют минимизировать шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью (разрядностью).
Недостатки КИХ-фильтры: 1) Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Поэтому при реализации необходимо выполнять большой объем вычислений.
2) Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации.
Характеристики КИХ-фильтров с ЛФХ. Пусть Преобразование Фурье от {h(n)} – частотная характеристика фильтра:
является периодической по частоте с периодом
Рассмотрим действительные последовательности. Тогда (ранее рассматривали), можно получить, что:
т.е. модуль АЧХ – симметричная функция, а ФЧХ – симметричная. На практике часто требуется строго линейная ФЧХ, т.е.:
где
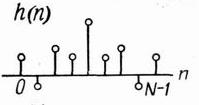
Можно показать, что для этого необходимо, чтобы выполнялись следующие условия: (*) (**) h(n)=h(N-1-n) Уравнение (**) - означает условие симметрии, чтобы ФЧХ была строго линейна. Уравнение (*) – постоянная фазовая задержка. Рассмотрим типичные импульсные характеристики, удовлетворяющие условию симметрии (**) при четно и нечетном N.
Уравнение Если постоянной будет только групповая задержка, можно определить еще один тип фильтра с ЛФХ, т.е.:
тогда условие ЛФХ:
h(n)=h(N-1-n) Рассмотрим типичные импульсные характеристики, удовлетворяющие этим условиям:
Т.о. существуют 4 различных вида КИХ-фильтров с ЛФХ.
Частотные характеристики КИХ-фильтров с ЛФХ. Фильтр вида 1: (симметричная импульсная характеристика, нечетное N) Можно сказать, что ЧХ:
Фильтр вида 2: (симметричная импульсная характеристика, четное N) Можно показать, что ЧХ:
Т.о. отметим, что у таких фильтров:
Фильтр вида 3: (антисимметричная импульсная характеристика, нечетное N)
В том случае ЧХ – ряд синусов:
Фильтр вида 4. (антисимметричная импульсная характеристика, четное N) Частотная характеристика:
Методы расчета КИХ-фильтров c ЛФХ 3 класса методов расчета: 1) Метод взвешивания с помощью окна 2) Методы постоянной выборки 3) Методы расчета оптимальных (по Чебышеву) фильтров
Прямоугольное окно N-точечное прямоугольное окно Весовая функция
Предполагается, что N – четное для простоты. Частотная характеристика – преобразование Фурье:
можно получить:
Метод взве шивания Т.к. частотная характеристика ЦФ – периодическая функция частоты, ее можно представить рядом Фурье:
(*)
Коэффициенты ряда Фурье, т.е. h(n) – совпадает с коэффициентами импульсной характеристики ЦФ.
Трудности использования соотношения (*): 1) Импульсная характеристика h(n) – получается имеет бесконечную длину, т.к. суммирование в пределах 2) Фильтр – физически нереализуем,. Т.к. h(n) начинается в
Один из методов получения КИХ-фильтра, аппроксимирующего заданную функцию Однако простое усечение ряда приводит к хорошо известному явлению Гиббса, которое проявляется в виде выбросов и пульсаций до и после разрывов в аппроксимируемой частотной характеристике и в увеличении переходной полосы. Простое увеличение числа отсчетов h(n), т.е. увеличение M, не всегда приводит к желаемому результату, хотя иногда это приводит к улучшению аппроксимации частотной характеристики. Лучшие результат дает метод, основанный на использовании весовой последовательности конечной длины a(n), называемой окном, для модификации коэффициентов Фурье h(n) в формуле (*) с тем, чтобы управлять сходимостью ряда Фурье.
Вывод: с увеличением N – уменьшается полоса пропускания ФНЧ. Нельзя получить боковой лепесток с подавлением больше чем –13 дБ.
Обобщенное окно Хэмминга Окно имеет вид:
Если Частотная характеристика:
Выводы: 1) Ширина главного лепестка частотной характеристики окна Хэмминга в 2 раза больше, чем для прямоугольного окна. 2) Уровень боковых лепестков в случае окна Хэмминга значительные ниже, чем у характеристики прямоугольного окна. Так при
Окно Кайзера Задача расчета хороших окон практически сводится к математической задаче отыскания ограниченных во времени функций преобразования Фурье которых наилучшим образом аппроксимируют функции, ограниченные по частоте, т.е. имеют минимальную энергию за пределами заданного интервала частот. Для решения этих задач в непрерывном времени был введен класс так называемых вытянутых сфероидальных волновых функций. Эти функции имеют сложный вид. Кайзер – для их аппроксимации ввел окно, которое называется окном Кайзер:
Здесь
Частотная характеристика дискретного окна Кайзера в замкнутом виде не получена.
Окно Кайзера является по существу оптимальным в том смысле, что оно представляет последовательность конечной длины, которая имеет минимум энергии спектра за пределами некоторой заданной частоты.
ФНЧ с различными окнами
Рассмотрим идеальный фильтр нижних частот. Будем использовать 3 окна: - прямоугольное - Хэмминга - Кайзера (в каждом по n=257 отсчетов)
Коэффициенты ряда Фурье:
Частотные характеристики:
Метод частотной выборки (2-й метод)
Метод частотной выборки Это второй метод проектирования КИХ-фильтров. КИХ-фильтр может быть однозначно задан как коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ от импульсной характеристики {H(k)}, т.е.
Они связаны соотношениями: (*) (**) Кроме того:
Тогда можно получить следующее выражение:
меняя порядок суммирования, получим:
Т.к.
Необходимо: 1) Произвести дискретизацию по частоте непрерывной частотной характеристики в N равноотстоящих точках, т.е. взять частотную выборку. Получаемая при этом интерполяционная формула для расчета частотной характеристики фильтра в функции непрерывной частоты имеет вид:
т.е. частотная характеристика фильтра является линейной комбинацией частотных отсчетов интерполирующих функций.
со значениями отсчетов H(k) в качестве коэффициентов.
Недостаток: Необходима дальнейшая оптимизация коэффициентов фильтра для улучшения частотной характеристики.
Метод частотной выборки (2-й метод). Свойства БИХ-фильтров(АЧХ, фазовая характеристика и групповая задержка). Методы расчета коэффициентов БИХ-фильтров. Расчет БИХ-фильтров по аналоговым прототипам. Метод отображения. Свойства БИХ-фильтров. БИХ-фильтры – это цифровые фильтры с бесконечной импульсной характеристикой, при условии, что фильтры являются физически реализуемы:
Форма записи Z-преобразования импульсной характеристики БИХ-фильтров имеет вид: (*) здесь по крайней мере хотя бы один из коэффициентов аi отличен от нуля. Фильтр с передаточной эарактеристикой (*) имеет конечное число нулей (М) и полюсов (N). Нули H(z) могут располагаться на всей z-плоскости, но полюсы H(z) в соответствии с условием устойчивости фильтра обязаны находиться внутри круга единичного радиуса. В большинстве случаев, особенно при расчете цифровых фильтров по характеристикам аналоговых фильтров, (M)
Такие системы (или фильтры) называются системами (или фильтрами) N-го порядка. В отличие от КИХ-фильтров устойчивые, физически реализуемые БИХ-фильтры не обладают строго линейной фазовой характеристикой.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.247 (0.009 с.) |

 - физически реализуемая последовательность конечной длины, заданная на интервале
- физически реализуемая последовательность конечной длины, заданная на интервале  . Это конечная импульсная характеристика (КИХ).
. Это конечная импульсная характеристика (КИХ).
 , т.е.:
, т.е.: , где
, где 
 , при
, при 


 ;
; - постоянная фазовая задержка, выраженная через число интервалов дискретизации.
- постоянная фазовая задержка, выраженная через число интервалов дискретизации.













 при
при  независимо от значений b(n) bkb h(n), т.е. нельзя построить ФВЧ.
независимо от значений b(n) bkb h(n), т.е. нельзя построить ФВЧ.




 .
.


 при
при 
 при других n.
при других n.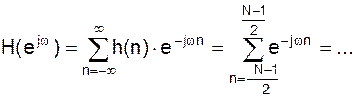


 , где
, где
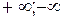 .
. , т.е. никакая конечная задержка не сделает фильтр физически реализуемым.
, т.е. никакая конечная задержка не сделает фильтр физически реализуемым. - усечение (ограничение) бесконечного ряда Фурье (*) за
- усечение (ограничение) бесконечного ряда Фурье (*) за  .
.





 при
при 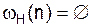 при других n.
при других n.

 - окно Ханна.
- окно Ханна.

 , где
, где  - константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка.
- константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка. - функция Бесселя нулевого порядка.
- функция Бесселя нулевого порядка.






 - ДПФ
- ДПФ - ОДПФ
- ОДПФ - z-преобразование.
- z-преобразование. …
…

 , то:
, то:




 , при
, при 


 (N).
(N).


