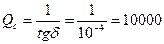Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика расчета вц на четвертьволновых резонаторах (гребенчатый фильтр)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
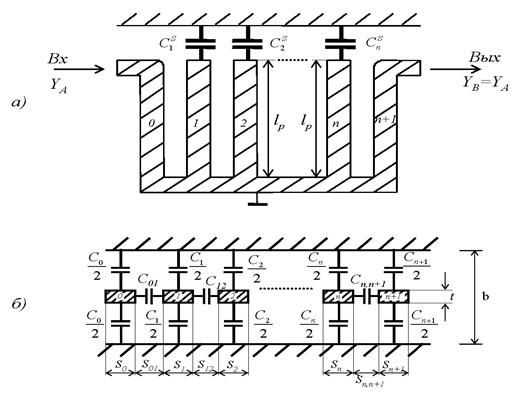
Гребенчатый фильтр применяется в приемнике СВЧ, работающем в длинноволновой части дециметрового диапазона волн для сокращения габаритов фильтра. Гребенчатым называют фильтр, состоящий из решетки параллельно расположенных короткозамкнутых на одном конце отрезков микрополосковой линии, причем все короткозамкнутые концы расположены с одной стороны (рис.2.2). Вид фильтра в плане показан на рис.2.2а, поперечное сечение на рис.2.2б.
Рис. 2.2. Топология (а) и поперечное сечение (б) гребенчатого фильтра.
Короткозамкнутые резонаторы фильтра, длиной порядка Электрические свойства фильтра могут быть охарактеризованы с помощью собственных емкостей на единицу длины каждого стержня относительно земли Сi и взаимных емкостей на единицу длины С i,i+1 между соседними стержнями i и i +1. Выражения для расчета собственных и взаимных емкостей резонаторов фильтра, полученных методом конформных отображений, приведены ниже. Нормированные емкости на единицу длины каждой линии относительно земли рассчитываются по формулам:
Нормированные взаимные емкости между соседними линиями на единицу длины равны:
Сосредоточенные емкости
В выражениях (2.1÷2.3) обозначено:
где
Инверторы проводимости:
где
Параметры элементов связи на входе и выходе:
где ΔF – полоса пропускания фильтра; f0 – средняя частота настройки приемника);
Длина резонатора (полоски) находится по формуле:
Для несимметричной микрополосковой линии вместо
где После определения ширины полоски Si эффективная диэлектрическая проницаемость несимметричной микрополосковой линии уточняется по формуле [8]:
где h - высота подложки. После этого длина полоски (2.7) уточняется. Параметры некоторых материалов подложек приведены в таблице 2.3. Таблица 2.3
Прежде чем приступить к определению конструктивных размеров фильтра, необходимо выполнить рекомендации п.2.1 и произвести расчеты электрических параметров по формулам (2.1÷2.3). Затем выбирают поперечные размеры фильтра Пользуясь рассчитанными взаимными емкостями по формуле (2.2) находят нормированные расстояния Нормированную ширину стержней
где
Для стержней на концах решетки величину Итак, для крайнего левого элемента связи 0 имеем:
Для крайнего правого элемента связи n +1 имеем:
Резонаторы в гребенчатом фильтре состоят из отрезков линий, закороченных на корпус на одном конце и нагруженных на сосредоточенные емкости Линии от i =1 до n являются резонаторами, а линии 0 и n +1 являются элементами связи (петлями связи) на входе и выходе фильтра. Связь между резонаторами осуществляется за счет краевых полей между отрезками линий. После этих расчетов приступают к оформлению топологии и конструкции фильтра.
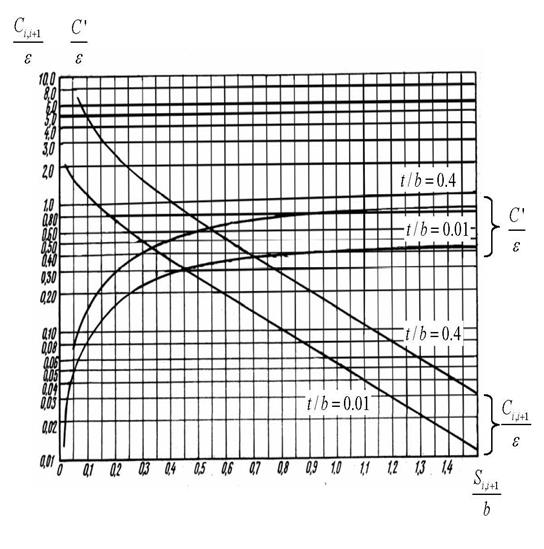
Рис.2.3. Зависимость нормированных взаимной и краевой емкостей от расстояния между стержнями.
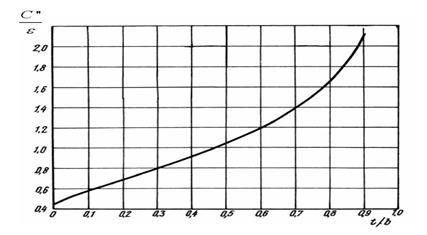
Рис. 2.4.Зависимость нормированной краевой емкости от поперечного размера фильтра.
Далее перейдем к расчету потерь в полосе пропускания, которую можно рассчитать по формуле [3]
где
Считая резонаторы фильтра одинаковыми, можно потери рассчитать по формуле:
где Отсюда
Величину Qc для полосковой линии с медными проводниками можно определить по формуле:
где b - поперечный размер резонатора (рис.2.2б), см; f - частота настройки фильтра, ГГц;
t, Потери в диэлектрике оцениваются по формуле:
где Потери на излучение снижают добротность резонатора, поэтому для несимметричной микрополосковой линии добротность вычисляют по формуле:
где Затухание d в выражении (2.14) берут равным
Рис.2.5.Зависимость α от параметров МПЛ. Пример 2.1. Требуется рассчитать гребенчатый фильтр преселектора приемника СВЧ. Исходные данные: средняя частота настройки приемника АМ сигнала 1. Выберем чебышевскую аппроксимацию характеристики затухания, так как имеют место высокие требования к подавлению зеркального канала. 2. Зеркальный канал приемника расположен на частоте:
Поэтому полоса запирания фильтра равна: 3. В соответствии с заданием полоса пропускания приемника, определяемая фильтрами УПЧ равна П=10МГц, выберем полосу пропускания преселектора 4. Находим отношение: Из графиков рис.1.8 находим, что для подавления зеркального канала, равного L=60дБ, фильтр преселектора должен состоять из n =4 звеньев (резонаторов) при пульсациях на вершине характеристики Если преселектор приемника состоит из входной цепи и УВЧ целесообразно заданную избирательность по зеркальному каналу поделить поровну между входной цепью и УВЧ, т.е. по 30 дБ. Тогда по тем же графикам находим, что фильтр СВЧ должен быть более чем второго класса. Берем n=3. 5. Рассчитаем электрические характеристики фильтра при n=3. Согласно заданию: Электрическую длину резонатора берем Волновое сопротивление резонаторов фильтра берем
Выберем в качестве материала подложки - поликор с
Параметры прототипа находим из таблицы 2.2. g0=1; g1=2,02; g2=0,99; g3=2,02; g4=1. Из выражения (2.4) получаем
Из формулы (2.6) находим промежуточные параметры:
Находим нормированные емкости на единицу длины линии по формулам (2.1):
Находим нормированные взаимные емкости между линиями по формулам (2.2):
Сосредоточенные емкости на концах линий находим по формуле (2.3):
6. Задаемся поперечным размером фильтра b=10мм и Расстояние Si,i+1 между полосками фильтра находим из графика рис.2.3 и рассчитанным взаимным емкостям
Ширину полосок рассчитываем по формулам 2.10
Уточненное значение эффективной диэлектрической проницаемости по формуле (2.9) дает
7. Рассчитаем потери фильтра в полосе пропускания. Расчет по формуле (2.14) производим в следующем порядке. Определяем потери в проводниках:
Потери в диэлектрике находим по формуле:
Расчет потерь по формуле (2.14) дает:
8. Эскиз фильтра показан на рис. 2.6.
Рис. 2.6. Эскиз гребенчатого фильтра.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.01 с.) |

 , обозначены номерами от 1 до n. Номерами 0 и n +1 обозначены элементы связи (петля связи) на входе и выходе фильтра.
, обозначены номерами от 1 до n. Номерами 0 и n +1 обозначены элементы связи (петля связи) на входе и выходе фильтра.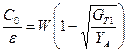


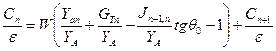
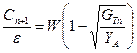
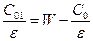
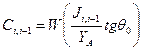
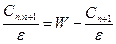
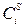 равны:
равны: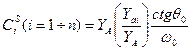
 ,
,
 - волновое сопротивление элемента связи на входе фильтра,
- волновое сопротивление элемента связи на входе фильтра,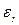 - относительная диэлектрическая проницаемость среды фильтра,
- относительная диэлектрическая проницаемость среды фильтра, - абсолютная диэлектрическая проницаемость.
- абсолютная диэлектрическая проницаемость. ,
,
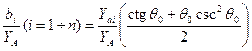
 ,
,  Ом, 75Ом);
Ом, 75Ом);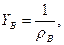
 - волновое сопротивление выходного тракта (обычно
- волновое сопротивление выходного тракта (обычно 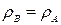 );
);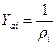 ,
,  - волновое сопротивление i -го резонатора фильтра (
- волновое сопротивление i -го резонатора фильтра ( Ом
Ом 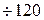 Ом);
Ом); - электрическая длина резонатора (для резонаторов укороченных емкостью
- электрическая длина резонатора (для резонаторов укороченных емкостью 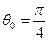 );
); , где
, где  [м] - длина волны в свободном пространстве.
[м] - длина волны в свободном пространстве. ;
;  ,
,
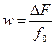 - относительная полоса;
- относительная полоса;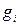 - параметры прототипа (таблицы 2.1,2.2).
- параметры прототипа (таблицы 2.1,2.2).
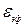 :
: ,
,
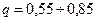 [3]
[3]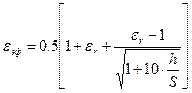 ,
,


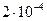

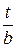 (рис.2.2б) (для МПЛ можно взять
(рис.2.2б) (для МПЛ можно взять  ).
). между стержнями (полосками) фильтра по графику рис.2.3
между стержнями (полосками) фильтра по графику рис.2.3 рассчитывают по формуле:
рассчитывают по формуле: ,
,
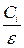 - нормированные емкости каждой линии (стержня) относительно земли, вычисленные по формуле (2.1);
- нормированные емкости каждой линии (стержня) относительно земли, вычисленные по формуле (2.1);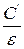 - нормированные краевые емкости, определяют из графиков рис.2.3 по зазорам
- нормированные краевые емкости, определяют из графиков рис.2.3 по зазорам  для левого и
для левого и  для правого стержня необходимо заменить величиной
для правого стержня необходимо заменить величиной  , которая находится из графика рис.2.4.
, которая находится из графика рис.2.4.
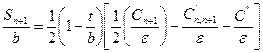
 ,
,
 - затухание в i -ой линии (Qi -добротность i -ой линии).
- затухание в i -ой линии (Qi -добротность i -ой линии).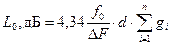 ,
,
 (добротность Q МПЛ определяется потерями в проводниках Qc и потерями в диэлектрике Qd, то есть:
(добротность Q МПЛ определяется потерями в проводниках Qc и потерями в диэлектрике Qd, то есть: 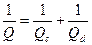 ).
).
 ,
,
 - находится из графика рис.2.5 [6];
- находится из графика рис.2.5 [6]; - толщина полоски и волновое сопротивление соответственно.
- толщина полоски и волновое сопротивление соответственно. ,
,
 находится из таблицы 2.3.
находится из таблицы 2.3.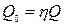 ,
,
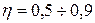 .
.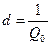

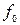 =1,2 ГГц; полоса пропускания приемника П=10 МГц; промежуточная частота
=1,2 ГГц; полоса пропускания приемника П=10 МГц; промежуточная частота 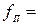 60 МГц; ослабление зеркального канала приемника
60 МГц; ослабление зеркального канала приемника  60 дБ. На входе и выходе фильтр должен быть согласован с трактом с волновым сопротивлением
60 дБ. На входе и выходе фильтр должен быть согласован с трактом с волновым сопротивлением  Ом. Габариты фильтра должны быть минимальны.
Ом. Габариты фильтра должны быть минимальны.
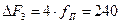 МГц.
МГц. в несколько раз больше т.е.:
в несколько раз больше т.е.: 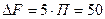 МГц
МГц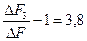
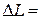 1дБ.
1дБ. Ом;
Ом; 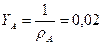 ;
; 
 Ом
Ом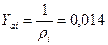

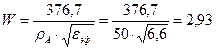



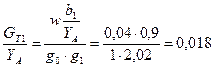


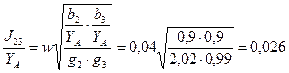
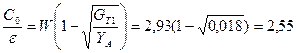







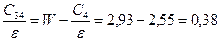
 пФ
пФ
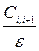 :
: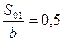 ,
,  ,
, 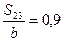 ,
,  ;
; мм,
мм,  мм,
мм, 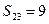 мм,
мм,  мм.
мм. 2.12:
2.12: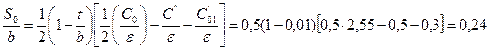
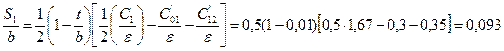



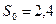 мм;
мм;  мм;
мм;  мм;
мм;  мм;
мм; 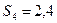 мм.
мм. Длину резонаторов находим по формуле (2.7):
Длину резонаторов находим по формуле (2.7):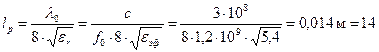 мм
мм