Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Принципы расчета строительных конструкций по методу предельных состоянийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 2. Принципы расчета строительных конструкций по методу предельных состояний Понятие о предельных состояниях конструкций; расчетные ситуации. Классы ответственности зданий, категории конструкций и их элементов. Расчет конструкций по первой группе предельных состояний. Расчет конструкций по второй группе состояний. Нормативные и расчетные сопротивления. Выбор марок сталей для строительных конструкций. Понятие о предельных состояниях конструкций; расчетные ситуации. В настоящее время все строительные конструкции рассчитываются по методу предельных состояний [1]. В основе метода лежит понятие о предельных состояниях конструкций. Под предельными состояниями подразумеваются такие состояния, при которых конструкции перестают удовлетворять предъявляемым к ним в процессе эксплуатации или при возведении требованиям, заданным в соответствии с назначением и ответственностью сооружений. Различают две группы предельных состояний. Предельные состояния первой группы характеризуются потерей несущей способности и полной непригодностью конструкций к эксплуатации. К предельным состояниям первой группы относятся: ü разрушение любого характера (вязкое, хрупкое, усталостное); ü общая потеря устойчивости формы; ü потеря устойчивости положения; ü переход конструкции в изменяемую систему; ü качественное изменение конфигурации; ü развитие пластических деформаций, чрезмерных сдвигов в соединениях и т. д. Выход за границы первой группы предельных состояний означает полную утрату работоспособности конструкции. Предельные состояния второй группы характеризуются непригодностью к нормальной эксплуатации, вследствие появления: ü чрезмерных перемещений (прогибов, углов поворота); ü недопустимых колебаний (чрезмерных амплитуд, частот, ускорений); ü трещин или чрезмерного раскрытия их в железобетонных конструкциях. В соответствии с действующими нормами [1] при расчете строительных конструкций следует рассматривать такие типы расчетных ситуаций: ü установившаяся расчетная ситуация, продолжительность реализации которой Tsit того же порядка, что и срок эксплуатации конструкции Tef. (например, период эксплуатации между капитальными ремонтами); ü переходная расчетная ситуация, продолжительность реализации которой Tsit невелика по сравнению со сроком эксплуатации конструкции Tef., т.е. Tsit ‹ Tef. (например, период капитального ремонта); ü аварийная расчетная ситуация, продолжительность реализации которой Tsit незначительна по сравнению со сроком эксплуатации конструкции Tef., т.е. Tsit ‹‹ Tef., но последствия ее реализации могут быть достаточно важными с точки зрения возможных отказов (например, взрыв, землетрясение, авария оборудования). Срок эксплуатации Tef. определяется при проектировании и согласовывается заказчиком. Допускается принимать срок эксплуатации в соответствии с данными табл. 2.1 Таблица 2.1. – Ориентировочные сроки эксплуатации зданий и сооружений Tef
Нормативные и расчетные сопротивления стали
В металлических конструкциях различают два вида расчетного сопротивления R: Ry – расчетное сопротивление, установленное по пределу текучести и используемое в расчетах, предполагающих упругую работу материала; Ru – расчетное сопротивление, установленное по пределу прочности и используемое в расчетах конструкций, где допустимы значительные пластические деформации. Расчетное сопротивление Ry и Ru определяются соответственно по формулам: Ry = Ryn/gm, Ru = Run/gm, где Ryn и Run – нормативные сопротивления, соответственно равные: Ryn = sm, Run = sв. В приведенных формулах sm – предел текучести, sв – предел прочности (временного сопротивления) материала; gm – коэффициент надежности по материалу, учитывающий изменчивость свойств материала и выборочный характер испытаний образцов по определению sm и sв. Этот коэффициент учитывает также масштабный фактор – механические характеристики определяются на малых образцах при кратковременном одноосном растяжении, в то время как металл работает длительное время в большеразмерных конструкциях. Значение нормативных сопротивлений Ryn = sm и Run = sв, а также значения коэффициента gm устанавливают статистически. Нормативные сопротивления имеют статистическую обеспеченность не менее 0,988. Это означает, что в 988 случаях из 1000, значения предела текучести sm и предела прочности sв, будут не менее значений, указанных в сертификате на сталь. Коэффициент надежности по материалу gm устанавливается на основании анализа кривых распределения, полученных в результате испытаний образцов стали. Значения этого коэффициента в зависимости от государственного стандарта или технических условий на сталь дает табл. 1.3.2 ДБН [4]. Значения коэффициента gm изменяются от 1,025 до 1,050. Нормативные Ryn и Run и расчетные Ry и Ru сопротивления для разных марок стали в зависимости от вида проката (лист или фасон) и его толщины представлены в табл.Е.2 ДБН [2]. В расчетах также используют расчетное сопротивление на сдвиг (срез) Rs =0,58 Ry, на смятие Rp = Ru и др. Нормативные и расчетные сопротивления для некоторых наиболее применяемых марок сталей приведены в табл. 2.5. Таблица 2.5 -- Нормативные и расчетные сопротивления стали по ГОСТ 27772-88.
Таким образом, в методе предельных состояний все исходные величины, случайные по своей природе, представляются в нормах некоторыми нормативными значениями, а влияние их изменчивости на конструкцию учитывается соответствующими коэффициентами надежности. Каждый из введенных коэффициентов учитывает изменчивость лишь одной исходной величины (нагрузки, условий работы, свойств материалов, степени ответственности сооружения). Эти коэффициенты часто называют частными, а сам метод расчета по предельным состояниям за рубежом называют методом частных коэффициентов. Тесты для самоконтроля 1. Потеря устойчивости относится к предельным состояниям: А – I группы; Б – II группы; В – III группы. 2. Коэффициент γm учитывает: А – условия работы конструкции; Б – изменчивость свойств материала; В – изменчивость нагрузок.
3. Расчетное сопротивление Ry определяют по формуле: А – Ry = Ryn / γm ; Б – Ry = Run / γn ; В – Ry = Run / γc. 4. Непригодность конструкций к эксплуатации характеризует предельное состояние: А – I группы; Б – II группы; В – III группы. 5. Коэффициент γn учитывает: А – степень ответственности сооружения; Б – изменчивость свойств материала; В – изменчивость нагрузок. 6. Расчетное сопротивление Ry устанавливают: А – по пределу упругости; Б – по пределу текучести; В – по пределу прочности. 7. Коэффициент γfm применяют для определения расчетной нагрузки: А – предельной; Б – эксплуатационной В – циклической. 8. Расчет на устойчивость выполняют с учетом расчетной нагрузки: А – предельной; Б – эксплуатационной; В – циклической. 9. Хрупкое разрушение относится к предельным состояниям: А – I группы; Б – II группы; В – III группы. 10. Здания высокой степени ответственности относятся к группе: А – СС3; Б – СС2; В – СС1. 11. Расчетное сопротивление Rи определяют по формуле: А – Rи = Rиn / γm; Б – Rи = Run / γn; В – Rи = Run / γc. 12. Коэффициент γс учитывает: А – степень ответственности сооружения; Б – изменчивость свойств материала; В – условия работы конструкции. 13. Проверка трещиностойкости железобетонной конструкции относится: А – к I группе предельных состояний; Б – ко II группе предельных состояний; В – к III группе предельных состояний.
Тема 2 (продолжение) Классификация нагрузок. Нагрузка от веса конструкций и грунта. Нагрузки на перекрытия и покрытия зданий. Снеговая нагрузка. Ветровая нагрузка. Сочетания нагрузок.
Классификация нагрузок
Нагрузки и воздействия подразделяются на механические и немеханической природы, приводящие к снижению несущей способности и эксплуатационной пригодности конструкций Механические нагрузки (силы, приложенные к конструкции, или вынужденные деформации) учитываются в расчетах непосредственно. Воздействия немеханической природы, например, влияние агрессивной среды, как правило, в расчете учитывается косвенно. В зависимости от причин возникновения нагрузки и воздействия подразделяются на основные и эпизодические. В зависимости от изменчивости во времени нагрузки и воздействия подразделяются на постоянные и переменные (временные). Переменные (временные) нагрузки делятся на: длительные; кратковременные; эпизодические. Основой для назначения нагрузок являются их характеристические значения. Расчетные значения нагрузок определяются умножением характеристических значений на коэффициент надежности по нагрузке, зависящий от вида нагружения. В зависимости от характера нагрузок и целей расчета используют четыре вида расчетных значений – предельное; эксплуатационное; циклическое; квазипостоянное. Их значения определяют соответственно по формулам: Fm = F0 · γf m · γ n, (2.5) Fe = F0 · γf e · γ n, (2.6) Fc = F0 · γf c · γ n, (2.7) Fp = F0 · γf p · γ n (2.8) где F0 – характеристические значения нагрузок; γfm, γfe, γfc, γfp – коэффициенты надежности по соответствующим нагрузкам; γ n – коэффициенты надежности по назначению сооружения, учитывающие степень его ответственности (см. табл. 2.2). К постоянным нагрузкам относят: ü вес несущих и ограждающих конструкций здания; ü вес и давление грунтов (насыпей, засыпок); ü усилие от предварительного напряжения в конструкциях. К переменным длительным нагрузкам относят: ü вес временных перегородок, подливок, подбетонок под оборудование; ü вес стационарного оборудования и его заполнения жидкостями, сыпучими телами; ü давление газов, жидкостей и сыпучих тел в ёмкостях и трубопроводах; ü нагрузки на перекрытия от складируемых материалов в складах, архивах; ü температурные технологические воздействия от оборудования; ü вес слоя воды в водонаполненных покрытиях; ü вес отложения производственной пыли; ü воздействия, обусловленные деформациями основания без изменения структуры грунта; ü воздействия, обусловленные изменением влажности, агрессивности среды, усадкой и ползучестью материалов. К переменным кратковременным нагрузкам относят: ü снеговые нагрузки; ü ветровые нагрузки; ü гололедные нагрузки; ü нагрузки от подвижного подъемно-транспортного оборудования, включая мостовые и подвесные краны; ü температурные климатические воздействия; ü нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и сельскохозяйственных зданий; ü вес людей, ремонтных материалов в зоне обслуживания оборудования; ü нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах. К эпизодическим нагрузкам относят: ü сейсмические воздействия; ü взрывные воздействия; ü нагрузки аварийные, вызванные нарушениями технологического процесса, поломкой оборудования; ü нагрузки, обусловленные деформациями основания с коренным изменением структуры грунта (при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых районах. Характеристические и расчетные значения эпизодических нагрузок определяются специальными нормативными документами.
Снеговая нагрузка Снеговая нагрузка является переменной, для которой установлены три расчетных значения: предельное, эксплуатационное и квазипостоянное. Для расчета без учета реологических свойств материала используют предельное и эксплуатационное расчетные значения снеговой нагрузки. Предельное расчетное значение снеговой нагрузки на горизонтальную проекцию покрытия определяется по формуле: Sm = S0 · C · γfm (2.9) где S0 – характеристическое значение снеговой нагрузки, равное весу снегового
покрова на 1м2 поверхности земли. Значения S0 определяются в зависимости от снегового района по карте районирования или по приложению Е [2]. На территории Украины выделено шесть снеговых районов. Максимальные характеристические значения нагрузки для каждого из шести снеговых районов приведены в табл. 2.10. Город Запорожье расположен в III снеговом районе. Таблица 2.10 – Максимальные значения характеристической снеговой нагрузки
Более точные характеристические значения снеговой и ветровой нагрузок для некоторых городов Украины приведены в табл. 2.11. Коэффициент С в формуле (2.9) определяется по формуле: С = μ · Се · Саlt, где: Се – коэффициент учитывающий режим эксплуатации кровли; Саlt – коэффициент географической высоты; μ – коэффициент перехода от веса снегового покрова на поверхности земли к снеговой нагрузке на покрытии, зависящий от формы кровли. Для зданий с односкатными и двухскатными покрытиями (рис. 2.1) значения коэффициента μ принимают равным: μ = 1 при α ≤ 250, μ = 0 при α > 600, где α – угол наклона кровли. Промежуточные значения μ определяются линейной интерполяцией Варианты 2 и 3 следует учитывать для зданий с двухскатными профилями (профиль б), при этом вариант 2 – 20 0 ≤ α ≤ 300, а вариант 3 – 100 ≤ α ≤ 300 только при наличии ходовых мостиков или аэрационных устройств.
с покрытиями других очертаний можно найти в приложении Ж [2]. Коэффициент Се в формуле (2.9), учитывает влияние режима эксплуатации на накопление снега на кровле (очистку, таяние и др.), устанавливается заданием на проектирование. Для неутепленных покрытий цехов с повышенным тепловыделением при уклонах кровли свыше 3% и обеспечении надлежащего отвода талой воды следует принимать Се =0,8. При отсутствии данных о режиме эксплуатации кровли допускается принимать Се = 1. Коэффициент Саlt – учитывает географическую высоту Н (км) размещения строительного объекта над уровнем моря. При Н < 0,5 км, Саlt = 1, при Н ≥ 0,5 км значение Саlt можно определить по формуле: Саlt = 1,4Н + 0,3 Таблица 2.11 – Характеристические значения ветровых и снеговых нагрузок для некоторых городов Украин
Коэффициент надежности по предельному расчетному значению снеговой нагрузки γfm в формуле (2.9) определяется в зависимости от заданного среднего периода повторяемости Т по табл. 2.12 Таблица 2.12 – Коэффициент γfm по предельному значению снеговой нагрузки
Промежуточные значения γfm следует определять линейной интерполяцией Для объектов массового строительства допускается период повторяемости аварийной ситуации Т принимать равным установленному сроку эксплуатации конструкции Теf (см. табл.2.1). Эксплуатационное расчетное значение снеговой нагрузки определяется по формуле: Se = So · C · γfe, (2.10) где So и C – то же что и в формуле (2.9); γfe – коэффициент надежности по эксплуатационному значению снеговой нагрузки, определяемый по таблице 2.11 в зависимости от доли времени η на протяжении которой могут нарушаться условия второго предельного состояния; промежуточное значение γfe следует определять линейной интерполяцией. Таблица 2.13. Коэффициент γfe по эксплуатационному значению снеговой нагрузки
Значение η принимается по нормам проектирования конструкций или устанавливается заданием на проектирование в зависимости от их назначения, ответственности и следствий выхода за предельное состояние. Для объектов массового строительства допускается принимать η = 0,02 (2% времени от срока службы сооружения).
Ветровая нагрузка Ветровая нагрузка является переменной, для которой установлены два расчетных значения: предельное и эксплуатационное. Предельное расчетное значение ветровой нагрузки определяется по формуле: wm = w0 · C γfm, (2.11) где С – коэффициент определяемый по формуле (2.12); γfm – коэффициент надежности по предельному значению ветровой нагрузки; w0 - характеристическое значение ветровой нагрузки, равное средней (статической) составляющей давления ветра на высоте 10м над поверхностью земли. Значение w0 определяется в зависимости от ветрового района по карте районирования или по приложению Е [5]. На территории Украины выделено пять ветровых районов. Максимальные характеристические значения нагрузки для каждого из ветровых районов приведены в табл. 2.14. Город Запорожье расположен в III ветровом районе.
Таблица 2.14 – Максимальные характеристические значения ветровой нагрузки
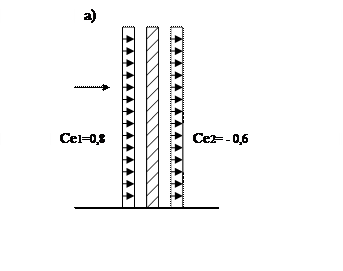
Более точные значения характеристической ветровой нагрузки для некоторых городов Украины приведены в табл. 2.11 Коэффициент С в формуле (2.11) определяется по формуле: С = Саер · Сh · Calt ·Crel · Cdir · Cd (2.12) где Саер – аэродинамический коэффициент; Сh - коэффициент высоты сооружения; Calt – коэффициент, учитывающий географическую высоты местности; Crel – коэффициент, учитывающий рельеф местности; Cdir – коэффициент направления; Cd – коэффициент динамичности. Современные нормы предусматривают несколько аэродинамических коэффициентов: – внешнего воздействия Се; – трения Сf; – внутреннего воздействия Ci; – лобового сопротивления Сх; – поперечной силы Су. Значения аэродинамических коэффициентов определяются по приложению И [5] в зависимости от формы сооружения или конструктивного элемента. При расчете рам каркасов зданий обычно используют аэродинамический коэффициент внешнего воздействия Се. На рисунке 2.2 представлены сооружения простейшей формы, схемы ветрового давления на поверхности и аэродинамические коэффициенты внешнего воздействия к ним.
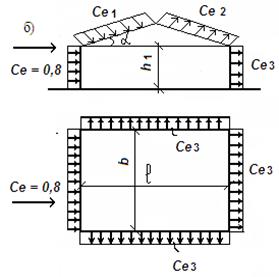
а – отдельно стоящие плоские сплошные конструкции; б – здания с двускатными покрытиями. Рис.2.2. Схемы ветровых нагрузок Для зданий с двускатными покрытиями (рис.3.2,б) аэродинамический коэффициент активного давления Се = + 0,8; значения коэффициентов Се1 и Се2 в зависимости от размеров здания приведены в табл. 2.15, коэффициент Се3 – в табл.2.16. Таблица 2.15 – Значения коэффициентов Се1 и Се2
Таблица 2.16 – Значения коэффициентов Се3
Знак «плюс» у коэффициентов соответствует направлению давления ветра на поверхность, знак «минус» - от поверхности. Промежуточные значения коэффициентов следует определять линейной интерполяцией. Максимальное значение коэффициента для откоса Се3 = 0,6. Коэффициент высоты сооружения Сh учитывает увеличение ветровой нагрузки по высоте здания и зависит от типа окружающей местности. Для одноэтажных зданий коэффициент Сh определяется по табл. 2.17. Таблица 2.17. -- Значения коэффициентов Сh для одноэтажных зданий
Для многоэтажных зданий, у которых период собственных колебаний первой формы Т1 > 0,25 сек, значения коэффициента Сh определяется по табл.2.18. Таблица 2.18. -- Значения коэффициентов Сh для многоэтажных зданий, у которых первый период собственных колебаний Т1 >0,25с
Типы местности, окружающей сооружение, определяются для каждого расчетного направления ветра в отдельности: I – открытые поверхности морей, озер, а также равнины без препятствий, подвергающееся действию ветра на участке длиной не менее 3 км; II – сельская местность с оградами (заборами), небольшими сооружениями, домами и деревьями; III – пригородные и промышленные зоны, протяженные лесные массивы; IV – городские территории, на которых по крайней мере 15% поверхности занято зданиями, имеющими среднюю высоту более 15 м. Сооружение считается расположенным на местности данного типа для определенного расчетного направления ветра, если в рассматриваемом направлении такая местность располагается на расстоянии 30 Z при полной высоте сооружения Z < 60м или 2 кмпри Z > 60м (Z – высота здания). Коэффициент географической высоты Calt учитывает высоту Н (км) размещения строительного объекта над уровнем моря и определяется по формулам: Calt = 2Н, при Н > 0,5 км, Calt = 1, при Н ≤ 0,5 км. Коэффициент рельефа Crel учитывает микрорельеф местности вблизи площадки, на которой расположен строительный объект. Crel = 1 за исключением случаев, когда объект строительства расположен на холме или на склоне. Коэффициент направления Cdir учитывает неравномерность ветровой нагрузки по направлению ветра и, как правило, принимается Cdir = 1. Значения коэффициента Cdir ≠ 1 принимается при специальном обосновании только для открытой равнинной местности. Коэффициент динамичности Cd учитывает, влияние пульсационной составляющей ветровой нагрузки и пространственную корреляцию ветрового давления на сооружение. Для одноэтажных зданий Cd = 1. Для многоэтажных зданий, у которых первый период собственных колебаний Т1 >0,25сек, значения коэффициента Cd определяются по графикам на рис 9.5 (для каменных зданий и зданий с железобетонным каркасом) и 9.6 (для зданий со стальным каркасом) [3] Коэффициент надежности по предельному расчетному значению ветровой нагрузки γfm определяется в зависимости от заданного среднего периода повторяемости Т по таблице 2.19.
Таблица 2.19. -Коэффициент надежности по предельному расчетному значению ветровой нагрузки γfm
Промежуточные значения γfm следует определять линейной интерполяцией. Для объектов массового строительства допускается средний период повторяемости Т принимать равным установленному сроку эксплуатации конструкции Тef (см. табл. 2.1). Эксплуатационное расчетное значение ветровой нагрузки определяется по формуле: wе = w0 · C γfе ,, (2.13)
где w0 и C – то же, что и в формуле (2.12); γfe – коэффициент надежности по эксплуатационному расчетному значению ветровой нагрузки, определяемый по таблице 2.20 в зависимости от доли времени η на протяжении которой могут нарушаться условия второго предельного состояния. Промежуточное значение γfe следует определять линейной интерполяцией. Значение η принимается по нормам проектирования конструкций или устанавливается заданием на проектирование в зависимости от их назначения, ответственности и последствий выхода за предельное состояние. Для объектов массового строительства η = 0, 02.
Таблица 2.20 – Коэффициент надежности по эксплуатационному расчетному значению ветровой нагрузки γfe
Сочетания нагрузок
В расчетах конструкций могут использоваться сочетания двух типов: ü основные; ü аварийные. Для проверки предельных состояний I группы используются основные сочетания, включающие постоянные нагрузки с предельными расчетными значениями, а также предельные расчетные, циклические или квазипостоянные значения переменных нагрузок. Для проверки предельных состояний II группы используются основные сочетания с эксплуатационными расчетными значениями постоянных, циклических или квазипостоянные нагрузок. В аварийно е сочетание кроме постоянных и переменных нагрузок может входить только одно эпизодическое воздействие (например, сейсмика или взрыв). Основны е сочетания включают в себя постоянную и переменные нагрузки. Малая вероятность одновременной реализации расчетных значений нескольких нагрузок учитывается умножением расчетных значений нагрузок, вошедших в сочетание, на коэффициент сочетания ψ Основные сочетания включают в себя постоянную нагрузку, одну или несколько переменных (длительных или кратковременных), причем длительные нагрузки учитываются с коэффициентом сочетания ψ1 = 0,95, а кратковременные с коэффициентом ψ2 = 0,9. Если учитывается только одна переменная нагрузка (длительная или кратковременная), то ее нужно взять с коэффициентом сочетания ψ = 1. Аварийное сочетаниевключает в себя постоянную нагрузку и не менее двух переменных (длительных или кратковременных), причем длительные нагрузки учитываются с коэффициентом ψ1 = 0,95, а кратковременные с коэффициентом ψ2 = 0,8 и одну эпизодическую с коэффициентом ψ3 = 1. В сочетания должны входить нагрузки, которые наиболее неблагоприятно влияют на конструкции. Взаимоисключающие воздействия не могут входить в одно сочетание.
Тесты для самоконтроля 1. Предельное расчетное значение нагрузки определяют по формуле: А – Fm = F0 · γf m · γ n, Б – Fe = F0 · γf e · γ n, В – Fp = F0 · γf p · γ n, 2. Коэффициент Сh при подсчете ветровой нагрузки зависит от: А – района строительства; Б – типа местности; В – географической высоты. 3. Если уклон кровли α=450, то значение коэффициента μ для определения снеговой нагрузки: А – μ=0; Б – μ=1; В – определяется линией интерполяцией 4.. К переменным длительным относятся нагрузки: А – от собственного веса конструкций; Б – от собственного веса оборудования; В – от снега. 5. Максимальное значение для аэродинамического коэффициента для ветрового отсоса: А – се3= -1; Б – се3= -0,8; В – се3= -0,6. 6. Максимальное значение для аэродинамического коэффициента для активного ветрового давления: А – се3=1; Б – се3=0,8; В – се3=0,6. 7. Характеристическое значение ветровой нагрузки W0 зависит от: А – района строительства; Б – типа местности; В – высоты местности. 8. Нагрузка от людей на перекрытие является: А – кратковременной; Б – длительной; В – постоянной. 9. К постоянным относятся нагрузки: А
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.149 (0.015 с.) |

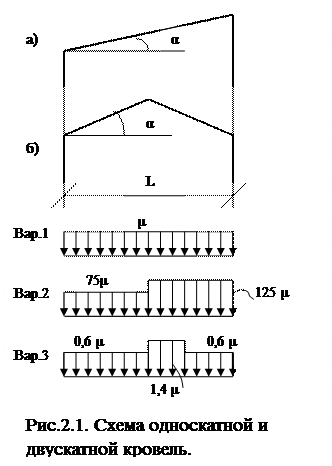 Значение коэффициента μ для зданий
Значение коэффициента μ для зданий