
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь пределов последовательностей с арифметическими операциями.Содержание книги
Поиск на нашем сайте
Связь пределов последовательностей с арифметическими операциями.
Если xn,yn – числовые последовательности, то их суммой, разностью, произведением, частным при yn¹ 0 называются соответственно последовательности {(xn± yn)},{(xnyn)},{(xn/yn}. Теорема 8(предел суммы, произведения, частного). Пусть limn®¥xn = A, limn®¥yn = B, тогда 1. limn®¥(xn± yn) = A± B; 2. limn®¥xnyn = AB; 3. limn®¥xn/yn = A/B, при B¹ 0. Теорема 9. Если limn ® ¥xn = A, limn ® ¥yn = B, и A<B, то $ N: " n>N xn<yn. Теорема 10 (о трех последовательностях). Пусть последовательности xn, yn, zn удовлетворяют при любом n>N условию: xn £ yn £ zn, причем limn ® ¥ xn = limn ® ¥ zn = A. Тогда limn ® ¥yn = A. Доказательство. Согласно определению предела " e > 0 $ N1: " n>N1 выполняется A- e < xn < A+ e " e > 0 $ N2: " n > N2, A-e < zn < A+ e Если N = max(N1,N2), тогда при n>N получим A-e<xn £ yn £ zn < A+ e. Следовательно, |yn-A|< e. Следствие 2. Если все члены последовательности принадлежат отрезку [a,b], и $ limn ® ¥xn = c, то c Î [a,b]. Бесконечно малые, бесконечно большие последовательности. Определение. Последовательность {xn} называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при
Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3,... 1, n,... не является бесконечно большой, так как при A > 1 неравенство
Определение. Последовательность {xn} называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при
Любая бесконечно малая последовательность является ограниченной.
1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. Пусть α n и β n - бесконечно малые последовательности.
2. Разница двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. Эта теорема доказывается аналогично теореме о сумме двух бесконечно малых последовательностей, только вместо 3. Бесконечно малая последовательность ограничена. Доказательство. M = max { ε,
4. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. {α n } бесконечно малая, { xn } - ограниченная.
5. Если все элементы бесконечно малой последовательности, начиная с некоторого номера, равны одному и тому же числу, то это число - ноль. Доказательство. {α n } - бесконечно малая последовательность. При n Рассмотрим ε = Положим N 1 = max 6 (а). Если { xn } - бесконечно большая последовательность, то начиная с некоторого номера определена последовательность {1 / xn }, причём она является бесконечно малой. 6 (б). Если { yn } - бесконечно малая последовательность, то начиная с некоторого номера определена последовательность {1 / en }, причём она является бесконечно большой. Доказательство. Из этого видно, что начиная с определённого номера n > 0, а это значит, что последовательность определена. {1 / xn } < Вторая часть теоремы доказывается аналогично.
Основные свойства функций 1) Четность и нечетность. Функция Пример.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. 2) Монотонность. Функция Пример.
3) Ограниченность. Функция
4) Периодичность. Функция Пример.
Предел функции по Гейне Значение
Предел функции по Коши Значение
Бесконечно малые функции Функция f (x) называется бесконечно малой функцией в точке х = х 0, если
Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x 0 – 0, x → x 0 + 0. Имеет место следующая теорема: функция f (x) в окрестности точки х 0 отличается от своего предельного значения A на бесконечно малую функцию.
Рассмотрим разность f (x) – А = α(х). Так как
то функция α(х) является бесконечно малой при x → х 0. Бесконечно большие функции Функция f (x) называется бесконечно большой функцией в точке х = x 0 (или x → x 0), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х 0 | < δ, выполняется неравенство | f (x) | > К.
и говорят, что функция стремится к бесконечности при х → х 0, или что она имеет бесконечный предел в точке х = х 0. Если же в определении выполняется неравенство f (x) > K (f (x) < – K), то пишут
и говорят, что функция имеет в точке х 0 бесконечный предел, равный + ∞ (– ∞).
Так, например, пишут (
Точки разрыва функций. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Рис. 2 Придав произвольное приращение аргументу Уравнение прямой, проходящей через точки Касательной к графику функции Для того, чтобы секущая Угловой коэффициент касательной получается путем перехода от
Таким образом, получим, что
В случае бесконечной производной Из уравнения секущей имеем:
Переходя в равенстве к пределу при Производная сложной функции Пусть функция f: [ a, b ] → [ c, d ], а функция g:[ a 1, b 1] → [ c 1, d 1], причём [ a 1, b 1] g ' (f (x 0))· f ' (x 0). Доказательство. Так как функция g (y) дифференцируема в точке у 0, то имеем Δ g (y) = g ' (y 0)·Δ y + δ(Δ y)·Δ y, где δ(Δ х) → 0 при Δ х → 0. Так как функция f (x)дифференцируема в точке х 0, то имеем Δ y = f ' (x 0 )·Δ x + ε (Δ x)·Δ x, где ε(Δ х) → 0 при Δ х → 0. Поставляя второе соотношение в первое, получим
Разделив обе части последнего соотношения на Δ х, получим
Переходя к пределу при Δ х → 0 в левой и правой части последнего равенства с учётом непрерывности рассматриваемых функций, получим g ' (f (x))| x 0 = g ' (y 0)· f ' (x 0). Что и требовалось доказать.
Дифференцируемость функции. Дифференцируемость функции Операция нахождения производной называется дифференцированием функции. Функция называется дифференцируемой в некоторой точке, если она имеет в этой точке конечную производную, и дифференцируемой на некотором множестве, если она дифференцируема в каждой точке этого множества. В силу геометрического смысла производной следующие два свойства равносильны друг другу: 1) функция
Теорема. Если функция дифференцируема в некоторой точке, она непрерывна в этой точке. Доказательство. Пусть в некоторой точке области определения функции
Запишем приращение функции в виде
и найдём
Следовательно, если
Таким образом, из дифференцируемости функции вытекает её непрерывность. Обратная теорема неверна, так как существуют непрерывные функции, которые в некоторых точках являются недифференцируемыми.
Пример 3. Функция
непрерывна в точке
Из сказанного выше следует, что непрерывность в точке x является необходимым, но не достаточным условием дифференцируемости функции в этой точке, так как из непрерывности функции в точке
Формула Лейбница
Пусть y = u·v, где u и v — некоторые функции от переменной x, имеющие производные любого порядка. Тогда
где
для k = 2 имеем
для k = 3 имеем
Правые части полученных равенств похожи на разложения различных степеней бинома (u + v) n по формуле Ньютона, но вместо показателей степени стоят числа, определяющие порядок производных, а сами функции u и v для полной аналогии с формулой Ньютона нужно рассматривать как «производные нулевого порядка»: u (0) и v (0).
Докажем, что формула справедлива при k = n + 1. Действительно, в этом случае
Здесь воспользовались свойством сочетаний
и в полученных суммах объединим попарно слагаемые, содержащие производные одинаковых порядков. После обозначения общего индекса суммирования через р, будем иметь
Так как
Теорема Ролля Пусть функция f (x) непрерывна на [ a, b ], дифференцируема на (a, b) и на концах отрезка принимает равные значения f (a) = f (b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0. Теорема Лагранжа Если функция f (x) непрерывна на замкнутом отрезке [ a, b ], дифференцируема внутри него, то существует такая точка с Î (a, b), что выполняется равенство f (b) − f (a) = f '(c)·(b − a). Д о к а з а т е л ь с т в о. Составим уравнение хорды, проходящей через точки (a, f (a)), (b, f (b)) y = f (a) + Q ·(x - a), где F (x) = f (x) − f (a) − Q ·(x − a). Очевидно, что функция F(x) удовлетворяет всем условиям теоремы Ролля. Поэтому на интервале (a, b) найдётся такая точка с, для которой F ' (c) = 0. То есть F ' (c) = f ' (c) − Q = 0. Откуда следует
И, наконец, f (b) − f (a) = f '(c)·(b − a). Теорема Коши Пусть функции f (x) и g (x) непрерывны на [ a, b ] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g (x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c Î (a, b), такая, что справедлива формула
Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g (b) = g (a), то по теореме Ролля для функции g (x) найдется точка x Î (a, b), в которой g ' (x) = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b).
Функция F (x) на [ a, b ] удовлетворяет условиям теоремы Ролля: F(x) непрерывна на [ a, b ], дифференцируема на (a, b), и, кроме того, на концах интервала принимает равные значения F (a) = F (b) = 0. По теореме Ролля для F (x) существует точка c Î (a, b), такая,что F ' (c) = 0. Так как
то
Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.
Правило Лопиталя. Первое правило Лопиталя Пусть функции f (x) и g (x) непрерывны на отрезке [ а, b ] и дифференцируемы на интервале (а, b), и пусть g ' (x) ≠ 0 всюду в (а, b). Пусть, далее, известно, что f (а) = g (а) = 0. Тогда говорят, что отношение
при х → а + 0 представляет собой неопределённость вида
то и
Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х 0 так, чтобы в интервале (а, x 0) выполнялось неравенство
Применим теорему Коши к отрезку [ а, x 0], Если х
и, следовательно, для всех х
Это означает, что Второе правило Лопиталя Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g ' (x) не обращается в нуль в (a, b). Пусть известно, что
Тогда говорят, что отношение
то и
Доказательство. Пусть А конечно. Для заданного как угодно малого числа ε > 0 выберем х 0 так, чтобы в интервале (а, x 0) выполнялось неравенство
Определим функцию D (x, x 0) из условия
Имеем
при x → a + 0. Применяя к отрезку [ x, x 0] теорему Коши, получаем, что некоторой точки с
Отсюда для всех х, для которых | D (x, x 0) - 1 | < ε, находим
Так как ε произвольно мало, то
Формула Тейлора.
Пусть функция f (x) имеет в точке а и некоторой её окрестности производные порядка n + 1. Пусть x ≠ a есть любое значение аргумента из указанной окрестности, тогда между точками а и х найдётся такая точка с, что справедлива формула
Доказательство. Положим
Функция F (x) имеет производные до порядка n + 1 вместе с функцией f (x). Функция G (x) имеет производные всех порядков, причём её производные положительны при х > a. Легко проверить, что
и поэтому F (m)(а) = f (m)(а) – f (m)(а) = 0 при m = 0, 1, …, n. Так ка
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.233 (0.009 с.) |

 все элементы xn этой последовательности удовлетворяют неравенству
все элементы xn этой последовательности удовлетворяют неравенству  .
. .
. ε > 0 N 1
ε > 0 N 1  :
:  ,
, 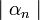 <
< 
 <
<  α n + β n
α n + β n 
 N = max (N 1
N = max (N 1 

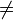 0.
0. , N *), тогда при n > N,
, N *), тогда при n > N,  - бесконечно малая.
- бесконечно малая. называется четной, если для любых значений
называется четной, если для любых значений  из области определения
из области определения  и нечетной, если
и нечетной, если  . В противном случае функция
. В противном случае функция  - четная (рис.3.3 а). т.к
- четная (рис.3.3 а). т.к  ;
б) Функция
;
б) Функция  - нечетная (рис.3.3 б).
- нечетная (рис.3.3 б). 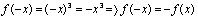 ;
в) Функция
;
в) Функция  - общего вида (рис.3.3 в).
- общего вида (рис.3.3 в).  .
.

 , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями. - на интервале
- на интервале  монотонно возрастает (рис.3.4а).
2) Функция
монотонно возрастает (рис.3.4а).
2) Функция  - на интервале
- на интервале  монотонно убывает (рис.3.4 б).
монотонно убывает (рис.3.4 б).

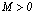 , что
, что  для любого
для любого  . В противном случает функция называется неограниченной.
. В противном случает функция называется неограниченной. - ограничена на всей числовой оси, т.к.
- ограничена на всей числовой оси, т.к.  для любого
для любого  .
. называется периодической с периодом
называется периодической с периодом  , если для любых
, если для любых  .
. , период
, период  , т.к. для любых
, т.к. для любых  .
.

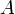 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции 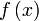 в точке
в точке  , если для любой последовательности точек
, если для любой последовательности точек  , сходящейся к
, сходящейся к  сходится к
сходится к 
 такое, что для всех аргументов
такое, что для всех аргументов  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 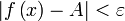

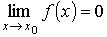
 ε > 0) (
ε > 0) (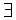 δ = δ(ε) > 0)(
δ = δ(ε) > 0)(
 ,
,
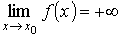 или
или 
 ,
,  ,
,  ,
,  .
.



 , так чтобы
, так чтобы  , перейдем к точке
, перейдем к точке  с абсциссой
с абсциссой  и ординатой
и ординатой  , где
, где  .
. и
и 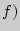 , имеет вид:
, имеет вид:  , где отношение
, где отношение  представляет собой угловой коэффициент секущей (
представляет собой угловой коэффициент секущей (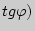 .
. в точке
в точке  , при стремлении точки
, при стремлении точки  стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел
стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел  , то есть, чтобы существовала конечная производная функции
, то есть, чтобы существовала конечная производная функции  в точке
в точке  .
.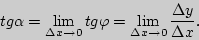
 , где
, где  - угол наклона касательной к оси
- угол наклона касательной к оси  (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции
(см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции 
 .
.
 , то есть касательная является в данном случае вертикальной прямой, проходящей через точку
, то есть касательная является в данном случае вертикальной прямой, проходящей через точку  [ c, d ]. Если функция f дифференцируема в точке х 0
[ c, d ]. Если функция f дифференцируема в точке х 0  [ a, b ], а функция g дифференцируема в точке y 0 = f (x 0)
[ a, b ], а функция g дифференцируема в точке y 0 = f (x 0) 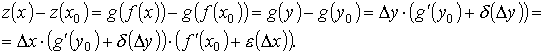
 .
. Учитывая тригонометрическое тождество
Учитывая тригонометрическое тождество
 и первый замечательный предел, получим
и первый замечательный предел, получим
 2. Вывод правила дифференцирования функции
2. Вывод правила дифференцирования функции  основывается на тригонометрическом тождестве
основывается на тригонометрическом тождестве
 и первом замечательном пределе:
и первом замечательном пределе:

 3. Для вывода правила дифференцирования функции
3. Для вывода правила дифференцирования функции  представим эту функцию в виде отношения синуса к косинусу и воспользуемся правилом дифференцирования частного от деления двух функций:
представим эту функцию в виде отношения синуса к косинусу и воспользуемся правилом дифференцирования частного от деления двух функций:
 4.Аналогично обосновывается правило дифференцирования функции
4.Аналогично обосновывается правило дифференцирования функции  :
:

 дифференцируема при
дифференцируема при  ; 2) график этой точки имеет касательную в точке
; 2) график этой точки имеет касательную в точке  , не параллельную оси ординат (т.е. с конечным угловым коэффициентом).
, не параллельную оси ординат (т.е. с конечным угловым коэффициентом).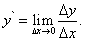


 , то и
, то и  , а это означает, что функция
, а это означает, что функция 
 , но не дифференцируема в этой точке, так как в ней график не имеет касательной. (рис. 79).
, но не дифференцируема в этой точке, так как в ней график не имеет касательной. (рис. 79). не всегда следует дифференцируемость в этой точке.
не всегда следует дифференцируемость в этой точке. .
. есть число сочетаний из n элементов по k (k = 0, 1, 2, …, n). Доказательство. Для k = 1 имеем
есть число сочетаний из n элементов по k (k = 0, 1, 2, …, n). Доказательство. Для k = 1 имеем



 . Изменим индекс суммирования во второй сумме, положив k = p - 1. В этом случае
. Изменим индекс суммирования во второй сумме, положив k = p - 1. В этом случае
 .
. и
и  , получим
, получим .
. есть угловой коэффициент хорды. Рассмотрим разность ординат функции и хорды
есть угловой коэффициент хорды. Рассмотрим разность ординат функции и хорды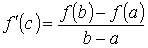 .
.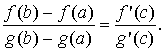
 .
. ,
, .
.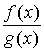
 .
.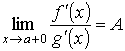 ,
, .
. .
. [ а, x 0], то существует такая точка с
[ а, x 0], то существует такая точка с 
 .
.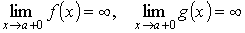 .
. .
.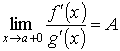 ,
, .
.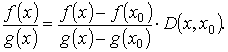 .
.
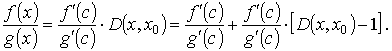

 .
. ,
, 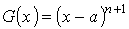 .
.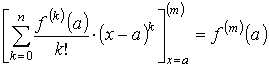 ,
,


