Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции. Её геометрический и механический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Производной функции f(x) в точке x0называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно мало). Записывается так. LimΔx→0 (Δf(x0)/Δx)=limΔx→0 ((f(x+Δx)-f(x0))/Δx)=f ` (x0) Функция f, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой на данном промежутке. Геометрический смысл производной Пусть функция
Рис. 2 Придав произвольное приращение аргументу Уравнение прямой, проходящей через точки Касательной к графику функции Для того, чтобы секущая Угловой коэффициент касательной получается путем перехода от
Таким образом, получим, что
В случае бесконечной производной Из уравнения секущей имеем:
Переходя в равенстве к пределу при Механический смысл производной Пусть материальная точка движется прямолинейно и Для определения скорости Отношение
Предел Таким образом, мгновенная скорость в момент времени
Производная суммы, произведения, частного.
Производная сложной, обратной функции. Производные сложных тригонометрических функций.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 определена в некоторой окрестности
определена в некоторой окрестности 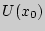 токи
токи  , непрерывна в этой точке и
, непрерывна в этой точке и  , а
, а  (рис.2).
(рис.2).
 , так чтобы
, так чтобы  , перейдем к точке
, перейдем к точке  с абсциссой
с абсциссой  и ординатой
и ординатой  , где
, где  .
. и
и 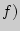 , имеет вид:
, имеет вид:  , где отношение
, где отношение  представляет собой угловой коэффициент секущей (
представляет собой угловой коэффициент секущей (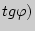 .
. , при стремлении точки
, при стремлении точки  стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел
стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел  , то есть, чтобы существовала конечная производная функции
, то есть, чтобы существовала конечная производная функции  в точке
в точке 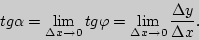
 , где
, где  - угол наклона касательной к оси
- угол наклона касательной к оси  (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции
(см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции 
 .
.
 , то есть касательная является в данном случае вертикальной прямой, проходящей через точку
, то есть касательная является в данном случае вертикальной прямой, проходящей через точку  - длина пути, проходимого за время
- длина пути, проходимого за время 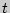 , отсчитываемого от некоторого момента времени
, отсчитываемого от некоторого момента времени  .
. в данный момент
в данный момент  , при этом приращение пути будет равно
, при этом приращение пути будет равно  .
. называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени
называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени 
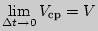 называется величиной мгновенной скорости движения в момент времени
называется величиной мгновенной скорости движения в момент времени  .
.