
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение бесконечно малых функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть α(x) и β(x) две бесконечно малые функции при x → x 0 и β(x) отлична от нуля в некоторой окрестности точки х 0 (за исключением, быть может, самой точки х 0). Если
то α(x) называется бесконечно малой более высокого порядка, чем β(x). В этом случае пишут α(x) = o(β(x)) и говорят α(x) есть о − малое от β(x).
то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = O(β(x)), (α(x) есть O - большое от β(x).
то α(x) называется бесконечно малой более низкого порядка, чем β(x).
то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x).
то α(x) является бесконечно малой n -го порядка относительно β(x).
Непрерывность функции в точке. Свойства непрерывных в точке функций. Определение 1. Функция 1) определена в точке 2) имеет конечные односторонние пределы функции при 3) эти пределы равны значению функции в точке
Определение 2. Функция Определения 1 и 2 равносильны. Свойства функций, непрерывных в точке 1. Если функции 2. Если функция Доказательство этого свойства основывается на том, что при малых приращениях аргумента 3. Если функция Свойство можно записать: Т.е. под знаком непрерывной функции можно переходить к пределу.
Точки разрыва функций. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.007 с.) |

 = 0,
= 0, ,
,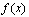 называется непрерывной в точке
называется непрерывной в точке  , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям: ;
; слева и справа;
слева и справа; .
. называется непрерывной в точке
называется непрерывной в точке  .
.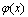 непрерывны в точке
непрерывны в точке  , произведение
, произведение  и частное
и частное  (при условии
(при условии  ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке 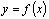 непрерывна в точке
непрерывна в точке 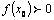 , то существует такая окрестность точки
, то существует такая окрестность точки  .
.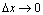 можно получить как угодно малое приращение функции
можно получить как угодно малое приращение функции  в окрестностях
в окрестностях 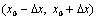 не изменится.
не изменится. непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  непрерывна в точке
непрерывна в точке  , приводящее в свою очередь к непрерывности функции
, приводящее в свою очередь к непрерывности функции  .
. ,
,






