
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монотонные последовательности, число еСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей. Определения Пусть имеется множество Последовательность
Последовательность
Последовательность
Последовательность
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей Последовательность называется строго монотонной, если она является возрастающей, либо убывающей. Очевидно, что строго монотонная последовательность является монотонной. Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно. Промежутки монотонности Может оказаться, что вышеуказанные условия выполняются не для всех номеров
(здесь допускается обращение правой границы
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел. На основе теоремы Вейерштрасса последовательность
Число е является иррациональным числом — числом, несоизмеримым с единицей, оно не может быть точно выраженным ни целым ни дробным рациональным числом.
39. Понятие функции, области определения, значений. Способы задания функции.
Определение. Если каждому элементу При этом Множество Если множество Способы задания функций: а) Аналитический способ, если функция задана формулой вида Например, функция б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента
в) Графический способ состоит в изображении графика функции - множества точек г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: Основные свойства функций 1) Четность и нечетность. Функция Пример.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. 2) Монотонность. Функция Пример.
3) Ограниченность. Функция
4) Периодичность. Функция Пример.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.21 (0.008 с.) |

 , на котором введено отношение порядка.
, на котором введено отношение порядка. элементов множества
элементов множества 



 , а лишь для номеров из некоторого диапазона
, а лишь для номеров из некоторого диапазона
 в бесконечность). В этом случае последовательность называется монотонной на промежутке
в бесконечность). В этом случае последовательность называется монотонной на промежутке  , а сам диапазон
, а сам диапазон 
 множества
множества  ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент  множества
множества  , то тогда говорят, что на множестве
, то тогда говорят, что на множестве  задана функция
задана функция  .
. обозначает закон соответствия.
обозначает закон соответствия. - областью значений функции.
- областью значений функции. задана аналитически. Не следует, однако, смешивать функцию с ее аналитическим выражением. Так, например, одна функция
задана аналитически. Не следует, однако, смешивать функцию с ее аналитическим выражением. Так, например, одна функция  имеет два аналитических выражения:
имеет два аналитических выражения:  (при
(при  ) и
) и  (при
(при  ).
). , например, таблица логарифмов, гармонические функции и т.д.
, например, таблица логарифмов, гармонические функции и т.д.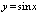 ,
,  ,
, 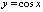 .
. плоскости, абсциссы которых есть значения аргумента
плоскости, абсциссы которых есть значения аргумента  , если
, если  и нечетной, если
и нечетной, если  . В противном случае функция
. В противном случае функция  - четная (рис.3.3 а). т.к
- четная (рис.3.3 а). т.к  ;
б) Функция
;
б) Функция  - нечетная (рис.3.3 б).
- нечетная (рис.3.3 б). 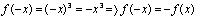 ;
в) Функция
;
в) Функция  - общего вида (рис.3.3 в).
- общего вида (рис.3.3 в).  .
.

 - на интервале
- на интервале  монотонно возрастает (рис.3.4а).
2) Функция
монотонно возрастает (рис.3.4а).
2) Функция  - на интервале
- на интервале  монотонно убывает (рис.3.4 б).
монотонно убывает (рис.3.4 б).

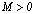 , что
, что  для любого
для любого  . В противном случает функция называется неограниченной.
. В противном случает функция называется неограниченной. - ограничена на всей числовой оси, т.к.
- ограничена на всей числовой оси, т.к.  для любого
для любого  .
. называется периодической с периодом
называется периодической с периодом  , если для любых
, если для любых  .
. , период
, период  , т.к. для любых
, т.к. для любых  .
.




