
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции. Связь с производной, геометрический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция
Таким образом, приращение функции 1) 2) Определение. Дифференциалом функции называется главная, линейная относительно
Пример. Найти приращение функции Решение. Пример. Найти дифференциал функции Решение. По формуле (7.2.) имеем Определение. Дифференциал независимой переменной
Тогда формулу (7.2) для дифференциала функции можно записать в виде:
Откуда
Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции
Инвариартность формы дифференциала. Если Рассмотрим сложную функцию Если функции Умножим обе части равенства на
Производные высших порядков.
Пусть y = f (x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:
Производные более высокого порядка (если они существуют), определяются как
Для нахождения производных высшего порядка можно использовать следующие формулы:
В частности, для производной второго и третьего порядка формула Лейбница принимает вид
Формула Лейбница
Пусть y = u·v, где u и v — некоторые функции от переменной x, имеющие производные любого порядка. Тогда
где
для k = 2 имеем
для k = 3 имеем
Правые части полученных равенств похожи на разложения различных степеней бинома (u + v) n по формуле Ньютона, но вместо показателей степени стоят числа, определяющие порядок производных, а сами функции u и v для полной аналогии с формулой Ньютона нужно рассматривать как «производные нулевого порядка»: u (0) и v (0).
Докажем, что формула справедлива при k = n + 1. Действительно, в этом случае
Здесь воспользовались свойством сочетаний
и в полученных суммах объединим попарно слагаемые, содержащие производные одинаковых порядков. После обозначения общего индекса суммирования через р, будем иметь
Так как
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.1 (0.008 с.) |

 определена на промежутке
определена на промежутке  и дифференцируема в окрестности точки
и дифференцируема в окрестности точки  ,тогда
,тогда  или по теореме о связи бесконечно малых с пределами функций имеем
или по теореме о связи бесконечно малых с пределами функций имеем  , где
, где  - бесконечно малая величина при
- бесконечно малая величина при  . Отсюда:
. Отсюда: . (7.1)
. (7.1) состоит из двух слагаемых:
состоит из двух слагаемых: - линейного относительно
- линейного относительно  , т.к.
, т.к.  ;
; - нелинейного относительно
- нелинейного относительно  .
. . (7.2)
. (7.2)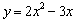 при
при  и
и  :
:
 ,
, 
 .
. .
. равен приращению этой переменной:
равен приращению этой переменной: (7.3)
(7.3) (7.4)
(7.4)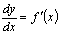 , поэтому
, поэтому  можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем
можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем  и знаменателем
и знаменателем 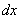 .
.
 (рис. 7.1.) возьмем произвольную точку
(рис. 7.1.) возьмем произвольную точку  . Дадим аргументу
. Дадим аргументу 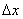 , тогда функция получает приращение
, тогда функция получает приращение  . В точке
. В точке  проведем касательную, образующую угол
проведем касательную, образующую угол  с осью
с осью  . Из треугольника
. Из треугольника  :
:  . Из
. Из  имеем:
имеем: 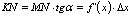 . Таким образом,
. Таким образом, 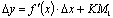 и соответствует формуле (7.1).
и соответствует формуле (7.1).
 , то из (7.4) имеем
, то из (7.4) имеем  .
. , где
, где  .
.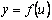 и
и  .
. . Таким образом,
. Таким образом,  .
.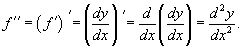




 .
. есть число сочетаний из n элементов по k (k = 0, 1, 2, …, n). Доказательство. Для k = 1 имеем
есть число сочетаний из n элементов по k (k = 0, 1, 2, …, n). Доказательство. Для k = 1 имеем



 . Изменим индекс суммирования во второй сумме, положив k = p - 1. В этом случае
. Изменим индекс суммирования во второй сумме, положив k = p - 1. В этом случае
 .
. и
и  , получим
, получим .
.


