
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гиперболические функции. Их свойства и дифференцирование.Содержание книги
Поиск на нашем сайте
В приложениях показательные функции часто встречаются в комбинациях
Вследствие этого эти комбинации получили особые названия. Первую называют гиперболическим косинусом, обозначая его через ch x (cos hyp х), а вторую - гиперболическим синусом, обозначая его через sh x (sin hyp x). Таким образом имеем
Эти обозначения и названия введены по аналогии с известными формулами Эйлера для тригонометрических функций
Исходя из равенств, определяющих sh x и ch x, можно развить теорию гиперболических функций. Формулы ее весьма схожи с формулами обыкновенной тригонометрии. Нетрудно проверить, что ch (- х) = ch х, sh (- х) = - sh x, ch xi = cos x, sh xi = i sin x, ch2 x - sh2 x = 1. Рассматривают также гиперболические тангенс и котангенс, определяя их с помощью равенств
ch (x + y) = ch x ·ch у + sh x ·sh у, Нетрудно видеть, что sh 2 х = 2 sh х ·ch x, ch 2 x = ch2 x + sh2 x, В приложениях приходится рассматривать и обратные гиперболические функции. Если положим ch x = u и sh v = v, то x = Arch u = = arsh v. Здесь Ar происходит от латинского слова «area» Из этих двух функций первая двузначна, а вторая однозначна. Решая уравнения
относительно ех, находим
откуда
Следовательно,
Впервой из этих двух формул допустимы перед корнем оба знака. Во второй - только один, ибо при отрицательном знаке логарифм перестает быть вещественным.
Дифференцируемость функции. Дифференцируемость функции Операция нахождения производной называется дифференцированием функции. Функция называется дифференцируемой в некоторой точке, если она имеет в этой точке конечную производную, и дифференцируемой на некотором множестве, если она дифференцируема в каждой точке этого множества. В силу геометрического смысла производной следующие два свойства равносильны друг другу: 1) функция
Теорема. Если функция дифференцируема в некоторой точке, она непрерывна в этой точке. Доказательство. Пусть в некоторой точке области определения функции
Запишем приращение функции в виде
и найдём
Следовательно, если
Таким образом, из дифференцируемости функции вытекает её непрерывность. Обратная теорема неверна, так как существуют непрерывные функции, которые в некоторых точках являются недифференцируемыми.
Пример 3. Функция
непрерывна в точке
Из сказанного выше следует, что непрерывность в точке x является необходимым, но не достаточным условием дифференцируемости функции в этой точке, так как из непрерывности функции в точке
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.005 с.) |





 .
.
 ,
, .
. .
.

 дифференцируема при
дифференцируема при  ; 2) график этой точки имеет касательную в точке
; 2) график этой точки имеет касательную в точке  , не параллельную оси ординат (т.е. с конечным угловым коэффициентом).
, не параллельную оси ординат (т.е. с конечным угловым коэффициентом).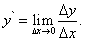


 , то и
, то и  , а это означает, что функция
, а это означает, что функция 
 , но не дифференцируема в этой точке, так как в ней график не имеет касательной. (рис. 79).
, но не дифференцируема в этой точке, так как в ней график не имеет касательной. (рис. 79). не всегда следует дифференцируемость в этой точке.
не всегда следует дифференцируемость в этой точке.


