
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числова функція. Основні властивості функції та її графік.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Числова функція. Основні властивості функції та її графік. Числовою функцією з областю визначення
Множину всіх значень незалежної змінної Основними способами задання функції є аналітичний (за допомогою формули), графічний і табличний. Функція
2. Функція Синусом числа
Крива, яка є графіком функції у = sin x, називається синусоїдою. Властивості функції
Графік функції симетричний відносно початку координат.
з віссю О з віссю О
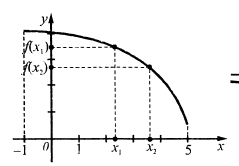
функція зростає на кожному з проміжків і спадає на кожному з проміжків
3. Функція Косинусом числа
Графіком функції є косинусоїда. Властивості функції
з віссю О
функція зростає на кожному з проміжків і спадає на кожному з проміжків
4. Функція Тангенсом числа
Графіком функції є тангенсоїда. Властивості функції 1. Область визначення функції – 2. Множина значень функції – 3. Непарна функція: Графік функції симетричний відносно початку координат. 4. Періодична функція з найменшим додатним періодом 5. Точки перетину з осями координат: з віссю О з віссю О 6. Проміжки знакосталості:
7. Проміжки монотонності: функція зростає на кожному з проміжків 8. Найменших значень функція немає. 9. Найбільших значень функція немає.
Залежність між тригонометричними функціями одного й того самого аргументу. sin2 α + cos2 α = l – основна тригонометрична тотожність. З цієї формули можна виразити sin α через cos α і навпаки: За означенням тангенса і котангенса:
Перемноживши ці рівності, одержимо З цієї рівності можна виразити tg α через ctg α і навпаки:
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на соs2α ≠ 0:
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на sіn2 α ≠ 0:
Тригонометричні функції подвійного аргументу. Тригонометричні функції подвійного аргументу виражають тригонометричні функції аргументу 2 Із формули
Аналогічно із формули
Якщо замінити за допомогою основної тригонометричної тотожності
Із формули
Формули зведення. Формулами зведення називаються співвідношення, за допомогою яких значення тригонометричних функцій аргументів Для того щоб записати будь-яку з них, можна користуватися таким правилом: 1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < α < 2) Якщо в лівій частині формули кут дорівнює Наприклад: За допомогою формул зведення знаходження значень тригонометричних функцій будь-якого кута можна звести до знаходження тригонометричних функцій гострого кута.
8. Тригонометричні рівняння. Розв’язування рівняння Рівняння, які містять змінну лише під знаком тригонометричної функції, називаються тригонометричними рівняннями. Арксинусом числа
Рівняння
Якщо Якщо
Враховуючиперіодичність
Ці дві формули можна записати у вигляді однієї формули:
При парному
9. Тригонометричні рівняння. Розв’язування рівняння Рівняння, які містять змінну лише під знаком тригонометричної функції, називаються тригонометричними рівняннями. Арккосинусом числа
Рівняння
Якщо Якщо Враховуючиперіодичність
10. Тригонометричні рівняння. Розв’язування рівняння Рівняння, які містять змінну лише під знаком тригонометричної функції, називаються тригонометричними рівняннями. Арктангенсом числа
Рівняння Окремі випадки:
Числова функція. Основні властивості функції та її графік. Числовою функцією з областю визначення
Множину всіх значень незалежної змінної Основними способами задання функції є аналітичний (за допомогою формули), графічний і табличний. Функція
2. Функція Синусом числа
Крива, яка є графіком функції у = sin x, називається синусоїдою. Властивості функції
Графік функції симетричний відносно початку координат.
з віссю О з віссю О
функція зростає на кожному з проміжків і спадає на кожному з проміжків
3. Функція Косинусом числа
Графіком функції є косинусоїда. Властивості функції
з віссю О
функція зростає на кожному з проміжків і спадає на кожному з проміжків
4. Функція Тангенсом числа
Графіком функції є тангенсоїда. Властивості функції 1. Область визначення функції – 2. Множина значень функції – 3. Непарна функція: Графік функції симетричний відносно початку координат. 4. Періодична функція з найменшим додатним періодом 5. Точки перетину з осями координат: з віссю О з віссю О 6. Проміжки знакосталості:
7. Проміжки монотонності: функція зростає на кожному з проміжків 8. Найменших значень функція немає. 9. Найбільших значень функція немає.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.110 (0.011 с.) |

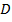 називають таку залежність, при якій кожному числу
називають таку залежність, при якій кожному числу 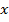 з множини
з множини 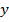 :
: 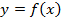 .
.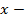 незалежна змінна або аргумент,
незалежна змінна або аргумент,  залежна змінна або функція.
залежна змінна або функція.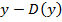 . Множину значень функції, яких вона набуває при всіх значеннях
. Множину значень функції, яких вона набуває при всіх значеннях 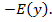
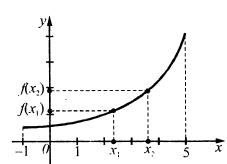
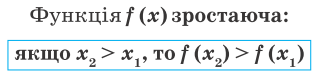



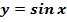 , її графік і властивості.
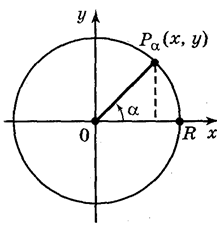
, її графік і властивості.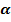 називається ордината точки
називається ордината точки 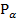 одиничного кола, в яку переходить початкова точка
одиничного кола, в яку переходить початкова точка 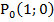 при повороті навколо центра кола на кут
при повороті навколо центра кола на кут  радіан -
радіан -  .
.

 .
.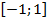 :
: 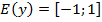 .
.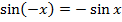 .
. 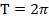 :
: 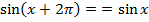 .
.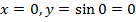 , тобто графік проходить через (0;0) – початок координат;
, тобто графік проходить через (0;0) – початок координат;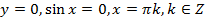 .
.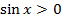 , якщо
, якщо 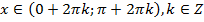 – І і ІІ чверті на одиничному колі;
– І і ІІ чверті на одиничному колі;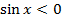 , якщо
, якщо 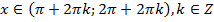 – ІІІ і І
– ІІІ і І 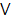 чверті на одиничному колі.
чверті на одиничному колі.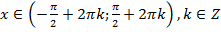
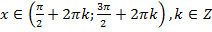 .
.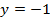 , якщо
, якщо 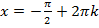 .
.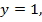 якщо
якщо 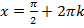 .
.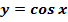 , її графік і властивості.
, її графік і властивості.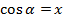 .
.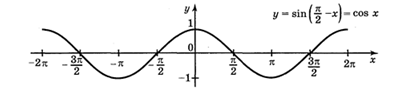
 . Графік функції симетричний відносно осі О
. Графік функції симетричний відносно осі О  .
. ; з віссю О
; з віссю О 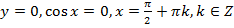 .
.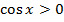 , якщо
, якщо  , якщо
, якщо 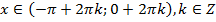
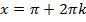 .
. .
. , її графік і властивості.
, її графік і властивості.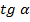 :
:  .
.
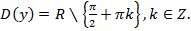
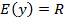 .
.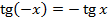 .
.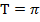 :
: 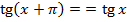 .
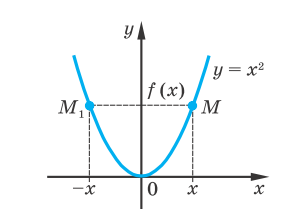
.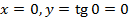 , тобто графік проходить через початок координат;
, тобто графік проходить через початок координат;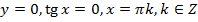 .
.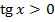 , якщо
, якщо  – І і ІІI чверті на одиничному колі;
– І і ІІI чверті на одиничному колі;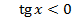 , якщо
, якщо  – ІІ і І
– ІІ і І 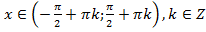 .
.

 ·
·  = l
= l
 , де де
, де де 
 , де
, де 
 при
при  , маємо:
, маємо:
 при
при  одержуємо:
одержуємо:
 функцію
функцію  на
на  або
або  на
на 

 при
при 
 , виражаються через функції кута α.
, виражаються через функції кута α. .
. ± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується.
± α, то синус замінюється на косинус, тангенс — на котангенс і навпаки. Якщо кут дорівнює π ± α, то заміна не виконується. ;
; 

 .
. називається таке число (кут) із проміжку
називається таке число (кут) із проміжку  , синус якого дорівнює
, синус якого дорівнює  .
.

 , то рівняння
, то рівняння  не має розв´язків, оскільки
не має розв´язків, оскільки  для будь – якого
для будь – якого  , то враховуючи те, що синус – це ордината точки одиничного кола, маємо: ординату, рівну
, то враховуючи те, що синус – це ордината точки одиничного кола, маємо: ординату, рівну 
 , маємо:
, маємо:

 маємо
маємо  , при непарному
, при непарному 
 .
.
 .
. , косинус якого дорівнює
, косинус якого дорівнює 

 не має розв´язків, оскільки
не має розв´язків, оскільки  для будь – якого
для будь – якого 
 , дістанемо множину розв´язків рівняння
, дістанемо множину розв´язків рівняння  :
:

 .
. називається таке число (кут) із проміжку
називається таке число (кут) із проміжку  , тангенс якого дорівнює
, тангенс якого дорівнює 





