
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Узагальнена схема обчислення індуктивної функції.Содержание книги
Поиск на нашем сайте
Будується індуктивне розширення F вихідної функції, яке дозволяє ціною збільшення запам'ятовуваної інформації про ланцюг ω (в F(ω) інформації більше ніж в f (ω)) застосуємо схему обчислення індуктивної функції до F(ω), а потім просто знайти Нехай Означення 10 .3 Мінімальним індуктивним розширенням функції f: Мінімальні індуктивні розширення добрі тим, що зменшують кількість додаткової інформації, яка повинна бути запам'ятована на кожному кроці для забезпечення можливості переобчислення функції на подовженому ланцюгу. Для будь-якої функції на просторі послідовностей існує і єдине (у певному сенсі), її мінімальне індуктивне розширення. Доведення цього факту проведемо в два етапи, спочатку переконавшись у єдиності розширення. Теорема 10.2 Мінмальне індуктивне розширення будь-якої функції f: Доведення. Нехай для функції f: Візьмемо довільний елемент Критерій мінімальності Перед тим, як сформулювати критерій мінімальності, доведемо існування мінімального індуктивного розширення. Теорема 10.3 Мінімальне індуктивне розширення для будь-якої функції f: Доведення. Для доведення теореми побудуємо в три етапи канонічне мінімальне індуктивне розширення Перший етап. Розглянемо на множині ланцюгів 1) 2) 3) Рефлексивність, симетричність і транзитивність відношення випливають відповідно з рефлексивності, симетричності і транзитивності відношень рівності. Так як Властивість 3) негайно випливає із визначення відношення Другий етап. Побудуємо простір Переписавши властивість 2) в еквівалентному вигляді
Покажемо, що Визначимо проекцію Так як Третий етап. Нам залишилося показати, що побудоване канонічне індуктивне розширення є мінімальним. Сюр'єктивність Припустимо наступне, що існує Визначимо проекцію Нехай Рівність Побудоване в процесі доведення цієї теореми канонічне індуктивне розширення дозволяє переконатися в істинності наступного критерію мінімальності. Теорема 10.4 Критерій мінімальності. Індуктивне ( Доведення. Необхідність першої умови критерію випливає безпосередньо з визначення мінімальності. Друга умова виконана за побудовою для канонічного мінімального індуктивного розширення Для доведення достатності розглянемо канонічне мінімальне індуктивне розширення Критерій буде доведений, якщо ми покажемо, що відображення Сюр'єктивність
Отже, відображення
Доведемо, що функція
де
отримаємо Мінімальні індуктивні розширення володіють перевагою звести до мінімуму ту додаткову інформацію, яка необхідна для індуктивного переобчислення вихідної функції. Інакше ця властивість може бути сформульована наступним чином. Теорема 10.5 Для довільної функції
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.233.198 (0.007 с.) |

 .
. і
і 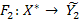 - два індуктивних розширення функції
- два індуктивних розширення функції  . Будемо говорити, що
. Будемо говорити, що  , якщо
, якщо  таке, що
таке, що 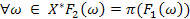 .
. , називається індуктивне розширення
, називається індуктивне розширення  таке, що 1)
таке, що 1)  (
( - сюр’єктивне); 2) для будь-якого індуктивного розширення F функції f виконано
- сюр’єктивне); 2) для будь-якого індуктивного розширення F функції f виконано  .
. і
і  . Тоді в силу їх мінімальності маємо
. Тоді в силу їх мінімальності маємо  і
і 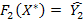 .Так як
.Так як  - мінімальне), то
- мінімальне), то  таке, що
таке, що  . З іншого боку,
. З іншого боку, 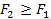 і
і  таке, що
таке, що 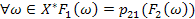 . Для доведення теореми необхідно показати, що відображення
. Для доведення теореми необхідно показати, що відображення  і
і  бієктивні. Розглянемо композицію цих відображення
бієктивні. Розглянемо композицію цих відображення  і
і  і доведемо, що вони є тотожними відображеннями множин
і доведемо, що вони є тотожними відображеннями множин  і
і  відповідно (із цього слідує бієктивне відображення
відповідно (із цього слідує бієктивне відображення  . Із сюр’єктивності
. Із сюр’єктивності  випливає, що знайдеться ланцюг
випливає, що знайдеться ланцюг  , такий, що
, такий, що  і тому
і тому  . Отримана рівність показує, що \
. Отримана рівність показує, що \  - тотожне відображення. Розглядаючи довільні елементи
- тотожне відображення. Розглядаючи довільні елементи  , аналогічно отримуємо, що
, аналогічно отримуємо, що 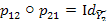 , що і закінчує доведення теореми.
, що і закінчує доведення теореми. бінарне відношення
бінарне відношення  , задане формулою
, задане формулою  , і покажемо, що
, і покажемо, що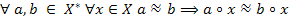 ;
; .
.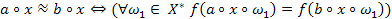 , то взявши в якості ланцюга
, то взявши в якості ланцюга 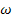 , що фігурує у визначенні відношення
, що фігурує у визначенні відношення  , переконуємося в істинності другої властивості.
, переконуємося в істинності другої властивості. .
. та відображення
та відображення  В якості
В якості  , що можна зробити в силу властивості 1). Домовимося позначати клас еквівалентності, який містить ланцюг
, що можна зробити в силу властивості 1). Домовимося позначати клас еквівалентності, який містить ланцюг  і визначимо відображення
і визначимо відображення  формулою
формулою  .
. , з критерію індуктивності робимл висновок, що відображення
, з критерію індуктивності робимл висновок, що відображення  .
. формулою
формулою  . Коректність цього визначення випливає із властивості 3) - якщо два ланцюжки
. Коректність цього визначення випливає із властивості 3) - якщо два ланцюжки  належать одному класу єквівавлентності, то значення функції
належать одному класу єквівавлентності, то значення функції 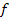 на них співпадає.
на них співпадає.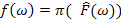 для довільного ланцюга
для довільного ланцюга  – інше індуктивне розширення вихідної функції
– інше індуктивне розширення вихідної функції 
 формулою
формулою  , де
, де  при відображенні
при відображенні  . Перевіримо коректність даного визначення.
. Перевіримо коректність даного визначення. . Тоді в силу індуктивності
. Тоді в силу індуктивності  , а так як
, а так як  – індуктивне розширення функції
– індуктивне розширення функції  . Отримана рівність може бути переписана у вигляді
. Отримана рівність може бути переписана у вигляді 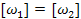 , яка показує коректність визначення проекції
, яка показує коректність визначення проекції  .
. для довільного ланцюга
для довільного ланцюга  . Теорема повністю доведена.
. Теорема повністю доведена. – мінімальне
– мінімальне 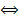
 )
)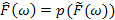 для довільного ланцюга
для довільного ланцюга  та, скориставшись сюр'єктивністю
та, скориставшись сюр'єктивністю  із
із  . Так як
. Так як  , то в силу даної нам умови
, то в силу даної нам умови 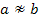 , що еквівалентно нерівності
, що еквівалентно нерівності  .
. перетворює в різні ж
перетворює в різні ж , що і вимагалося довести.
, що і вимагалося довести. , визначена за формулою
, визначена за формулою
 , є мінімальним індуктивним розширенням для
, є мінімальним індуктивним розширенням для  середнє арифметичне елементів послідовності. Для доведення сюр'єктивності функції F предявимо прообраз довільного елемента
середнє арифметичне елементів послідовності. Для доведення сюр'єктивності функції F предявимо прообраз довільного елемента  . Ним буде ланцюг з n елементів, перший з яких дорівнює s, а решта – нулеві. Для того щоб перевірити другу умову критерію мінімальності, необхідно переконатися в тому, що
. Ним буде ланцюг з n елементів, перший з яких дорівнює s, а решта – нулеві. Для того щоб перевірити другу умову критерію мінімальності, необхідно переконатися в тому, що 
 та або
та або  або
або  . Якщо для порожнього ланцюга
. Якщо для порожнього ланцюга  виконується
виконується  , то все доведено. Інакше маємо
, то все доведено. Інакше маємо  . Візьмемо тепер в якості
. Візьмемо тепер в якості  із системи
із системи

 , що суперечить припущенню. Це завершує доведення мінімальності F.
, що суперечить припущенню. Це завершує доведення мінімальності F.


