
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предикати і документування програмСодержание книги
Поиск на нашем сайте Предикати тут нам будуть потрібні як інструмент формулювання певних тверджень про прогрпми і програмні змінні. Розглянемо декілька прикладів. Приклад 9.1. Запишіть предикат який стверджує,що якщо i < j, а m > n, то u = v. Розв’язок. i < j ∧ m > n ⇒ (u = v).
Приклад 9.2. Запишіть предикат який стверджує, що жодне із наступних тверджень не є істинним: a < b, b < c і x = y.. Розв’язок. P1 = ((a < b) = F)∧((b < c) = F)∧((x = y) = F), P2 =!(a < b)∧!(b < c)∧!(x = y) і P3 = a > b ∧ b > c ∧ x≠ y. Всі три рішення еквівалентні. Третє – найкоротше, його і будемо використовувати. В наступних прикладах матимемо справу із масивами. Введемо позначення вирізки із масива b[0..m−1], в якій будуть знаходиться всі елементи з індексами від j до k включно, символами b[j..k]. У випадку, коли індекс виходить за межі масива, тобто j > k, k < 0 або j > m, вірізка є пустою множиною.
Приклад 9.3. Запишіть предикат який стверджує, що для масива b[0..n − 1] довжини n > 0 усі елементи вирізки b[j..k] є нульовими. Розв’язок. Використаємо квантор узагальнення: ∀i j ≤ i < k +1 b[i] = 0.
Приклад 9.4. Запишіть предикат який стверджує, що для масива b[0..n − 1] довжини n > 0 усі елементи вирізки b[j..k] жоден елемент не є нульовим. Розв’язок. ∀i j ≤ i < k + 1 b[i] ≠ 0.
Задача переведення висловлення з природної мови на мову предикатів не завжди є однозначною, але це і є однією із причин його використаня. высказывания с естественного языка на язык преди-
Приклад 9.5. Запишіть предикат який стверджує, що для масива b[0..n − 1] довжини n > 0 деякі із елементів вирізки b[j..k] є нульовими. Розв’язок. Цевисловлення можна розуміти двозначно: воно може означати, що ввирізці існує хоча б один нулевий елемент, а може означати і те, що в ній мінімум два елементи ненульові: P1 = ∃i j ≤ i < k + 1 b[i] = 0 і P2 = ∃i j ≤ i < k + 1 ∃m (j ≤ m < k + 1 ∧ m ≠ i)(b[i] =0) ∧ (b[m] = 0).
Ось деякі приклади із математики.
Приклад 9.6. Запишіть предикат, який стверджує, що фунція f: {1, 2, 3, 4, 5} → {1, 2, 3, 4, 5} є сюр’єктвною і заперечення цього факту. Розв’язок. Згідно визначення маємо P = (∀y ∈ {1, 2, 3, 4, 5} ∃x ∈ {1, 2, 3, 4, 5} y = f(x)). Побудуємо заперечення і спростимо його за законами еквівалентності !P = (!(∀y ∈{1, 2, 3, 4, 5} ∃x ∈ {1, 2, 3, 4, 5} y = f(x))) = (∃y ∈ {1, 2, 3, 4, 5}!(∃x ∈{1, 2, 3, 4, 5} y = f(x))) = (∃y ∈ {1, 2, 3, 4, 5} ∀x ∈ {1, 2, 3, 4, 5}!(y = f(x))) = (∃y ∈ {1, 2, 3, 4, 5} ∀x ∈ {1, 2, 3, 4, 5} y ≠ f(x)).
Приклад 9.7. Запишіть предикат, який стверджує, що фунція f: {1, 2, 3, 4, 5} → {1, 2, 3, 4, 5} всі елементи менші 4 не збільшує і заперечення цього факту. Розв’язок. P = (∀x ∈ {1, 2, 3} f(x) ≤ x).
!P =!(∀x ∈ {1, 2, 3} f(x) ≤ x) = (∃x ∈ {1, 2, 3} f(x) > x).
У текст програми іноді потрібно включат предикати, які дозволяють людині перевіряти хід виконання програми. У випадку, коли ці предикати відносяться тільки до людини, вони оформляються у вигляді коментарів. Але часто потрібно покласти перевірку цих предикатів на комп у процесі виконання програми (від лагодження програми). У різних мовах програмування ця можливість реалізована по своєму. Наприклад в мові C можна скористатися макросом assert(P), який у випадку хибності свого аргумента (предиката P) зразу ж зупиняє виконання програми, повідомляючи про причину зупинки обробки програми. Механізм роботи із виключеннями і оператор if дозволяє легко реалізувати відповідну конструкцію на Java. Ось простий приклад:
Приклад 9.8. Напишіть програму, яка містить перевірку істинності твердження про додатність введеного з клавіатури цілого числа.
Текст програми.
public class Assert { public static void main(String[] args) throws Exception { int n = Xterm.inputInt("Введите n -> "); if (n <= 0) throw new Exception("n <= 0"); Xterm.println("n = " + n); } } При вводенні від’ємного числа програма зупиняє роботу і друкує повідомлення:
java.lang.Exception: n<=0 at Assert.main(Assert.java:4)
Зрозуміло, що багаті можливості мови дозволяють більш красиво і ефективніше реалізувати цю перевірку, та наразі на цьому ми зупинятися не будемо. 9.1. Специфікація програми і перетворювач предикатів Для того, щоб доводити правильність програм необхідно передусім дати строге визначення поняттю правильна програма. Ясно, що воно залежить не лише від результату який має бути отриманий в процесі виконання програми, але і від того, в яких умовах починається її виконання.
Визначення 9.1 Специфікацією Під програмою S у цьому визначенні може розумітися один або декілька окремих операторів або ж дійсно ціла велика програма.
Визначення 9.2 Предикат Q називається передумовою або вхідним твердженням S; R -- постумовою або вихідним твердженням програми S.
Оскільки специфікація програми є предикатом, то вона може бути істинною, а може бути і хибною. Можлива і така ситуація, коли в деяких станах вона істинна, а в інших -- хибна. Ось відповідні приклади.
· Специфікація · специфікація · а специфікація
Специфікація програми є єдиним коректним способом постановки завдання. Тільки чітко сформулювавши перед- і постумови, можна обговорювати потім правильність програми.
Визначення 9.3 Програма
З практичної точки зору особливу заціавленість представляють програми, які дозволяють отримати потрібний результат за мінімальних вимог до початкових умов а також програми, що дозволяють досягти як можна більшого при фіксованій передумові. Слабка передумова -- предикат, що описує максимально широку множину станів змінних програми Для цілей доведення правильності програм особливо важливий наступний предикат.
Визначення 9.4. Слабка передумова
wp ("if (x> = y) z = x; else z = y; ", z = y +1) = (x = y + 1), бо тільки за такої початкової умови після виконання програми змінна z стане рівною y + 1.
Зауважимо, що з визначень специфікації програми та її найслабшої передумови випливає наступне твердження.
Твердження 9.1.. {Q} S {R} = (Q
Доведемо акуратно дистрибутивність кон'юнкції. Для доведення еквівалентності досить показати, що з умови
, розглянемо довільне стан s, що задовольняє умові
Для доведення зворотньої імплікації Закон монотонності доведіть самостійно, а от з приводу останньої властивості перетворювача предикатів - дистрибутивності диз'юнкції - треба зробити деякі зауваження. Справа в тому, що якщо у якості S розглянути операцію викидання монети, яка може завершитися або випаданням герба (G), або решки (R), тоді Якщо S є недетермінованою, то еквівалентність в законі дистрибутивності диз'юнкції перетворюється на імплікації. Однак для програм S, реалізованих за допомогою більшості мов програмування, подібна ситуація неможлива.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.149.236 (0.01 с.) |

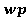
 програми
програми  , де
, де  і R-- предикати, називається предикат, який означає, що якщо виконання S почалося в стані що задовольняє Q то маємо гарантію, що виконання завершиться через скінчений час в стані, що задовольнить R.
і R-- предикати, називається предикат, який означає, що якщо виконання S почалося в стані що задовольняє Q то маємо гарантію, що виконання завершиться через скінчений час в стані, що задовольнить R. "i++;"
"i++;"  є тавтологією,
є тавтологією, істинна при
істинна при 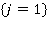 і помилкова в інших станах.
і помилкова в інших станах. , якщо специфікація {Q} S {R} є тавтологією.
, якщо специфікація {Q} S {R} є тавтологією.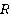 . Найсильніша постумова -- предикат, що описує максимально сильні обмеження на стан змінних програми, які можуть бути отримані при цій передумові.
. Найсильніша постумова -- предикат, що описує максимально сильні обмеження на стан змінних програми, які можуть бути отримані при цій передумові.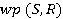 - предикат, який представляє множину всіх станів змінних програми
- предикат, який представляє множину всіх станів змінних програми  , тому що якщо змінна задовольняла умові
, тому що якщо змінна задовольняла умові 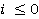 , то після виконання програми "i = i + 1;" вона дійсно буде задовольняти нерівності
, то після виконання програми "i = i + 1;" вона дійсно буде задовольняти нерівності  .
. ), тому що y дорівнюватиме максимуму з чисел x і y (а саме такою буде z після виконання програми "if (x> = y) z = x, else z = у; ") тоді і тільки тоді, якщо саме змінна y має більше значення.
), тому що y дорівнюватиме максимуму з чисел x і y (а саме такою буде z після виконання програми "if (x> = y) z = x, else z = у; ") тоді і тільки тоді, якщо саме змінна y має більше значення. (S, R))
(S, R)) ) називають
) називають  коли фіксують програму S і розглядають
коли фіксують програму S і розглядають  має такі властивості:
має такі властивості: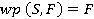 (закон виключеного дива);
(закон виключеного дива); (дистрибутивність кон'юнкції);
(дистрибутивність кон'юнкції); (закон монотонності);
(закон монотонності); (дистрибутивність диз'юнкції).
(дистрибутивність диз'юнкції).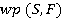 описує таку множину початкових умов, за яких виконання програми
описує таку множину початкових умов, за яких виконання програми  завершиться через обмежений час в стані, що задовольняє F, тобто ні в якому стані. Цього, звичайно, бути не може, що й пояснює назву властивості - закон виключеного дива.
завершиться через обмежений час в стані, що задовольняє F, тобто ні в якому стані. Цього, звичайно, бути не може, що й пояснює назву властивості - закон виключеного дива. , що стоїть в лівій частині, випливає умова wp (S, Q Λ R), розміщена в правій, і навпаки. Для доведення імплікації
, що стоїть в лівій частині, випливає умова wp (S, Q Λ R), розміщена в правій, і навпаки. Для доведення імплікації

 .
. ⟹
⟹  розглянемо стан s, який задовольняє умові
розглянемо стан s, який задовольняє умові  . Тоді виконання
. Тоді виконання  що задовольняє
що задовольняє  . Але будь-яке таке
. Але будь-яке таке 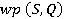 та
та  , що і закінчує доведення.
, що і закінчує доведення.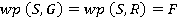 , тому що не можна гарантовано передбачити результат кидання ні за яких початкових умов. З іншого боку
, тому що не можна гарантовано передбачити результат кидання ні за яких початкових умов. З іншого боку 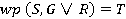 , так як завжди випаде або герб, або решка.
, так як завжди випаде або герб, або решка.


