
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема обчислення інваріантної функціїСодержание книги
Поиск на нашем сайте
Найпростішим прикладом інваріантної функції є добре відома ще з середньої школи функція
Найбільший спільний дільник двох цілих чисел (greatest common divisor,
Для обчислення значення T-інваріантної функції F в точці Схема обчислення інваріантної функції. Багаторазово виконується перетворення T, що дає послідовність точок Рисунок 9.3.відображає графічну ілюстрацію цієї схеми.
Рис. 9.3. Схема обчислення інваріантної функції
В якості ілюстрації застосування схеми обчислення інваріантної функції розглянемо наступну задачу.
ЗАВДАННЯ 9.25. Напишіть програму, що знаходить найбільший спільний дільник gcd (x, y) двох цілих невід'ємних чисел x і у не рівних одночасно нулю. Скористайтеся наступними властивостями найбільшого загального дільника (не забудьте навчитися доводити всі ці властивості):
В якості перетворення
Таким чином, нам відомі інваріант i Текст програми: public class Gcd { public static void main(String[] args) throws Exception { int x = Xterm.inputInt("x -> "); int y = Xterm.inputInt("y -> "); Xterm.print("gcd(" + x + "," + y + ") ="); while ((x!= 0) && (y!= 0)) { if (x >= y) x -= y; else y -= x; } Xterm.println(" " + (x+y)); }}Зверніть увагу на той факт, що в побудованій програмі не знадобилося наявність змінної, відповідальної за значення інваріантної функції
ЗАВДАННЯ 9.26. Напишіть програму, перемножуються два цілих числа, одне з яких невід'ємне, без використання операції множення. Точні перед- і постумови необхідної програми, тимчасова складність якої не повинна перевершувати При написанні програми величини а і b змінювати не дозволяється. Скористайтеся тим, що функція
є інваріантної щодо перетворення
що задається формулою T(x, y, z) = (2x, y/2, z), якщо у – парне, T(x, y, z) = (x, y − 1, z + x), в іншому випадку. У цьому випадку
Таким чином, нам відомі інваріант
Текст програми: public class MulInv { public static void main(String[] args) throws Exception { int a = Xterm.inputInt("a -> "); int b = Xterm.inputInt("b -> "); int x = a, y = b, z = 0; while (y > 0) { if ((y&1) == 0) { y >>>= 1; x += x; } else { y -= 1; z += x; } } Xterm.println("a * b = " + z); }}
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.102.88 (0.009 с.) |

 ту підмножину множиниX, де P(x) = T. Якщо існує перетворення
ту підмножину множиниX, де P(x) = T. Якщо існує перетворення  таке, що
таке, що  , то функція F називається T -інваріантною або просто інваріантною функцією.
, то функція F називається T -інваріантною або просто інваріантною функцією. ,.
,.  Вона є T -інваріантною щодо перетворення T: R → R, T(x) = x + 2π,
Вона є T -інваріантною щодо перетворення T: R → R, T(x) = x + 2π,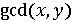 або просто НОД (x, y)) інваріантний щодо перетворення
або просто НОД (x, y)) інваріантний щодо перетворення 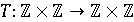 , що задається формулою
, що задається формулою
 не визначена в точці (0,0).
не визначена в точці (0,0). застосовується наступна схема.
застосовується наступна схема. Якщо чергова точка
Якщо чергова точка  попадaет в підмножину
попадaет в підмножину  , то ітерації завершуються. За визначенням інваріантної функції
, то ітерації завершуються. За визначенням інваріантної функції 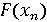 легко обчислюється і збігається з шуканим
легко обчислюється і збігається з шуканим 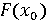 ..
..
 і умова продовження циклу
і умова продовження циклу  . Тіло циклу S конструюється, як програмна реалізація відомого перетворення T, а написання S1, що обчислює
. Тіло циклу S конструюється, як програмна реалізація відомого перетворення T, а написання S1, що обчислює  Рішення. Якщо через
Рішення. Якщо через  позначити множину всіх невід'ємних цілих чисел, які представлені в ЕОМ, то
позначити множину всіх невід'ємних цілих чисел, які представлені в ЕОМ, то 

 ,
,  .
. →X можна взяти
→X можна взяти
 умова продовження
умова продовження  . Початкові присвоювання S0 в даному випадку не потрібні, тіло циклу S пишеться за визначенням T, a програма S1, що обчислює
. Початкові присвоювання S0 в даному випадку не потрібні, тіло циклу S пишеться за визначенням T, a програма S1, що обчислює  , реалізується за допомогою справедливою для цих значень аргументу формули
, реалізується за допомогою справедливою для цих значень аргументу формули 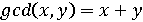 .
. , такі:
, такі: 

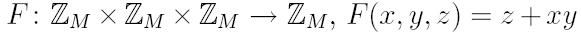
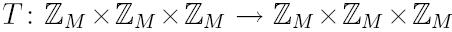 ,
, ,
,  ,
,  ,
,  . Функція F та перетворення T задані в умові завдання.
. Функція F та перетворення T задані в умові завдання.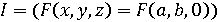 і умова продовження
і умова продовження 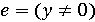 . Початкові присвоювання S0 очевидні ("x = a; y = b; z = 0;"), тіло циклу S пишеться за визначенням T, a програма S1, що обчислює F(x, y, z) для
. Початкові присвоювання S0 очевидні ("x = a; y = b; z = 0;"), тіло циклу S пишеться за визначенням T, a програма S1, що обчислює F(x, y, z) для  , у цьому випадку вироджується в порожній оператор ";", тому що для цих значень аргументу
, у цьому випадку вироджується в порожній оператор ";", тому що для цих значень аргументу  . У результаті отримуємо вже знайому нам програму.
. У результаті отримуємо вже знайому нам програму.


