
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення простих операторів мови JavaСодержание книги
Поиск на нашем сайте
Раніше усі наші маніпулювання із wp базувалися на тому, що ми вважали відомим, як саме виконуються всі команди програми S. Наразі ми змінимо концепцію. Будемо вважати первинним предикат wp і умови, яким він задовольняє. Це дозволить нам визначити в термінах wp всі команди мови, а потім доводити різні твердження про програми. Природно першим розглянемо пустий оператор.
Визначення 9.5.
Визначення 9.6.
Виконання виклику вказаного методу приводить до термінового завершення виконання програми. Тому очевидним бачиться висновок, що за довільного початкового стану після цього виклику методу предикат R буде хибним.
Визначення 9.7. (послідовне виконання)
Зрозуміло, що у випадку більшої кількості послідовного виконання, цим визначенням можна скористатися потрібним числом повторень. Більш змістовним бачиться визначення оператору присвоєння. Спочатку розглянемо присвоєння простої змінної. Визначення 9.8.
де domain(e) – предикат, який описує множину всіх станів, у яких може бути обчислене е (тобто де воно визначене), а Наприклад:
У випадку присвоєння елемента масива потрібно враховувати можливість виходу індексу за межи масиву. Введемо до розгляду предикат inrange(b,i), який буде визначати множину допустимих значень індексу і у масиві b. Тоді: Визначення 9.9 Для присвоєння елементу масиву найслабкіша передумовавизначатиметься так:
Наприклад. Нехай м аємо масив b[0..9] і обчислимо найслабшу передумову:
Оператор if і найслабша передумова Відмітимо, що короткий if еквівалентний повному з пустим оператором в else частині, а оператор switch також може бути визначений декількома операторами if-else. Тому всі конструкції вибору мови Java можуть бути виражені через конструкцію «if (e) S1; else S2;». Визначення 9.10. wp("if (e) S1; else S2;",R) = domain(e)&& (e ⇒ wp("S1;",R)) ∧ (!e ⇒ wp("S2;",R)).
У якості прикладу використання цього визначення переконаємося втому, що wp("if (x >= y) z=x; else z=y;", z = max(x, y)) = T.
Дійсно, wp("if (x >= y) z=x; else z=y;", z = max(x, y)) =
Покажемо, що кожний із двох членів отриманої кон’юнкції є тавтологією. Розглянемо, наприклад, перший із них: ((x <y) ∨ (x = max(x, y)).Якщо x < y, тоді перший член дизюнкції – істинний.
В іншому випадку x > y і тому буде істинним її другий член, що і доводить потрібне. Аналогічні роздуми можна провести і для виразу (x ≥ y) ∨ (y = max(x, y))), що і завершує доведення. Для практичного застосування найчастіше потрібне не обчислення найслабшої передумови, а лише перевірка того факта, що деяка інша передумова забезпечує її виконання. Тому буде корисною наступна теорема.
Теорема 9.1. Нехай предикат Q задовольняє умові ((Q ∧ e) ⇒ wp(S1,R)) ∧ ((Q∧!e) ⇒ wp(S2,R)). Тоді (і тільки тоді) Q ⇒ wp("if (e) S1; else S2;",R).
Доведення. ((Q ∧ e) ⇒ wp(S1,R)) = (!(Q ∧ e) V wp(S1,R)) = (!Q V!e V wp(S1,R)) = (!Q V (e ⇒ wp(S1,R))) = (Q ⇒ (e ⇒ wp(S1,R))).
Аналогічно отримаємо ((Q∧!e) ⇒ wp(S2,R)) = (Q ⇒ (!e ⇒ wp(S2,R))), і, тому, (((Q ∧ e) ⇒ wp(S1,R)) ∧ ((Q∧!e) ⇒wp(S2,R))) = ((Q ⇒ (e ⇒ wp(S1,R))) ∧ (Q ⇒ (!e ⇒ wp(S2,R)))) = (Q ⇒ ((e ⇒ wp(S1,R)) ∧ (!e ⇒ wp(S2,R)))) = (Q ⇒ wp("if (e) S1; else S2;",R)).
Цикли в термінах wp. У термінах найслабшої передумови можна визначити і всі інші конструкції мови. Та ми обмежимся лише визначенням циклу while. Справа в тім, що навіть воно залишається безглуздим на практиці, але все ж дає декілька конструктивних підходів побудови циклів (інваріант циклу). Для визначення найслабшої передумови wp("while(e)S;",R скористаємося додатковими визначеннями:
Визначення 9.11. H0(R) = domain(e)&&(!e∧R), Hk(R) = Hk−1(R) V (domain(e)&&wp(S,Hk−1(R))), де предикат Hk(R) описує множину усіх станів, у яких виконання циклу "while(e)S;" закінчується не більше, ніж за k ітерацій, у стані, що задовольняє R.
Тоді основне визначення прийме вигляд.
Визначення 9.12. wp("while(e)S;",R) = (∃k ≥ 0 Hk(R)).
Для циклу "while (i<1) i=i+1;" і післяумови R = (i = 1) маємо H0(R) = (i > 1 ∧ i = 1) = (i = 1).
Тобто, за такої передумови виконання циклу завершиться за нуль ітерацій і дасть результат R. Потім, легко порахувати
wp("i=i+1;", H0(R)) = (i + 1 = 1) = (i = 0) і
і т.д.
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.18 (0.007 с.) |

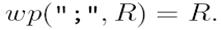
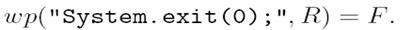

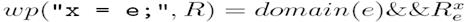
 позначає підстановку в предикат R виразу е замість усіх вільних входжень змінної х.
позначає підстановку в предикат R виразу е замість усіх вільних входжень змінної х.

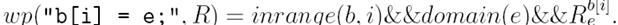


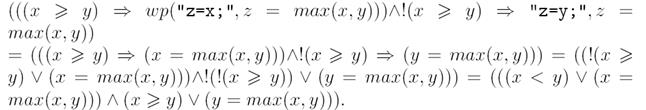
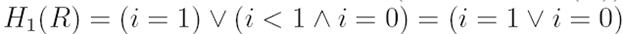 Аналогічно знаходимо
Аналогічно знаходимо



