
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основи оцінок складності алгоритмівСодержание книги
Поиск на нашем сайте Нам вже відомо що правильність – далеко не єдина якість, яку повинна мати гарна програма. Однією з найважливіших є ефективність, що характеризує передусім час виконання програми T (n) для різних вхідних даних (параметра n). Знаходження точної залежності T (n)для конкретної програми – завдання досить складне. З цієї причини зазвичай обмежуються асимптотичними оцінками цієї функції, тобто описом її зразкової поведінки при великих значеннях параметра n. Іноді для асимптотичних оцінок використовують традиційне відношення O (читається <<О велике>>) між двома функціями В якості першого прикладу повернемося до тільки що розглянутих програм знаходження факторіалу числа. Легко бачити що кількість операцій, які мають бути виконані для знаходження факторіалу У подібній ситуації прийнято говорити що програма (чи алгоритм) має лінійну складність (складність Чи можна обчислити факторіал швидше? Виявляється, так. Можна написати таку програму, яка даватиме правильний результат для тих же значень Не менш цікавий і приклад рекурсивного обчислення
ЗАВДАННЯ 8.1. Напишіть програму, що друкує n -е число Фібоначчі, яка мала б лінійну складність. Ось розв’язання цієї задачі, в якій змінні j і k містять значення двох послідовних чисел Фібоначчі. Текст програми: public class FibIv1 { public static void main(String[] args) throws Exception { int n = Xterm.inputInt("Введите n -> "); Xterm.print("f(" + n + ")"); if (n < 0) { Xterm.print("не визначено\n"); } else if (n < 2) { Xterm.println(" = " + n); } else { long i = 0; long j = 1; long k; int m = n; while (–m > 0) { k = j; j += i; i = k; } Xterm.println(" = " + j); } }} Наступне питання цілком природне – а чи можна знаходити числа Фібоначчі ще швидше? Після вивчення певних розділів математики зовсім просто вивести наступну формулу для -
Може здатися, що грунтуючись на ній, легко написати програму із складністю Текст програми: public class FibIv2 { public static void main(String[] args) throws Exception { int n = Xterm.inputInt("Введите n -> "); double f = (1.0 + Math.sqrt(5.)) / 2.0; int j = (int)(Math.pow(f,n) / Math.sqrt(5.) + 0.5); Xterm.println("f(" + n + ") = " + j); }} Насправді ця програма використовує виклик функції піднесення до степеня Math.pow(f, n), яка не може бути реалізована швидше, ніж за логарифмічний час ( Для обчислення
ЗАВДАННЯ 8.2. Напишіть програму, що виводить n-е число Фібоначчі, яка мала б логарифмічну складність. Текст програми: public class FibIv3 { public static void main(String[] args) throws Exception { int n = Xterm.inputInt("Введите n -> "); Xterm.print("f(" + n + ")"); if (n < 0) { Xterm.println(" не определено"); } else if (n < 2) { Xterm.println(" = " + n); } else { Matrix b = new Matrix(1, 0, 0, 1); Matrix c = new Matrix(1, 1, 1, 0); while (n>0) { if ((n&1) == 0) { n >>>= 1; c.square(); } else { n -= 1; b.mul(c); } } Xterm.println(" = " + b.fib()); } }}class Matrix { private long a, b, c, d; public Matrix(long a, long b, long c, long d) { this.a = a; this.b = b; this.c = c; this.d = d; } public void mul(Matrix m) { long a1 = a*m.a+b*m.c; long b1 = a*m.b+b*m.d; long c1 = c*m.a+d*m.c; long d1 = c*m.b+d*m.d; a = a1; b = b1; c = c1; d = d1; } public void square() { mul(this); } public long fib() { return b; }} Якщо спробувати порахувати десятимільйонне число Фібоначчі за допомогою цієї і попередньою програм, то різниця в часі обчислень буде цілком очевидною. На жаль, результат буде хибним (у обох випадках) через обмеженість діапазону чисел типу long. На закінчення приведемо порівняльну таблицю часів виконання алгоритмів з різною складністю і пояснимо, чому зі збільшенням швидкодії комп'ютерів важливість використання швидких алгоритмів значно зростає. Розглянемо чотири алгоритми розв’язку однієї і тієї ж задачі, складності
Коли програмісти-початківці тестують свої програми, то значення параметрів, від яких вони залежать, зазвичай невеликі. Тому навіть якщо при написанні програми був застосований неефективний алгоритм, це може залишитися непоміченим. Проте якщо подібну програму спробувати застосувати в реальних умовах, то її практична непридатність проявиться негайно. Зі збільшенням швидкодії комп'ютерів зростають і значення параметрів для яких робота того або іншого алгоритму завершується за допустимий час. Таким чином, збільшується середнє значення величини
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 , визначення якого можна знайти у будь-якому підручнику по математичному аналізу, хоча частіше застосовують відношення еквівалентності (читається <<тета велике>>). Його формальне визначення є, наприклад, в книзі [Глибовець], хоча нам поки що досить буде розуміння цього питання у загальних рисах.
, визначення якого можна знайти у будь-якому підручнику по математичному аналізу, хоча частіше застосовують відношення еквівалентності (читається <<тета велике>>). Його формальне визначення є, наприклад, в книзі [Глибовець], хоча нам поки що досить буде розуміння цього питання у загальних рисах. числа
числа  в першому наближенні прямо пропорційно цьому числу, бо кількість повторень циклу (ітерацій) в цій програмі рівна
в першому наближенні прямо пропорційно цьому числу, бо кількість повторень циклу (ітерацій) в цій програмі рівна  .
. або
або  ).
). , що фактично означає організацію обчислень за деякою формулою без застосування циклів і рекурсивних викликів!
, що фактично означає організацію обчислень за деякою формулою без застосування циклів і рекурсивних викликів! ,. Подібні програми практично не застосовуються на практиці. У цьому дуже легко переконатися спробувавши вирахувати з її допомогою 40-е число Фібоначчі. З цієї причини цілком актуальне наступне завдання.
,. Подібні програми практично не застосовуються на практиці. У цьому дуже легко переконатися спробувавши вирахувати з її допомогою 40-е число Фібоначчі. З цієї причини цілком актуальне наступне завдання. , яку легко перевірити для невеликих значень
, яку легко перевірити для невеликих значень 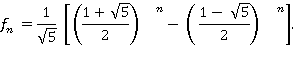
 , що не використовує ітерації або рекурсії.
, що не використовує ітерації або рекурсії. ). Про алгоритми у яких кількість операцій приблизно пропорційно
). Про алгоритми у яких кількість операцій приблизно пропорційно  -го числа Фібоначчі існує такий алгоритм програмну реалізацію якого ми приведемо без додаткових коментарів, – інакше треба пояснювати надто багато (зв'язок чисел Фібоначчі з мірами матриці порядку два, використання класів для роботи з матрицями, алгоритм швидкого зведення матриці в степінь).
-го числа Фібоначчі існує такий алгоритм програмну реалізацію якого ми приведемо без додаткових коментарів, – інакше треба пояснювати надто багато (зв'язок чисел Фібоначчі з мірами матриці порядку два, використання класів для роботи з матрицями, алгоритм швидкого зведення матриці в степінь). ,
, 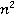 і
і  відповідно. Припустимо, що другий з цих алгоритмів вимагає для свого виконання на деякому комп'ютері при значенні параметра
відповідно. Припустимо, що другий з цих алгоритмів вимагає для свого виконання на деякому комп'ютері при значенні параметра  рівно одну хвилину часу. Тоді час виконання усіх цих чотирьох алгоритмів на тому ж комп'ютері при різних значеннях параметра будуть приблизно такими, як в таблиці 8.1.
рівно одну хвилину часу. Тоді час виконання усіх цих чотирьох алгоритмів на тому ж комп'ютері при різних значеннях параметра будуть приблизно такими, як в таблиці 8.1.


 сек.
сек.
 сек.
сек.
 сек.
сек.
 хв.
хв.
 год.
год.
 сек.
сек.
 років
років
 хв.
хв.
 років
років
 років
років
 , і, отже, зростає величина відношення часів виконання швидкого і повільного алгоритмів. Чим швидше комп'ютер тим більше відносний програш при використанні поганого алгоритму!
, і, отже, зростає величина відношення часів виконання швидкого і повільного алгоритмів. Чим швидше комп'ютер тим більше відносний програш при використанні поганого алгоритму!


