
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектування рекурсії та ітераціїСодержание книги
Поиск на нашем сайте
Як визначення цих двох базисних схем обробки інформації, так і їх взаємозв'язок вже були розглянуті нами раніше. Нагадаємо найголовніше.
Рекурсія - це такий спосіб організації обробки даних, за якого програма викликає сама себе безпосередньо, або за допомогою інших програм.
Продовжимо дослідження застосування рекурсії, звертаючи особливу увагу на процес побудови програми і доведення її правильності. Рекурсивна програма зазвичай виникає, як результат рекурсивного обчислення певної функції на множині програмних змінних, а доведення її правильності вимагає дослідження двох питань: Розглянемо таку задачу.
Розв’язок. Фіксуючи a, розглянемо функцію
Програма, яка вичисляє функцію Текст програми: public class MulR { static int mul(int x, int y) { // Xterm.print(" Вызов mul(" + x + "," + y + ")\n"); return (y == 0)? 0: ((y&1) == 0)? mul(x,y >>> 1) << 1: mul(x,y-1) + x; } public static void main(String[] args) throws Exception { int a = Xterm.inputInt("a -> "); int b = Xterm.inputInt("b -> "); Xterm.println("a * b = " + mul(a,b)); }}
Доведення правильності одержуваного результату проведемо за допомогою методу математичної індукції, показавши, що при фіксованому a та 0 Справедливість бази індукції Нехай спочатку число Якщо число Обгрунтування цих рівностей проводиться аналогічно. Таким чином, нами перевірена істинність індуктивного переходу Для того щоб побачити ланцюжок рекурсивних викликів функції Кожен рекурсивний виклик функції В якості додаткового завдання можете спробувати пояснити ті результати, які виходять при виконанні цієї програми для від'ємних значень
ЗАВДАННЯ 9.23. Напишіть програму, яка друкує значення багаточлена степеню
Рішення. Зауважимо, що
Скориставшись цим, визначимо функцію
Тепер можна написати програму, яка реалізовує обчислення цієї функції.
Текст програми: public class PolVal { static int a[], x0; static int pol(int k) { return (k == 0)? a[0]: x0 * pol(k-1) + a[k]; } public static void main(String[] args) throws Exception { int n = Xterm.inputInt("n -> "); a = new int[n+1]; for (int i=0; i<=n; i++) a[i] = Xterm.inputInt("a[" + i + "] -> "); x0 = Xterm.inputInt("x0 -> "); Xterm.println("P(" + x0 + ") = " + pol(n)); }}Завершення програми за кінцеве число кроків випливає із зменшення на одиницю при кожному рекурсивному виклику аргументу функції
База індукції перевіряється безпосередньо, бо при нульовому значенні аргументу функція Рекурсивне рішення задачі часто є менш ефективним, ніж еквівалентна йому за іншими параметрами ітераційне рішення. Звичайним способом програмної реалізації ітерації є цикл, і тому ми будемо вважати, що специфікація завдання на ітерацію має вигляд {Q} "S0; while (e) S;" {R}.
.
Розглянемо X - множину значень всіх програмних змінних (прямий добуток множин значень окремих змінних), його підмножини Тоді побудова умови продовження циклу e і його тіла S зводиться до знаходження предиката e і такого перетворення, що Саме цей факт є основним результатом, що випливає з визначення найслабшої передумови wp для оператора циклу. Геометрична інтерпретація математичної моделі ітерації, що зводиться до багаторазового застосування перетворення T, наведена на рисунку 9.1. На жаль ця математична модель ітерації є занадто загальною і важко застосовною на практиці, так як вона не дає конкретних рекомендацій по знаходженню умови продовження циклу
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.149.164 (0.01 с.) |


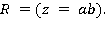 Числа
Числа  програмі змінювати не можна. Часова складність програми не повинна перевершувати
програмі змінювати не можна. Часова складність програми не повинна перевершувати 
 , яка задається наступним рекурсивним визначенням:
, яка задається наступним рекурсивним визначенням: ,
,  , коли b позитивно і парне,
, коли b позитивно і парне, , коли b позитивно і парне.
, коли b позитивно і парне. , легко пишетья у відповідності з її виразом. У цілях ефективності ділення навпіл та множення на два реалізується за допомогою зсувів.
, легко пишетья у відповідності з її виразом. У цілях ефективності ділення навпіл та множення на два реалізується за допомогою зсувів. може бути довільною.
може бути довільною. є тавтологією предикат
є тавтологією предикат  = (дана програма друкує
= (дана програма друкує  ).
). випливає безпосередньо з тексту програми, а індуктивний перехід
випливає безпосередньо з тексту програми, а індуктивний перехід 
 здійснюється наступним чином. Якщо припустити, що програма правильна при
здійснюється наступним чином. Якщо припустити, що програма правильна при  , то
, то  . Розглянемо далі два можливих випадки.
. Розглянемо далі два можливих випадки. - парне. Тоді результатом роботи програми буде
- парне. Тоді результатом роботи програми буде 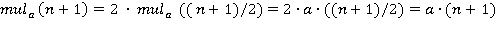 . Перша рівність тут випливає з тексту програми, а друга - з припущення індукції.
. Перша рівність тут випливає з тексту програми, а друга - з припущення індукції. .
. , що і закінчує доведення.
, що і закінчує доведення. досить прибрати символи коментаря з першого рядка цього методу. Це дозволяє зрозуміти, чому програма має складність порядку
досить прибрати символи коментаря з першого рядка цього методу. Це дозволяє зрозуміти, чому програма має складність порядку  . Доведемо акуратно, що глибина рекурсії (кількість рекурсивних викликів) для нашої програми не перевершує
. Доведемо акуратно, що глибина рекурсії (кількість рекурсивних викликів) для нашої програми не перевершує  (тут
(тут  - ціла частина від
- ціла частина від  ).
). зменшує значення аргументу
зменшує значення аргументу  або на одиницю, або вдвічі. Два послідовних виклику цієї функції завжди приводять до зменшення величини
або на одиницю, або вдвічі. Два послідовних виклику цієї функції завжди приводять до зменшення величини  рекурсивних викликів. Зверніть увагу, що ми не враховуємо в наших міркуваннях найперший, нерекурсивний виклик функції
рекурсивних викликів. Зверніть увагу, що ми не враховуємо в наших міркуваннях найперший, нерекурсивний виклик функції  .
.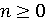 в заданій точці
в заданій точці  . Коефіцієнти багаточлена зберігаються в масиві
. Коефіцієнти багаточлена зберігаються в масиві  за порядком зменшення ступенів і є цілими числами, також як і значення
за порядком зменшення ступенів і є цілими числами, також як і значення  , де
, де ,
, наступним чином:
наступним чином: ,
,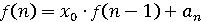 , при
, при  .
. , а її правильність виходить з доказу по індукції наступного твердження
, а її правильність виходить з доказу по індукції наступного твердження  (програма друкує значення
(програма друкує значення  багаточлена
багаточлена  ступеня n в точці
ступеня n в точці  повертає
повертає  , що збігається з
, що збігається з  . Індуктивний перехід вдається здійснити завдяки формулі, наведеної на початку вирішення даної задачі, що дозволяє виразити значення
. Індуктивний перехід вдається здійснити завдяки формулі, наведеної на початку вирішення даної задачі, що дозволяє виразити значення  через
через  .
.
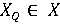 і
і  , зумовлені предикатами Q і R, і перетворення T: X → X, відповідне разовому виконанню тіла циклу S.
, зумовлені предикатами Q і R, і перетворення T: X → X, відповідне разовому виконанню тіла циклу S.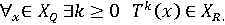
 і тіла циклу S за заданими Q і R. До розгляду більш часткових і більше корисних схем ми зараз і перейдемо.
і тіла циклу S за заданими Q і R. До розгляду більш часткових і більше корисних схем ми зараз і перейдемо.


