
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Об’єктно-орієнтовне програмуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Об’єктно-орієнтована парадигма наділила класи ієрархією. Об’єктно-орієнтоване програмування за метафорою Б.Страуструпа, автора С++ (однієї з найпопулярніших мов об’єктно-орієнтованого програмування), — це високоінтелектуальний синонім доброго програмування. Дійсно, нові парадигми програмування з’являються не так часто, не частіше однієї в десятиліття. Той факт, що об’єктно-орієнтована парадигма успішно використовується протягом 20 років, сам по собі служить вагомим підтвердженням її життєздатності. Дійсно, алгоритми, реалізовані в процедурному програмуванні, надто конкретні. Будь-яка модифікація — це вже новий алгоритм і таким чином кількість процедур і функцій, що знаходяться у вжитку, надмірно зростає. Модульне програмування групує алгоритми в модулі, одночасно інкапсулюючи структури даних. Тепер залишається зробити наступний крок — побудувати ієрархію модулів або класів. Таких ієрархій може бути дві. Перша з них — бути частиною чогось. Наприклад, грань є частиною багатогранника, ребро — частиною грані, вершина — частиною ребра. Інша ієрархія — бути узагальненням або конкретизацією. Наприклад, овал і многокутник служать конкретизацією плоскої фігури, коло — конкретизацією овалу, чотирикутник — конкретизацією многокутника, подальшими конкретизаціями чотирикутника можуть служити паралелограм, прямокутник, ромб, квадрат. Той факт, що квадрат, ромб, прямокутник є повноцінними паралелограмами дозволяє їм користуватися усіма програмними засобами, створеними для паралелограма, паралелограм в свою чергу є повноцінним чотирикутником і так далі. Цей принцип, відомий під назвою reusable — знову вживаний — став одним з найважливіших досягнень об’єктно-орієнтованої парадигми. Знову вживаючи вже існуюче програмне забезпечення в більш конкретизованих умовах, ми дописуємо лише ту його частину, яка стосується особливостей наявної конкретизації. Цей принцип дістав назву programming by difference або дописування програм. І, нарешті, об’єктно-орієнтована парадигма доводить до логічної завершеності принцип моделювання реального світу, а точніше тієї його частини, абстракцією якої служить програма. При цьому підході програма складається з об’єктів, що відповідають реальним поняттям або предметам. Виконання програми зводиться до взаємодії об’єктів, яке служить абстракцією реальної взаємодії їх прототипів. Все це разом забезпечило об’єктно-орієнтованому підходу беззаперечне лідерство в галузі розробки програм. Сьогодні в сімействі мов об’єктно-орієнтованого програмування три найбільш відомих представника: С++, Java і C# (читається Сі шарп). С++ і сьогодні залишається визнаним лідерів в розробці великих і складних програмних систем. Java і C# виросли з С++. Вони мають свою сферу застосування в розподіленому програмуванні і будуть вивчатися нами пізніше. Ще одна перевага С++ — його мультипарадигменність. С++ містить в собі мову С (з деякими застереженнями), а тому, природно, підтримує процедурну парадигму. Ось приклад функції для обчислення квадратного кореня в С/С++: double root (double x, double eps) { double s=0.5*x; double t; do { t=s; s=(s+x/s)*0.5; } while ((fabs(s-t)/s)>eps); return s; }; С++ також підтримує традиційні для модульного програмування механізми абстракції даних, доповнені можливостями об’єктно-орієнтованої парадигми. Ось якого виду набуде наведений вище приклад із Модули 2 enum month {jan=1, feb, mch, apr, may, jun, jul, aug, sep, oct, nov, dec}; struct Month {inline int length(){return len[mon-1];} Month(month n):mon(n){}; private: month mon; static int len[12]; };
int Month::len[12] {31,28,31,30,31,30,31,31,30,31,30,31};
Тепер Month — це повноцінний тип даних, який можна вживати, нарівні зі стандартними, у визначенні змінних, наприклад, Month theMonth = may; int i = theMonth.length();
Як ми побачимо далі, можна навіть довизначити арифметичні операції, наприклад, операцію збільшення місяця на ціле число, що дозволить писати вирази виду theMonth + 5. І, нарешті, С++ реалізує парадигму узагальнених функцій і параметризованих типів, але про це далі. Функціональне програмування Функціональний стиль програмування оснований на використанні тільки процедур-функцій. Роль змінних виконують параметри функцій. Присвоєння значень проходить тільки при визначенні (заданні) аргументів при звертанні до функцій. Послідовна композиція операторів замінюється покроковим обчисленням аргументів при виклику функції, умовна композиція операторів – такою ж композицією виразів, циклічна композиція – рекурсією. Подумайте про архітектурні концепції розглянутих нами типів обчислювачів та їх можливості по реалізації функціонального стилю!!!!! Може здатися, що арсенал таких засобів програмування досить бідний. Але це далеко не так! Програми, написані функціональною мовою програмування (ФМП), традиційно є коротшими, нагляднішими і простішими для розуміння. До того ж вони є і надійнішими – «змінна» (новий екземпляр параметра функції) створюється тільки в момент присвоєння їй значення і не змінює його за весь час свого існування. Використання рекурсії при виклику функції добре співвідноситься з рекурсивним стилем опису типів значень і таких конструкцій, як виразів, зокрема – звернення до функції (вираз будується за допомогою композиції звертань до функцій-операцій). В якості прикладу ФМП приведемо лісповське визначення рекурсивної функції append, яка вставляє в початок списку У (її другого параметру) всі елементи списку Х, зберігаючи їх порядок: (define append (lambda (X Y) (cond ((NULL X) Y) (T (cons (car X) (append (cdr X) Y)) ) ) ) ) Узагальнимо приведені рішення для функціональної парадигми Дані тут представляються як функціональні вирази, а алгоритми - як системи функціональних рівнянь. Кожній програмі відповідає часткова функція чи множина функцій, що складають найменший розв’язок канонічної системи функціональних рівнянь, тобто системи вигляду
де х = ( Існує велика кількість функціональних мов програмування, починаючи з мови LISP та її нащадків і до сучасних мов, таких як SHEMA і ML. Для функціональних програм існує значно більше стратегій обчислень, ніж для процедурних. Добре відомі відмінності між такими стратегіями як “виклик за іменем” і “виклик за значенням”, паралельна і послідовна підстановки і іншими, що використовуються при виконанні функціональних програм. Але у всіх випадках елементарним кроком обчислень є підстановка функціонального означення і спрощення виразів. До того ж, як тільки обчислення закінчуються, то результат визначений однозначно. Іншими словами, стратегія лише визначає час, необхідний на обчислення, і як ці обчислення проводяться, але не остаточний результат.
Абстрактна семантика функціональних програм. Якщо
де х = ( Денотаційна семантика. Нехай D, як і раніше, є область даних для змінних програм. Тоді
Приклад 3.1. Нехай програма Р маг вигляд
F(x, у) = if х = у then у + 1 else F(х, F(x -1, у + 1)). Функції
де ┴ - символ невизначеності, є розв’язком програми-рівняння Р. Це означає, що коли всі входження функції F в програмі замінити на функцію f і, i = 1,2,3, то зліва і справа від знака рівності будуть стояти однакові функції, тобто
Дійсно, розглянемо, наприклад, функцію
Розглянемо два випадки: a) х-1 = у+1 b) х – 1 ≠ у + 1 В обох випадках отримуємо
then
Отже, остаточно одержуємо
Перевірку того, що решта функцій теж є нерухомими точками програми Р пропонується виконати як корисну вправу. Будемо говорити, що функції Таким чином, всі три функції є розв’язком функціонального рівняння, яке визначає програму Р, і виникає питання: а яку з цих функцій потрібно розглядати як результат виконання програми Р? Якщо порівнювати між собою функції В цьому випадку говорять, що функція
Неважко переконатися в тому, що відношення Можна показати, що розглянута вище функція
Розширимо відношення
f = ( Найбільш важливою властивістю функціональних програм є властивість, яку висвітлює відома теорема Кліпі [15]. Теорема 3.2. Будь-яка функціональна програма Р має єдину найменшу нерухому точку Операційна семантика. Нехай Р = F(f,x) = Е - функціональна програма. Вираз
Е[ означає одночасну підстановку в функціональний вираз Е замість змінних Е = F(x, у) і Е[х:= 1, у:= 2] = if (1 = 2) then 2 + 1 else F(1, F(1 -1,2 + 1)).
Якщо одержаний вираз спростити, то
Е[х:= 1,у:= 2] = F(1,F(0,3)).
Позначимо функцію спрощення функціональних виразів через simp. Станом обчислень функціональної програми називається функціональний вираз, а відношення переходів на функціональних виразах задається за допомогою такого правила:
Приклад 3.2. Якщо F(x,y) - функція з попереднього прикладу, то F(3,1) оскільки F(3, F(2,2)) = if (3 = F(2,2)) thеп 4 else F(2, F(2,2) + 1 )); F(2,2) = if (2 = 2) then(2+1) elseF(2, F(1, 3)) = (2 + 1) = 3. Тоді F(3,F(2,2)) = 4.
Як випливає з наведених прикладів, значенням функціональної програми Р є або константний вираз А, тобто деякий елемент області даних D, одержаний в результаті спрощення (наприклад, А — 4 в розглянутому вище прикладі), або невизначений елемент ┴. Зв’язок між денотаційною і операційною семантикою встановлює таке твердження.
Теорема 3.3. Нехай Доведення пропонується як вправа. Нижче наводиться функціональна програма обчислення НСД двох натуральних чисел. НСД(x,y) = if (х > у) then НСД(х - у, у) else if (х < у) then НСД(x, у - х) else х. Функціональні програми мають одну дуже корисну властивість порівняно з процедурними програмами: функціональні програми не мають побічних ефектів, пов’язаних з використанням глобальних змінних, в той час як процедурні програми схильні до такого роду ефектів. Побічні ефекти часто приводили до того, що великі затратні розробки зазнавали краху, тому що помилки, які виникають з цих причин, не мають стійкого характеру (їх називають “мерехтливими” помилками). Ці помилки проявляються не завжди при роботі програми і тому їх дуже важко ідентифікувати і виправити. Розглянемо програму (мова програмування - ПАСКАЛЬ), яка має побічний ефект. Наведена нижче програма обчислює значення суми f(1) + f(2), де f - деяка процедура-функція.
program example(output); var flag: bool; function f(n: integer): integer; Begin if flag then f:= n else f:= 2n; flag:= not flag end;
Begin flag:= true; writeln (f(1) + f(2)); writeln (/(2) + /(1)) end;
Результат роботи програми буде для першого виразу 5, а для другого виразу - 4. Оскільки операція додавання комутативна в множині натуральних чисел, то результати повинні були б збігатися. Причина криється в змінній flag, яка є глобальною і змінює значення функції f.
Логічне програмування Для представлення даних використовуються терми і предикатні терми. Алгоритми представляються за допомогою аксіом і правил виведення. Елементарним кроком обчислень є уніфікація і підстановка. Об’єкт, що співставляється логічній програмі, являє собою семантичну модель логічної системи, яку можна також розглядати як опис відповідної предметної області. Вхідні дані представляються за допомогою мови запитів. Кожний запит можна розглядати як систему логічних (алгебраїчних, якщо предикат рівності є одним із предикатів) рівнянь, а стратегія є стратегією пошуку розв’язків цих рівнянь. Стратегія для логічної мови визначає побудову дерева пошуку виведення. Для цієї парадигми існує набагато більше свободи при виборі способу розв’язку задач, ніж для інших парадигм, і тому практика логічного програмування породила цілий ряд спеціальних засобів для управління стратегіями. Як правило, ці засоби включаються в мову (наприклад, різні види оператора відтинання (cut-оператор)). Логічна програма обчислення НСД. Для побудови логічної програми представимо бінарну функцію НСД у вигляді тернарного предиката НСД, який визначається таким чипом: НСД1 (x,y,z) = 1 ⇔ НСД(x, у) = z.
НСД1 (x,y,z). Begin 1) НСД1(х,x,x); 2) НСД1(х,y, z): -(х > у)& НСД1(x -y,y,z) 3) НСД1(x, у, z): - (х < у)& НСД1(x, у - x, z) 4) НСД1( End
Однією із мов логічного програмування є Пролог. При побудові програм Прологу використовується той же підхід, що й у предикативних логіках. Для опису предметної області ми трансформуємо речення природної мови, ставлячи на перше місце відношення. Наприклад: · Японський автомобіль економний. -> економний(японський_автомобіль), · Вані подобається автомобіль, якщо він економний. -> подобається (ваня,автомобіль) іf економний(автомобіль). Програміст визначає об’єкти і відношення. Потім формулює правила про те, у якому разі ці відношення справджуються. Правило, що визначає, коли речення Вані подобається автомобіль справджується, матиме вигляд: Вані подобається автомобіль, якщо він економний. У Пролозі зв’язок між об’єктом називається фактом. Факти можуть виражати як властивості, так і відношення: економний (автомобіль), студент (Ваня). Правила визначають які висновки можна зробити з даних правил. Ми можемо задавати питання про пролог відношення у вигляді запитів. Пролог-система будує відповідь і виводить її до друку. Наприклад, речення Що подобається Вані? Трансформується у запит подобається (ваня,Що). Правила Прологу складаються з трьох частин: голови, символу і тіла. Наприклад, у правилі can_buy(X, Y):- Person(X), Car(Y), Likes(X, Y), for_sale(Y). can_buy(X, Y)- голова, :- символ, person(X), car(Y), likes(X, Y), for_sale(Y) -тіло.
Розглянемо програму:
Predicates can_buy(symbol, symbol) person(symbol) car(symbol) Likes(symbol, symbol) for_sale(symbol ) Clauses can_buy(X, Y):- Person(X), Car(Y), Likes(X, Y), for_sale(Y). Person(kelly). Person(judy). Car(lemon). car(hot_rod). likes(kelly, hot_rod). likes(judy, pizza). for_sale(pizza). for_sale(lemon). for_sale(hot_rod).
До програми можна задати питання: Що можуть купити judy i kelly? can_buy(judi,X) & can_buy(kelly,X). Хто може купити бутерброд з гарячою сосискою? can_buy(X,hot_rod).
Розглянемо ще одну програму в PDC Prolog.
Predicates likes(symbol,symbol) Clauses likes(ellen, reading). Likes(john, computers). Likes(john, badminton). Likes(leonard, badminton). Likes(eric, swimming). Likes(eric, reading).
Побудуємо запит: Чи існує особа, яка любить читати і купатися? likes(Person,reading) and likes(Person,swimming) Відповіддю буде: Person = eric Solution
Алгебраїчна парадигма Дані представляються за допомогою термів або позначених графів, а алгоритми - системами правил переписування (орієнтованих рівностей чи умовних рівностей, співвідношень алгебри даних). Об’єкт, який визначається системою рівностей, за допомогою яких виражаються правила переписування, є відношенням конгруентності на множині всіх термів абсолютно вільної алгебри термів, що породжується константами. Це відношення визначається як конгруентне замикання співвідношень переписування, які розглядаються як тотожності алгебри термів. Елементарним кроком обчислень в алгебраїчній парадигмі є мeтчінг (відповідність зразку), перевірка умов і підстановка. Стратегія переписування визначає, в якому порядку застосовуються правила переписування і підтерми (підвирази) поточного терма для співставлення з лівими частинами співвідношень. Для канонічних систем правил переписування результат не залежить від стратегії. Якщо система правил не є канонічною, то стратегія визначає не тільки час переписування, але й результат. В будь-якому випадку результат переписування, за умови закінчення обчислень, є термом, який еквівалентний висхідному термові за відношенням конгруентності, що визначається системою правил переписування. Тобто, стратегія вибирає результат в класі конгруентних термін. Відповідна алгебраїчна програма обчислення НСД наведена нижче.
RS(х,у) ( (x, х) = x, (х > у) (x < у) ).
Висновок Завершуючи вступ і короткий історичний екскурс, зазначимо, що роботи останніх років в області інтелектуалізації мов програмування показують тенденцію до інтеграції розглянутих вище парадигм. Ідеалом методології програмування є принцип: простий алгоритм для ефективного розв’язання складної задачі. Існує багато шляхів для досягнення цієї мети, один з яких можна виразити формулою
алгоритм = означення + стратегія обчислень, яку можна доповнити відомою формулою Вірта
програма = алгоритм + структури даних.
Лекція 4.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 (x) =
(x) =  (f,x),i= 1,2,...,m,
(f,x),i= 1,2,...,m, ),f = (
),f = ( 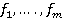 ).
). D. Слід зазначити, що коли у функціональному рівнянні розглядати лише повністю визначені функції, то розв’язку може й не існувати. Якщо ж припустити, що функції
D. Слід зазначити, що коли у функціональному рівнянні розглядати лише повністю визначені функції, то розв’язку може й не існувати. Якщо ж припустити, що функції  часткові, то розв’язок існує завжди, але цей розв’язок може бути не єдиний.
часткові, то розв’язок існує завжди, але цей розв’язок може бути не єдиний. (x, у) = if х = у then у + 1 else x + 1;
(x, у) = if х = у then у + 1 else x + 1;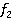 (х, у) = if х ≥ 1 then х + 1 else у - 1;
(х, у) = if х ≥ 1 then х + 1 else у - 1;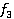 (x, у) = if x ≥ у & ((x - y)mod 2 = 0) then у + 1 else ┴,
(x, у) = if x ≥ у & ((x - y)mod 2 = 0) then у + 1 else ┴,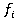 (x - 1,у + 1)).
(x - 1,у + 1)). (x - 1 ,у+ 1));
(x - 1 ,у+ 1));
 = 1,2,3, - це нерухомі точки функціональної програми Р.
= 1,2,3, - це нерухомі точки функціональної програми Р. то виявляється, що коли визначена функція
то виявляється, що коли визначена функція  але не навпаки.
але не навпаки. і позначають це так:
і позначають це так: .
. є відношенням часткового порядку і, отже, можна говорити, зокрема, про мінімальні і найменші елементи на множині функцій відносно цього порядку.
є відношенням часткового порядку і, отже, можна говорити, зокрема, про мінімальні і найменші елементи на множині функцій відносно цього порядку. відносно даного порядку менша не тільки по відношенню до функцій
відносно даного порядку менша не тільки по відношенню до функцій  а й по відношенню до будь-якої нерухомої точки програми Р. Більше того, можна показати, що
а й по відношенню до будь-якої нерухомої точки програми Р. Більше того, можна показати, що  )
)  ) ⇔
) ⇔  ,
,  .
. .
. :=
:= 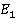 ,..., хп:= Еп]
,..., хп:= Еп] виразів
виразів  ,і = 1,2 ,...,п. Наприклад, якщо Р- програма з попереднього прикладу, то
,і = 1,2 ,...,п. Наприклад, якщо Р- програма з попереднього прикладу, то .
. ,
, 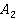 ,..., Ап, В - деякі константні вирази такі, що simp(
,..., Ап, В - деякі константні вирази такі, що simp(  ) =
) =  simp(B) = b, і = 1,2,...,n. Тоді
simp(B) = b, і = 1,2,...,n. Тоді 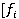 ]р(
]р( ,
,  , … ,ап)
, … ,ап) 
 )
) 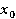 ,
,  ,
,  )? - запит.
)? - запит.


