
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функції на просторі послідовностейСодержание книги
Поиск на нашем сайте
Алфавіт X - довільна не порожня множина. Ланцюжки часто називають також словами, фразами і реченнями. Порожній ланцюжок позначається спеціальним символом Довжиною |ω| ланцюжка
Визначення 9.9. Функція
Для обчислення значення
Рис. 9.4. Схема обчислення індуктивної функції
Схема обчислення індуктивного функції нагадує метод доказу за індукцією. Аналогом бази індукції є обчислення Схема обчислення індуктивної функції дозволяє легко побудувати програму типу "S0; while (e) S;", яка одержує на кожній наступній ітерації циклу черговий елемент Простим і корисним прикладом, ілюструє схему обчислення індуктивної функції, є задача знаходження значення багаточлена, заданого послідовністю його коефіцієнтів.
Зауважимо, що
Текст програми. Методи доказу правильності програм, побудованих за допомогою схеми обчислення індуктивних функцій, і узагальнення цієї схеми, що дозволяє застосовувати аналогічний підхід для функцій, які не є індуктивними, будуть розглянуті нижче.
Завдання для самостійного вирішення
За використання схеми обчислення інваріантної функції необхідно вказати множини X, Yі
ВКАЗІВКА. Нехай
Скориставшись ними і формулами
легко визначити рекурсивну функцію не від’ємного цілого аргументу
Тут операція
ЗАВДАННЯ 9.32. Напишіть програму, що знаходить найбільший спільний дільник
ВКАЗІВКИ. Скористайтеся інваріантністю функції
Не забудьте довести Т інваріантність функції F
Лекція 10.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

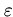 , а множину всіх ланцюжків над алфавітом X прийнято позначати Х*.
, а множину всіх ланцюжків над алфавітом X прийнято позначати Х*. називається кількість вхідних у неї символів. Множину усіх ланцюжків довжини не менш k позначають через
називається кількість вхідних у неї символів. Множину усіх ланцюжків довжини не менш k позначають через 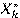 . Справедлива наступна послідовність включень:
. Справедлива наступна послідовність включень:
 конкатенації (або зчеплення) двох ланцюжків визначена наступним чином. Нехай
конкатенації (або зчеплення) двох ланцюжків визначена наступним чином. Нехай  ,
,  , тоді
, тоді  .
. називається індуктивною, якщо
називається індуктивною, якщо  можна обчислити, знаючи
можна обчислити, знаючи  і x, тобто якщо
і x, тобто якщо 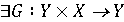 таке, що
таке, що  .
. . Вона індуктивна, так як для неї існує функція
. Вона індуктивна, так як для неї існує функція  , визначена формулою
, визначена формулою  , яка задовольняє попереднім визначенням.
, яка задовольняє попереднім визначенням. застосовується наступна cхема.
застосовується наступна cхема. ,
, 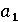 ,
,  ,
,  Спочатку обчислюється значення
Спочатку обчислюється значення 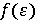 функції f на порожній ланцюжку
функції f на порожній ланцюжку 
 на подовженому ланцюжку
на подовженому ланцюжку  з використанням обчисленого на попередньому кроці значення
з використанням обчисленого на попередньому кроці значення  ланцюжка (послідовності)
ланцюжка (послідовності)  , яка знаходить значення
, яка знаходить значення  , умовою продовження
, умовою продовження 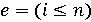 , S0 має обчислювати
, S0 має обчислювати  , де
, де 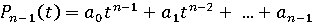 . Тому функція
. Тому функція  , визначена, як
, визначена, як  , задовольняє співвідношенню
, задовольняє співвідношенню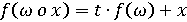 , що доводить її індуктивність. Відображення
, що доводить її індуктивність. Відображення  діє за формулою
діє за формулою  , а
, а  , що призводить до наступної програми.
, що призводить до наступної програми. , функцію F і перетворення T (див. визначення інваріантної функції) та пояснити програмну реалізацію перетворення T.
, функцію F і перетворення T (див. визначення інваріантної функції) та пояснити програмну реалізацію перетворення T. у заданій точці
у заданій точці  . Коефіцієнти багаточлена зберігаються в масиві а в порядку убування ступенів і є цілими числами, так само як і значення
. Коефіцієнти багаточлена зберігаються в масиві а в порядку убування ступенів і є цілими числами, так само як і значення  змінювати в програмі не можна.
змінювати в програмі не можна. . Продиференціюємо по x рівність
. Продиференціюємо по x рівність  та підставимо потім
та підставимо потім  . Ми отримаємо наступні співвідношення:
. Ми отримаємо наступні співвідношення:

 ,
, ,
, 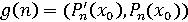 для обчислення якої і пишеться програма.
для обчислення якої і пишеться програма. .
.  При написанні програми величини
При написанні програми величини 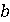 змінювати не дозволяється, слід використовувати інваріант
змінювати не дозволяється, слід використовувати інваріант  і обмежуючу функцію h = у.
і обмежуючу функцію h = у. двох цілих невід'ємних чисел
двох цілих невід'ємних чисел  та
та  не рівних одночасно нулю. Скористайтеся наступною властивістю найбільшого загального дільника (доведіть її!):
не рівних одночасно нулю. Скористайтеся наступною властивістю найбільшого загального дільника (доведіть її!):
 дозволяє знайти залишок від ділення
дозволяє знайти залишок від ділення 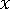 на
на  .
. ,
, 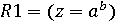 . При написанні програми величини
. При написанні програми величини  ,
,  інваріантної щодо перетворення
інваріантної щодо перетворення  , що задається формулою
, що задається формулою 
 двох цілих невід'ємних чисел
двох цілих невід'ємних чисел 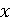 і
і  і не використовувати операцій ділення і знаходження залишку від ділення (допустимо поділ навпіл, реалізоване з допомогою операції зсуву). Скористайтеся наступними властивостями найбільшого загального дільника (доведіть їх!):
і не використовувати операцій ділення і знаходження залишку від ділення (допустимо поділ навпіл, реалізоване з допомогою операції зсуву). Скористайтеся наступними властивостями найбільшого загального дільника (доведіть їх!):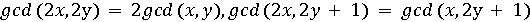 .
. щодо наступного перетворення T:
щодо наступного перетворення T:



