
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальні граматики. НБФ-граматикаСодержание книги
Поиск на нашем сайте
Граматикою називається формальний опис синтаксису мови програмування. Граматика визначається набором правил (іноді їх називають правилами підстановки), які визначають побудову із лексем достовірних програм. Формальна граматика використовує строгу систему позначень. Існують різні типи граматик. НБФ-граматика (граматика Наура-Бэкуса або граматика Бэкуса-Наура - БНФ-граматика) є контекстно-вільною граматикою. Ця граматика використовує НБФ-нотації, запропоновані Джоном Бэкусом в кінці 50-х років для опису синтаксису мови ALGOL. Проста НБФ-нотація дозволяє описувати всі достовірні конструкції мови програмування, використовуючи наступні символи:
Значення, які стоять поза дужками < >, називаються термінальними символами. НБФ-граматика складається із набору правил (їх іще називають мета лінгвістичними формулами або продукціями), які записуються за допомогою НБФ-нотації. Наприклад: <цифра>::= 0|1|2|3|4|5|6|7|8|9<цілочисельне значення>::= цифра | цифра <цілочисельне значення>Тут символи 0, 1, 2, 3 и т.д. будуть термінальними символами. При побудові граматики, що описує мову програмування, виділяють початковий не термінальний символ, який визначає конструкцію "програми". Існують граматики породження і граматики розпізнання. Породжуюча граматика генерує множину ланцюжків термінальних символів із початкового символу, а розпізнаюча граматика використовується для побудови по ланцюжку символів дерева граматичного розбору, яке і приведе до початкового символу. Можна сказати, що граматика складається із множин термінальних і не термінальних символів, початкового не термінального символу і набору правил. В 1959 році Ноам Хомський запропонував таку класифікацію граматик:
Розширена НБФ-нотація вводить ряд додаткових елементів, які дозволяють значно покращити наглядність представлення правил НБФ-граматики:
Рядки і мови Визначимо мову, як множину. Таке визначення мови може здатися незвичайним, однак воно корисне, тому що для мов, визначених як множини, виконується ряд відношень та операцій і цей фактор має вирішальне значення. Слова (послідовності букв) утворюють мову, як наприклад, перелік слів утворює спеціальний словник. Речення природної мови (послідовності слів, знаки пунктуації, і т. д.) практично неможливо перерахувати, але їх можна розглядати як множини. Звичайний розмовник містить множину, наприклад, англійських речень та їх іншомовних еквівалентів, придатних для бесіди. Такі розмовники, слідуючи нашому визначенню, також являються мовами. Однак в програмуванні мови з підходящою внутрішньою структурою елементів можна визначити на власний розсуд. Цілком природно використовувати підхід з позиції теорії множини для описання таких мов. Фактично формальна мова визначається як множина, елементи якої в свою чергу визначені виключно з допомогою операцій та відношень на множинах без використання природної мови або результатів досліду. Розглянемо, наприклад, наступні два визначення множин: D= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
де I – мова, яка дозволяє описати всі цілі десяткові числа. Ця мова включає два визначення, що охоплюють граматику мови. В подальшому будуть корисні наступні додаткові терміни: 1. Кожне із визначень називається продукцією. 2. Визначені назви множин (наприклад D та I) це фрази (або не термінальні символи). 3. Символи мови (0,1, 2, …, 9) носять назву термінальних символів. Сукупність всіх термінальних символів утворює алфавіт. 4. Особлива фраза (в нашому прикладі I), яка визначає множину, що включає всі елементи мови, називається типовою фразою. Якщо граматика розширюється двома новими продукціями ED={0, 2, 4, 6, 8}
та EI визначається як типова фраза мови, то змінена мова складається із парних десяткових чисел. Далі, якщо добавлена наступна продукція: OI=I-EI та EI визначається як типова фраза, то мова складається з непарних цілих чисел. І нарешті, якщо добавляються P={.}
і DN визначена як типова фраза, то мова включає всі десяткові числа. Замітимо, що в кінцевій граматиці продукції, що визначають I, ED, EI та OI, зайві. Оскільки мови – це множини, дуже корисно для формування мов ввести нову операцію над множинами, що називається мовним добутком та визначену як
Це означає, що мовний добуток двох множин рядків є множина, сформована зчепленням кожного елемента першої множини з кожним елементом другої множини. Визначимо різницю між операціями A
то
і
Таким чином елементи множин А і В зберігають свою тотожність в
Щоб проілюструвати використання мовного добутку, введемо нове означення десяткових цілих чисел I, використовуючи рекурсію
замість нескінченного об'єднання, використаного раніше. Цей запис можна прочитати наступним чином: "ціле (І) являється десятковою цифрою (D) або цілим числом, за яким іде десяткова цифра". Протилежно цьому зауважимо, що рекурсія
є не визначенням цілих чисел, а об'єднанням спискових структур у вигляді
Для подальшого пояснення мови буквено-цифрових послідовностей, першим символом в яких є буква (множина ідентифікаторів програм), задамо наступною граматикою, де перша продукція визначає типову фразу:
A={a, b, …, z} D={0, 1, …, 9}
Нерекурсивна (безкінечне об'єднання) форма ID має вигляд
Ця форма запису є більш громізткою. Форма Бекуса - Науро (БНФ) Формальні граматики часто визначаються за допомогою спеціальної системи позначень, яка називається формою Бекуса - Науро (БНФ), якій притаманні наступні особливості: 1. Результатом операції мовного добутку є розташування фраз поруч одна з другою. 2. Поруч знаходяться фрази, які повинні відокремлюватися кутовими дужками <>; наприклад, <А>, <арр1е>, <х≥3>. 3. Елементи алфавіту мови (тобто множина термінальних символів) є літерами. 4. Символ визначення фрази, використовуваний в продукції, позначається:: =, але не знайомий =, наприклад, <2-розрядні цілі>::= <цифра> <цифра> 5. Символ об'єднання U замінюється вертикальною рисою |. 6. Якщо фраза, визначена за допомогою формальної граматики, складається з двох частин, то результуюча фраза виходить об'єднанням складових (але не перетинанням, як прийнято в математиці). наприклад, <ціле>::= <цифра> <ціле>::= <цифра> <цифра> відповідає <ціле>::= <цифра> | <цифра> <цифра> 7. Повторювані мовні операції вводяться за допомогою префіксів * +, які позначають відповідно об'єднання нуля або більше, одного або більше повторень фраз відповідно. Наприклад, десяткове ціле можна визначити як <ціле>::= + (<цифра>) а визначення послідовності, що має нуль або більше точок, має вигляд *(.) Верхній індекс, використовуваний разом з символами *, + означає максимальне число повторень. Так, вираз <имя>:: = визначає ім'я, що включає від однієї до п'яти букв, за якими може слідувати одна цифра. (Зазвичай символ * використовується в якості індексу оператора повторення, але тут ми відійдемо від традиції і будемо вживати його в якості префікса.) Формальна граматика, в якій кожне визначення має форму <ім’я>::= (будь-який мовний вираз) називається контекстно-вільною граматикою (КВГ). Як було показано вище на прикладі цілих чисел, КВГ може бути рекурсивною. Множина продукції (визначень) КВГ разом з типовою фразою визначають мову, причому визначення типової фрази саме є граматикою. Наприклад, граматика для формування повідомлення про час доби {00:00,..., 23:59} може бути задана у формі, в якій <час> слугує типовою фразою: <час>::=<години> <хвилини> <години>::=0<цифра>│1 <цифра>│2 <цифра до 3> <хвилини>::=<цифра не більше 5> <цифра> <цифра до 3>::=0│1│2│3 <цифра до 5>::=<цифра не більше 3>│4│5 <цифра>::=<цифра не більше 5> 6│7│8│9 Якщо кожне визначення задано в формі <ім’я>::=x<ім’я 1>, де x є будь-якою символьною послідовністю, а <ім’я 1> може бути ім’ям порожнього рядка, тоді така граматика називається регулярною. Прості визначення мови дозволяють отримати синтаксичну діаграму, що має вигляд графа зі шляхами, відповідними продукціями. Наприклад, граматика мови програмування може
Рис.5.2. бути представлена так, як показано на рис. 5.2.. Вибір між формальними граматиками і синтаксичними діаграмами залежить від конкретної ситуації. Діаграми більш наочні, але граматики дозволяють більш легко формалізувати процеси і являються гнучким засобом формування і запису мовних структур. Регулярні вирази Регулярним виразом називається права частина продукції, яка визначає мову з допомогою операції зчеплення (мовного добутку), об'єднання і повторення. (Визначення мови на <ім'я>::=((A|…|Z)*((A|…|Z) | (0|…|9)) Регулярний вираз дозволяє зробити опис мови доволі компактним. Система позначень регулярних виразів допускає декілька можливостей для представлення ідентичних мов, що у випадку необхідності дозволяє спростити, наприклад так, як показано нижче +(А)*(А)=*(А)+(А)=+(А) *(А)*(А)=*(А) А*(А)=*(А)А=+(А) А *(*(А))=*(А) А(В|C)=(AB) | (AC), (B|C)A=(BA) | (CA) А(В|C)=(AB) C + (A) | Є цікаве застосування регулярних виразів для оптимізації структур управління. В цьому випадку оператори програми розглядаються як рядки, які можуть бути сформовані за допомогою всіх можливих обчислювальних форм мови.
Отримані структури можна спростити, щоб отримати більш просту програму. Наприклад, деякій програмі, відповідає регулярний вираз (без урахування предикатів): ((ВА)|(CA)) ((A*(A)) | Цей вираз може бути спрощений наступним чином: ((BA) | (CA)) (+(A) | = ((BA) | (CA)) * (A) = ((B | C)A) * (A) = (B | C) (A * (A)) =(B | C) + (A)
Лекція 6. Java - мова ООП
Вибір цієї мови в якості базового для нашого курсу обумовлений перш за все наявністю у нього таких якостей, як простота і міць, безпека, об'єктна орієнтованість, надійність, інтерактивність, архітектурна незалежність, можливість інтерпретації, висока продуктивність і легкість у вивченні. Частина з них нам знадобиться з перших же кроків, інші - трохи пізніше.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.008 с.) |


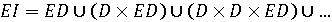
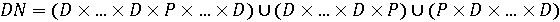
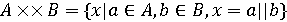
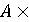 Bта
Bта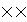 B. Зокрема якщо
B. Зокрема якщо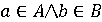
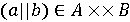 але
але 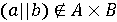
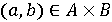 але
але 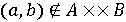
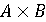 , але втрачають її в мовному добутку
, але втрачають її в мовному добутку 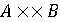 . Також зауважимо, що мовний добуток
. Також зауважимо, що мовний добуток 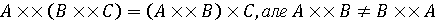
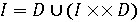
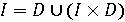
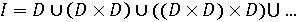
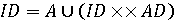
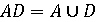
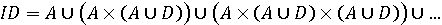
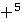 (<буква>)
(<буква>) 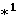 (<цифра>)
(<цифра>)



 <ім’я>::=
<ім’я>::=

 <буква>:: …
<буква>:: …



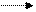 <цифра>::= …
<цифра>::= …

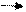
 =
= 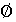 А=А
А=А


