Знаходження інваріанта циклу і доведення правильності
У попередній лекції ми вже познайомилися з технікою проектування циклу за допомогою інваріанту, що дозволяє значно спростити написання програм. Питання знаходження інваріантів циклів і докази правильності програм - основна тематика цієї лекції.
Умови правильності циклу
Теоремою, на якій базується схема проектування циклу за допомогою інваріанта, є наступне твердження, яке ми приймемо без доведення. Його істинність може бути виведена з властивостей перетворювача предикатів  та визначення оператора циклу. та визначення оператора циклу.
Теорема 10.1. Якщо
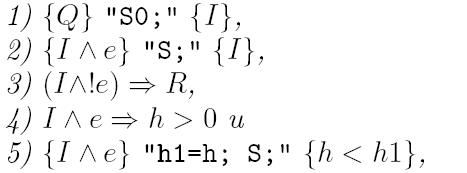
тоді специфікація програми {Q} "S0; while (e) S;" {R} є тавтологією.
Доведемо за допомогою цієї теореми правильність деяких програм, побудованих в попередньому параграфі.
Текст програми.
public class MulI {
public static void main (String [] args) throws Exception {
int a = Xterm.inputInt ("a ->");
int b = Xterm.inputInt ("b ->");
int x = a, y = b, z = 0;
while (y> 0) {
if ((y & 1) == 0) {
y>>> = 1; x + = x;
} Else {
y -= 1; z + = x;
}
}
Xterm.println ("a * b =" + z);
}
}
Перевіримо складові Теореми 1.1:
1)  , ,
 . .
2) Для того щоб перевірити, що предикат  є тавтологією, обчислимо заздалегідь є тавтологією, обчислимо заздалегідь  . .
 ("If ((y & 1) = 0) {y / = 2; x + = x;} else {y-= 1; ("If ((y & 1) = 0) {y / = 2; x + = x;} else {y-= 1;
z + = x;}",  парний парний  "y / = 2; x + = x;" "y / = 2; x + = x;"  непарний непарний  ("y- = 1; z + = x; ", ("y- = 1; z + = x; ",  непарний непарний  парний парний  непарний непарний  парний) ⋁ ( парний) ⋁ ( непарний непарний  парний парний  непарний непарний  парнній парнній 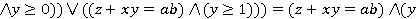 непарний непарний 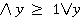 парний парний  . .
Далі маємо 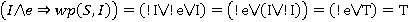 . .
3). 
Цей предикат представляє собою диз'юнкцію чотирьох членів і, очевидно, істинний, якщо пістинні перший або другий з цих членів. В іншому випадку  , і предикат приймає вигляд , і предикат приймає вигляд  . Таким чином . Таким чином  , - тавтологія. , - тавтологія.
4). 
5). Для перевірки останньої умови знайдемо wp("h1 = h; S;", h < h1) = wp ("h1 = y;" wp("if ((y & 1) == 0) {y / = 2; x + = x;} else {y-= 1; z + = x;} ", y < h1)) = wp(" h1 = y;,(y парний ⇒ wp("y / = 2; x + = x; ",y < h1)) ⋀ (y непарний ⇒wp(" y-= 1;
z + = x; ", y < h1))) = wp (" h1 = y; ",(y непарний ⋁y< 2 * h1) ⋀ (y парний ⋁ y < 2 * y) ⋀ (y непарний ⋁ y < 2 * y) ⋀ (y парний ⋁y<y+1) = (y непарний ⋁ y < 2 * y) ⋀ (y парний ⋁T) = (y непарний  непарний ⋁y<2*y) = (y непарний. ⋁y > 0). непарний ⋁y<2*y) = (y непарний. ⋁y > 0).
Тоді маємо (I ⋀ e ⇒ wp("h1 = h; S;", h<h1)) = (y < 0 ⋁ z + xy ≠ab ⋁ y ≤ 0 ⋁ y непарний, непарний)⋁(y≤0⋁y>0)) = ((y<0⋁z+xy≠ab⋁y непарний) ⋁ T) = T, що завершує доказ правильності написаної програми.
Доведемо часткову правильність ще однієї побудованої в попередньому параграфі програми.
Текст програми.
public class Gcd {
public static void main (String [] args) throws Exception {
int x = Xterm.inputInt ("x ->");
int y = Xterm.inputInt ("y ->");
Xterm.print ("gcd (" + x + "," + y + ") =");
while ((x! = 0) & & (y! = 0)) {
if (x> = y) x -= y;
else y -= x;
}
Xterm.println ("" + (x + y));
}
}
Якщо в якості обмежуючої функції взяти  , тоді правильність отриманої програми легко може бути доведена. Позначимо через , тоді правильність отриманої програми легко може бути доведена. Позначимо через  і і  початкові значення змінних x і y, які відповідають передумові початкові значення змінних x і y, які відповідають передумові  . .
Зауважимо також, що постумова програми в цілому може бути записана у вигляді предиката R1 = (надрукований 𝑔cd (x,y), а постумовою циклу є предикат  . .
1)  ";", ";",  . .
2) Збереження інваріанта після виконання тіла циклу випливає з T – інваріантності  . Формальну перевірку проведіть самостійно. . Формальну перевірку проведіть самостійно.
3)  . .
4) Формальне доказ проведіть самостійно.
5) Формальне доказ проведіть самостійно.
6) Для завершення доказу правильності програми необхідно ще показати, що є тавтологією  . Так як формального визначення операторів друку ми не розглядали, будемо вважати, що предикат . Так як формального визначення операторів друку ми не розглядали, будемо вважати, що предикат  , а S1 має вигляд "z = x + y;". , а S1 має вигляд "z = x + y;".
 . .
Отримана диз'юнкція істинна, якщо помилкова умова  . В іншому випадку один з аргументів функції . В іншому випадку один з аргументів функції  дорівнює нулю і за відповідної властивості найменшого спільного дільника істинним є другий диз'юнктивний член, що завершує доказ правильності програми. дорівнює нулю і за відповідної властивості найменшого спільного дільника істинним є другий диз'юнктивний член, що завершує доказ правильності програми.
Теорія повітряної кульки
До цих пір ми використовували для побудови програм готові, не відомо звідки взяті інваріанти. На практиці, звичайно, постановка задачі не включає в себе інваріант. Однак будь-яка коректна постановка задачі містить її передумову-і післяумову:  "S0; while (e) S;" {R}, тому вони і повинні послужити (слугувати) основою для побудови інваріанту. "S0; while (e) S;" {R}, тому вони і повинні послужити (слугувати) основою для побудови інваріанту.
Тепер потрібно зрозуміти, який саме з двох предикатів Q й R є більш важливим для побудови інваріанту. Наведемо два аргументи на користь післяумови R.
Перший такий: передумова Q досить часто має вигляд T, що відповідає відсутності обмежень на початкові умови, в яких повинна правильно працювати програма. Зрозуміло, що в цьому випадку інваріант можна будувати тільки виходячи з післяумови R.
Другий аргумент: уявімо собі R у вигляді мети, якої повинен досягти подорожній на місцевості, а Q у вигляді точки його початкового розташування. Інваріант, який ми хочемо побудувати, повинен допомогти подорожньому досягти потрібної йому мети. Чи можна сподіватися на це, повністю проігнорувавши R?
Якщо не пам'ятати постійно про мету в процесі написання програми, то дуже малоймовірно, що вона все ж виявиться досягнутою. З якої б початкової точки мандрівник не вийшов, якщо у нього немає мети, він до неї не добереться!
Саме з цієї причини програмування називають цілеспрямованою діяльністю, а за основу для побудови інваріанта беруть післяумову R.
Розглянемо геометричну ілюстрацію завдання що стоїть перед нами, зобразивши на множині X всіх значень програмних змінних підмножини   , друга з яких задається післяумовою R, а перша представляє множину, яка може бути отримана з , друга з яких задається післяумовою R, а перша представляє множину, яка може бути отримана з  після виконання сукупності простих присвоювань S0. Шуканому інваріанту циклу I на рисунку 10.1 повинна відповідати якась поки невідома нам множина після виконання сукупності простих присвоювань S0. Шуканому інваріанту циклу I на рисунку 10.1 повинна відповідати якась поки невідома нам множина  . .
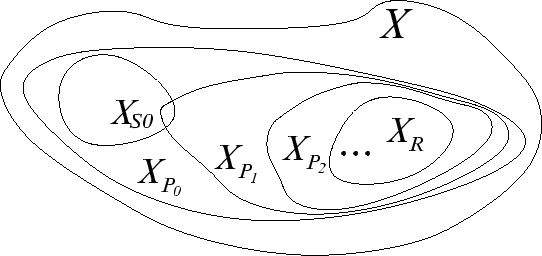
Рис. 10.1. Теорія повітряної кульки
Існує дуже красивий опис того, що відбувається з множиною змінних програми в процесі виконання циклу, званий теорією повітряної кульки.
Розглянемо послідовність предикатів  , , 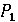 ,…, ,…,  , які описують множину змінних до початку циклу, після його першої ітерації, …, після n -ої (останньої) ітерації. , які описують множину змінних до початку циклу, після його першої ітерації, …, після n -ої (останньої) ітерації.
Множини, що визначаються цими предикатами, представляють послідовність вкладених одна в одну множин, причому 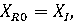 а а  . Зручно уявляти собі ці множини як послідовні стани спочатку надутої повітряної кульки, з якої на кожній черговій ітерації циклу випускають трохи повітря. . Зручно уявляти собі ці множини як послідовні стани спочатку надутої повітряної кульки, з якої на кожній черговій ітерації циклу випускають трохи повітря.
Використовуючи цю модель, можна сказати, що побудова інваріанта вимагає так надути кульку, що знаходиться в стані  , щоб він став містити множину , щоб він став містити множину  . З математичної точки зору необхідно послабити предикат . З математичної точки зору необхідно послабити предикат  до такої міри, щоб істинність цього ослабленого предиката (який і буде взятий за інваріанта до такої міри, щоб істинність цього ослабленого предиката (який і буде взятий за інваріанта 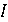 ) могла бути отримана з істинного ) могла бути отримана з істинного 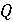 за допомогою простих початкових присвоювань за допомогою простих початкових присвоювань  . .
Отже, основним методом побудови інваріанта є ослаблення післяумови оператора циклу. При цьому часто вдається отримати і умову продовження циклу (що по-суті еквівалентно визначенням обмежуючої функції), взявши в якості її заперечення того предиката, яким ми послабили післяумову.
Реально застосовуються три перші з наступних нижче наведених методів побудови інваріанту.
1) Усунення кон'юнктивного члена. Предикат 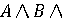 C можна ослабити до C можна ослабити до  . .
2) Заміна константи змінної. Предикат  може бути ослаблений до може бути ослаблений до  , де , де  - нова змінна. - нова змінна.
3) Розширення області значень змінної. Предикат 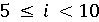 можна ослабити до можна ослабити до  . .
4) Додавання диз'юнктивного члена. Предикат A можна послабити до A ⋁ B, де B - деякий інший предикат.
Причина того, що четвертий метод не застосовується, дуже проста - він не містить ніяких рекомендацій з приводу того, як саме вибрати предикат. Решта методів побудови інваріанта циклу будуть проілюстровані у наступних секціях цього пункту в процесі вирішення різних завдань.
|



 та визначення оператора циклу.
та визначення оператора циклу.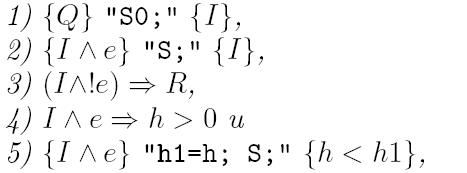
 ,
, .
. є тавтологією, обчислимо заздалегідь
є тавтологією, обчислимо заздалегідь  .
. ("If ((y & 1) = 0) {y / = 2; x + = x;} else {y-= 1;
("If ((y & 1) = 0) {y / = 2; x + = x;} else {y-= 1; парний
парний  "y / = 2; x + = x;"
"y / = 2; x + = x;"  непарний
непарний  непарний
непарний  парний
парний  непарний
непарний  парний) ⋁ (
парний) ⋁ ( непарний
непарний  парний
парний  непарний
непарний  парнній
парнній 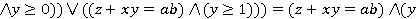 непарний
непарний 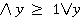 парний
парний  .
.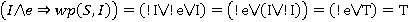 .
.
 , і предикат приймає вигляд
, і предикат приймає вигляд  . Таким чином
. Таким чином  , - тавтологія.
, - тавтологія.
 непарний ⋁y<2*y) = (y непарний. ⋁y > 0).
непарний ⋁y<2*y) = (y непарний. ⋁y > 0). , тоді правильність отриманої програми легко може бути доведена. Позначимо через
, тоді правильність отриманої програми легко може бути доведена. Позначимо через  і
і  початкові значення змінних x і y, які відповідають передумові
початкові значення змінних x і y, які відповідають передумові  .
. .
. ";",
";",  .
. . Формальну перевірку проведіть самостійно.
. Формальну перевірку проведіть самостійно. .
. . Так як формального визначення операторів друку ми не розглядали, будемо вважати, що предикат
. Так як формального визначення операторів друку ми не розглядали, будемо вважати, що предикат  , а S1 має вигляд "z = x + y;".
, а S1 має вигляд "z = x + y;". .
. . В іншому випадку один з аргументів функції
. В іншому випадку один з аргументів функції  дорівнює нулю і за відповідної властивості найменшого спільного дільника істинним є другий диз'юнктивний член, що завершує доказ правильності програми.
дорівнює нулю і за відповідної властивості найменшого спільного дільника істинним є другий диз'юнктивний член, що завершує доказ правильності програми. "S0; while (e) S;" {R}, тому вони і повинні послужити (слугувати) основою для побудови інваріанту.
"S0; while (e) S;" {R}, тому вони і повинні послужити (слугувати) основою для побудови інваріанту.
 , друга з яких задається післяумовою R, а перша представляє множину, яка може бути отримана з
, друга з яких задається післяумовою R, а перша представляє множину, яка може бути отримана з  після виконання сукупності простих присвоювань S0. Шуканому інваріанту циклу I на рисунку 10.1 повинна відповідати якась поки невідома нам множина
після виконання сукупності простих присвоювань S0. Шуканому інваріанту циклу I на рисунку 10.1 повинна відповідати якась поки невідома нам множина  .
.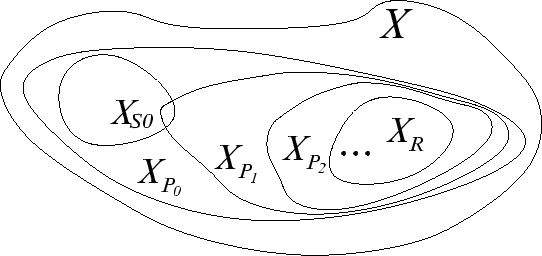
 ,
, 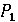 ,…,
,…,  , які описують множину змінних до початку циклу, після його першої ітерації, …, після n -ої (останньої) ітерації.
, які описують множину змінних до початку циклу, після його першої ітерації, …, після n -ої (останньої) ітерації.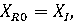 а
а  . Зручно уявляти собі ці множини як послідовні стани спочатку надутої повітряної кульки, з якої на кожній черговій ітерації циклу випускають трохи повітря.
. Зручно уявляти собі ці множини як послідовні стани спочатку надутої повітряної кульки, з якої на кожній черговій ітерації циклу випускають трохи повітря. до такої міри, щоб істинність цього ослабленого предиката (який і буде взятий за інваріанта
до такої міри, щоб істинність цього ослабленого предиката (який і буде взятий за інваріанта 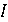 ) могла бути отримана з істинного
) могла бути отримана з істинного 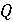 за допомогою простих початкових присвоювань
за допомогою простих початкових присвоювань  .
.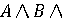 C можна ослабити до
C можна ослабити до  .
. може бути ослаблений до
може бути ослаблений до  , де
, де  - нова змінна.
- нова змінна.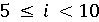 можна ослабити до
можна ослабити до  .
.


