
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад і властивості алгоритмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задача 2.1. Нехай нам потрібно вирішити задачу знаходження найменшого простого дільника натурального числа
Алгоритм 2.1: П1: Покласти ціле число П2: Якщо П3: Збільшити значення Для того щоб зрозуміти цей алгоритм, треба виступити в ролі комп'ютера (або скоріше навіть універсального виконавця команд), виконуючи вручну зазначену в ньому послідовність дій для деяких невеликих значень
Основні властивості будь-якого алгоритму - це завершеність, визначеність, вхід (введення), вихід (висновок) і ефективність. Розглянемо їх послідовно більш докладно.
Вхід (вхід). Алгоритм завжди має деяку (іноді рівну нулю) кількість вхідних даних, тобто величин, переданих йому до початку роботи. В алгоритмі 7.1,, наприклад, вхідна величина одна - ціле число
Кажуть, що на ЕОМ практично неможливо працювати з дійсними числами. Більш того, навіть із справжніми цілими числами на комп'ютері працюють не так вже й часто. Зазвичай замість множин цілих
про те, що ми маємо справу не з справжніми числами, але іноді особливості подання чисел в ЕОМ виявляються досить несподіваним чином.
Відомо, що всі визначення алгоритму еквівалентні щодо можливості моделювання обчислень. Форма задання алгоритму особливої ролі не відіграє, важливим є тільки вибір мінімальних засобів для задання і перетворення інформації. Прикладна теорія алгоритмів спрямована на дослідження моделей алгоритмів. Тут під алгоритмом розуміють довільне перетворення обчислювальної інформації, яке може бути виражене за допомогою деякої алгоритмічної мови. Алгоритмічна мова буває різного типу складності. У зв’язку з обчислюванням алгоритмів на комп’ютерах виберемо як форму запису алгоритму мову Паскаль. Розглянемо такий приклад. Нехай потрібно дослідити розв’язання повного квадратного рівняння Алгоритм дослідження можна описати українською мовою за допомогою такої послідовності кроків:
0. Ввести значення a, b, c. 1. Обчислити дискримінант 2. Якщо В іншому разі, якщо Інакше (якщо 3. Кінець алгоритму.
Якщо уважно подивитися на таке задання алгоритму, то можна виділити основні недоліки опису: громіздкість та неоднозначність трактувань інструкцій. Для їх усунення використовують спеціалізовані формалізми: блок-схеми, мови програмування тощо. Наш алгоритм можна описати блок-схемою, яку зображено на рис. 2.1. Блок-схема є зв’язним орієнтованим графом, вузли якого можуть бути блоками чотирьох типів: блок ініціалізації (ввести значення a, b, c), функціональні блоки (обчислити Для дослідження цієї задачі на ЕОМ слід описати алгоритм дослідження за допомогою якоїсь мови програмування. Таке задання називають програмою.
Структура програми більшості мов програмування типова і має загальний характер. Розглянемо запис програми 1.1 дослідження розв’язання повного квадратного рівняння в мові програмування Паскаль. program EХ1_1; var A, B, C, D: real; Begin read (A, B, C); D:= B*B – 4*A*C; if D = 0 then writeln (‘Рівняння має один розв’язок x = ‘, –B/(2*A)) Else if D > 0 then writeln (‘Рівняння має два корені x 1 = ‘, (–B + D)/(2*A), ‘ i x 2 = ‘, (–B – D)/(2*A)) Else writeln (‘Рівняння не має дійсних коренів’); end. Програма 1.1. Дослідження розв’язку повного квадратного рівняння
Знання англійської мови дає змогу зрозуміти в загальних рисах призначення кожної інструкції (відділяється крапкою з комою) у програмі. Програми Паскаль, як і програми більшості мов програмування, складаються з таких основних частин: заголовка (program), блока опису констант (const), блока конструювання типів (type), блока опису змінних (var), блока опису процедур та функцій і блока виконань (begin–end). Заголовок програми, в нашому прикладі іменується EХ1_1, використовується для ідентифікації програми і може містити опис пристроїв введення-виведення інформації. Блок опису змінних використовують для визначення розмірів ділянок пам’яті, де процесор оброблятиме інформацію для отримання кінцевого результату. У цьому випадку змінні A, B, C, D виступають у ролі засобів доступу до ділянок пам’яті (імен), а опис real визначає розмір пам’яті, що виділяється для змінної зазначеного типу у разі отримання даної програми на виконання процесором. Блок опису констант використовують для визначення даних, що не змінюють своїх значень за час виконання програми. За допомогою конструктора типів будують структури даних, зручні для побудови ефективних алгоритмів, яких немає серед стандартних типів даних вибраної мови програмування. Блок виконань містить інструкції, що описують послідовність дій, які процесор здійснюватиме над пам’яттю для отримання кінцевого результату алгоритму.
Спробуйте описати алгоритм дослідження квадратного рівняння Традиційно програми можна поділити на два класи: прикладні та системні. Прикладні програми використовують для розв’язання конкретних прикладних задач. Системні програми полегшують роботу користувача на комп’ютері. До системних програм належить і набір програм, який дістав назву операційна система (ОС). ОС забезпечує взаємодію між користувачем і комп’ютером, а також між програмою і різними компонентами апаратури комп’ютера. Загальне керування комп’ютером здійснюють за допомогою мови директив. У кожній ОС є набір службових програм (утиліт), які використовують для полегшення роботи у разі написання програм. Одна з типових конфігурацій ОС для комп’ютера має такі складові компоненти: файлову систему; драйвери зовнішніх пристроїв; процесор командної мови. Обчислювальні машини Обчислювальна машина - це автоматизована лічильна машина, створена для підвищення швидкості обробки арифметичних та інших математичних операцій. Обчислювальні машини є апаратною реалізацією скінченних автоматів. Вони можуть бути цифровими або аналоговими. Цифрова машина - це система, яка працює на числовій дискретній основі так, що число формально задається в середині системи. Будь-яка аналогова система має істотно неперервну основу, числа задаються фізичними величинами (промінь світла, струм тощо).
Для ілюстрації основної відмінності між цифровим і аналоговим принципом обробки інформації розглянемо класичний приклад з музичними інструментами. Баян можна назвати дискретною системою, тому що в ній довільну фіксовану ноту можна або грати, або ні, бо кожна нота (клавіша) дискретно відділена від наступної. Скрипка ж буде аналоговою системою, оскільки на скрипці висота тону може змінюватися безперервно. Відомо, що довільну аналогову машину теоретично можна апроксимувати деякою цифровою. Проте на практиці виникають труднощі реалізації. Наприклад, спроба імітації роботи людського мозку приводить до природних обмежень, пов’язаних з пам’яттю та часом. Цифрові обчислювальні машини (ЦОМ) можна поділити на певні класи відповідно до організації загальних принципів обчислень. Наприклад, можна виділити одноадресні, двоадресні, n-адресні обчислювальні машини. Ця відмінність ґрунтується на різниці в числі адрес у командних словах обчислювальної машини. Іншим прикладом поділу є два великі класи ЦОМ: послідовні та паралельні. Цей поділ використовує такий критерій: ЦОМ можуть виконувати одночасно одну або кілька операцій. Загальну схему ЦОМ ілюструє рис. 2.2. Слід зазначити, що не всі блоки, зображені на рисунку, присутні в усіх типах ЦОМ, але ця схема є найзагальнішою. Пам’ять обчислювальної машини зберігає список команд (програму) обробки даних і самі дані (набір чисел), які оброблятимуться цими операціями (командами). Керуючий пристрій визначає, які ж операції пересилатимуть числа в арифметичний пристрій для виконання необхідних операцій. Після виконання цих операцій дані повертаються в запам’ятовуючий пристрій.
Проведіть аналогії загальної схеми функціонування ЕОМ із загальною схемою функціонування деякого виробничого комплексу. Різні обчислювальні машини можуть використовувати різні коди для задання команд: десятковий, двійковий, вісімковий, шістнадцятковий тощо. Детально на цих кодах не зупинятимемося, тільки зазначимо, що довільне слово, число можна закодувати послідовністю двійкового коду 0 і 1. Для того щоб реалізувати певні дії, які слід застосовувати до даних, що знаходяться в пристрої запам’ятовування, ми повинні мати можливість вказувати процесору, які ж конкретні команди він має виконати над цими даними. Як ілюстрацію такого принципу розглянемо умовну триадресну обчислювальну машину, тобто машину, в якій командне слово містить три адреси: адреси двох чисел, що обробляються, і адресу, куди заносять результат обробки. Припустимо, ми вибрали таке кодування арифметичних операцій для триадресної машини: додавання (01), віднімання (02), множення (03), ділення (04), умовний перехід (05), завантаження (06), друк (07). Розглянемо таку просту арифметичну задачу. Нехай потрібно перемножити числа2 і 3, потім відняти 1 та надрукувати результат. Перше, що слід зробити,- розмістити числа 2, 3, 1 у вільних регістрах пам’яті. Нехай такими будуть регістри з номерами 500, 501, 502. Для позначення цієї дії використаємо запис 06/500(2), 06/501(3), 06/502(1). Для триадресної машини команди мають таку структуру: І / A 1/ A 2/ A 3, де І - код команди, А 1, А 2, А 3 - адреси регістрів. Тоді для реалізації нашої задачі потрібно написати програму: 03/500/501/500 02/500/502/503 07/503
Для кращого зберігання операндів і операцій в пам’яті обчислювальної машини Ньюел у 1961 р. запропонував використовувати списки. Базовим елементом списку є елемент, зображений на рис. 2.3.
Список можна використати для «зв’язування» різних елементів пам’яті, які «фізично» містяться в непослідовних фрагментах пам’яті ЦОМ. Так вираз
Мак-Каллок і Піттс довели, що будь-яку обчислювальну функцію можна реалізувати за допомогою спеціально організованої мережі ідеальних нейронів, логічні властивості яких з високою вірогідністю можна приписати реальному нейрону. Ця мережа матиме наступні вади. По-перше, проблема полягає в тому, чи можна знайти якийсь розумний принцип реорганізації мережі, який давав би змогу випадково об’єднаній спочатку групі ідеальних нейронів самоорганізовуватись в «обчислювальний пристрій», здатний розв’язувати довільну задачу. По-друге, потрібно використовувати велику кількість нейронів. Так, модель роботи мозку мурашки потребує використання близько 20 000 нейронів, що на практиці реалізувати неможливо. Нейрокомп’ютер – програмно-технічна система (спеціалізована ЕОМ), що реалізує деяку формальну модель природної мережі нейронів. Про важливість розвитку цього напряму свідчить і те, що в основу побудови обчислювальних пристроїв п’ятого покоління покладено ідею паралельної обробки інформації в нейроноподібних системах. Незважаючи на те, що один електричний процесор працює в тисячі разів швидше, ніж його нейронний еквівалент у мозку, мережі нейронів розв’язують багато задач (особливо нечислових) в тисячі разів швидше, ніж електронний процесор. Причина цього в наступному: 1) характер взаємозв’язків між нейронами дає змогу робити розв’язання багатьох задач, а також реалізацію різних функцій – у паралельний спосіб; 2) у нейронній мережі пам’ять не локалізована в одному місці (як в послідовних машинах), а розподілена по всій структурі; у біологічних системах пам’ять реалізується підсиленням або послабленням зв’язків між нейронами, а не зберіганням двійкових символів; 3) біологічні мережі реагують не на всі, а тільки на визначені зовнішні подразнення; кожен нейрон виступає як елемент прийняття рішення і елемент зберігання інформації; перевага такої структури – «життєздатність» (вихід з ладу декількох нейронів не спричинює значної зміни даних, що зберігаються, або руйнування всієї системи); 4) можливість адресації за вмістом є ще однією важливою характеристикою систем з розподіленою пам’яттю (кожен елемент відшукують за його вмістом, а не зберігають в комірці пам’яті з визначеним номером). В основу зв’язків у нейрокомп’ютерах покладено асоціативний принцип. Асоціативні зв’язки пронизують все мислення людини. Наприклад, результат операції Тому майбутнє – за комп’ютерами, які ґрунтуються на аналізі зв’язків, Моделі нейронних мереж і схеми з адресацією за змістом мають і недоліки. Внаслідок нефіксованої організації вони можуть плутати різні об’єкти. Це аналогічно звиканню, посиленню чуттєвості до асоціацій, які лежать в основі психологічних особливостей людини. Інакше кажучи, довільний комп’ютер, що претендує на «розумність», повинен мати такі особливості. Як було зазначено раніше, існує безліч мов програмування, які полегшують запис алгоритму розв’язання задачі. Для того щоб відповідні програми було виконано на конкретній машині, їх слід перевести в мову автокоду цієї машини. Для цього використовують інтерпретатори, асемблери і компілятори. Робота інтерпретатора ґрунтується на тому, що для задання кожної операції в машині використовують особистий символ, так що увесь набір операцій програми можна задати простими символами. Вони інтерпретуються і послідовно обробляються машиною. Асемблер застосовують до мов програмування, які дуже близькі до мови автокоду. Програму повністю перекладають з асемблерної мови в мову автокоду, а потім засилають на виконання. Компілятори відрізняються від асемблерів тільки тим, що одне слово може позначати набір операцій мови машинних команд. Слово комп’ютер походить від англійського слова to compute, яке означає «здійснювати обчислення». Інша назва комп’ютерів - електронні обчислювальні машини. Вона підкреслює два ключових аспекти. По-перше, комп’ютер - це сукупність апаратних засобів, призначених для обчислень і перетворення інформації. По-друге, основними елементами комп’ютерів є електронні прилади. Комп’ютер здійснює обчислення та інші інформаційні перетворення за допомогою програм, тобто певних послідовностей інструкцій. Можна вважати, що за допомогою програм здійснюється керування апаратними засобами комп’ютера. Найпростіші засоби для виконання простих арифметичних операцій були відомі людям у глибоку давнину. Перші механічні пристрої (арифмометри) створено в середині ХVII ст. Паскалем і Лейбніцом. У XIX ст. Чарльз Беббідж уперше сформулював ідею створення універсальної обчислювальної машини. Він розробив детальний проект, який не був закінчений через відсутність необхідної технічної бази. Значний внесок у розробку принципів функціонування комп’ютерів зробив Алан Тьюринг, який у 1937 р. описав гіпотетичну машину з універсальними можливостями. Ця машина Тьюринга, яку можна розглядати як одну з можливих формалізацій поняття «алгоритм», стала теоретичною основою сучасних комп’ютерів. Перша електронно-обчислювальна машина ENIAC створена у 1943–46 рр. Дж. У. Моклі та Дж. П. Екертом з Пенсільванського університету. Величезний внесок у розвиток обчислювальної техніки зроблено працею Дж. фон Неймана. Початок серійного виробництва ЕОМ пов’язують зі створенням у 1951 р. ЕОМ UNIVAC. Роботи над створенням першої вітчизняної ЕОМ МЕЛМ (малої електронної лічильної машини) були розпочаті в Інституті електротехніки АН УРСР у 1947–1948 рр. в м. Києві групою науковців під керівництвом С. О. Лебєдєва. У 1951 р. машину було прийнято до експлуатації. Як подальші віхи в розвитку обчислювальної техніки можна відзначити такі: поява операційних систем; виникнення мов програмування високого рівня; розвиток мережних технологій і масове розповсюдження персональних комп’ютерів. Комп’ютери можна класифікувати за різними критеріями. Основним з них є ступінь універсальності. Комп’ютери бувають спеціалізовані, призначені для виконання окремих задач, і універсальні. Універсальну машину можна визначити як машину, що в принципі може розв’язувати будь-яку задачу, для якої існує алгоритм виконання, або як машину, здатну реалізувати будь-який алгоритм. Надалі розглядатимемо лише цифрові універсальні машини, і якщо не буде явно вказано інше, під словом комп’ютер ми розумітимемо саме такі машини. Універсальний цифровий комп’ютер може реалізувати будь-який алгоритм. Інформація, яку обробляє комп’ютер, зберігається в його пам’яті у вигляді послідовності нулів та одиниць. Пам’ять складається з електронних схем, кожна з яких може перебувати в одному з двох стійких станів, один з них беруть за 0, а інший - за 1. Мінімальною одиницею інформації є біт. Біт - один двійковий розряд, за допомогою якого можна закодувати одне з двох можливих значень: 0 або 1. Зрозуміло, що для виконання обчислень цифровий комп’ютер повинен мати у своєму складі засоби, що дають змогу виконувати операції над двійковими розрядами, тобто реалізовувати булеві функції. Булевою називається функція, аргументи і результат якої можуть набувати одне Цифрові універсальні комп’ютери можна класифікувати за потужністю. Виділяють такі основні групи цих комп’ютерів. Суперкомп’ютери. Для них характерна наявність великої (десятки, сотні або тисячі) кількості процесорів, які сумісно розв’язують ту чи іншу задачу, тим чи іншим способом взаємодіючи між собою; у цьому разі забезпечується дуже висока сумарна потужність. Типове призначення - виконання надскладних розрахунків. Найпростіші суперкомп’ютери можна використовувати як корпоративні мережні сервери. У цьому разі їх називають майнфреймами. Як приклади суперкомп’ютерів можна навести IBM System/390, T/9000, RS/6000. Ще більшу потужність забезпечують суперкомп’ютери фірм Intel, Fujitsu, Hitachi, Cray-SGI. Одна із останніх розробок Intel об’єднує 9200 процесорів Pentium Pro, займає площу 160 м2 і має масу 40 т. Пристрій для охолодження важить 272 т. Оперативна пам’ять становить 573 ГБ, швидкодія - понад трильйон операцій за секунду. ЕОМ класу міні займають проміжне положення між великими ЕОМ Персональні комп’ютери. Їх можна визначити як комп’ютери, призначені для індивідуального користування. Поділяють їх на настільні
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.012 с.) |

 , більшого одиниці. Нагадаємо, що простим називається число, яке не має дільників, відмінних від одиниці й його самого.
, більшого одиниці. Нагадаємо, що простим називається число, яке не має дільників, відмінних від одиниці й його самого.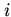 рівним двом і перейти на крок П2.
рівним двом і перейти на крок П2.
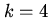

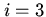
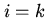 , якщо
, якщо  і дійсних
і дійсних  чисел доводиться працювати з їх замінниками
чисел доводиться працювати з їх замінниками 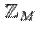 і
і  відповідно. Ці машинні аналоги часто цілком дозволяють забути
відповідно. Ці машинні аналоги часто цілком дозволяють забути
 .
.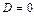 , тоді надрукувати повідомлення «рівняння має один розв’язок:
, тоді надрукувати повідомлення «рівняння має один розв’язок:  ».
». тоді надрукувати повідомлення «рівняння має два корені:
тоді надрукувати повідомлення «рівняння має два корені:  і
і  ».
». ) надрукувати повідомлення «рівняння не має дійсних коренів».
) надрукувати повідомлення «рівняння не має дійсних коренів». , вивести…), предикатні блоки (
, вивести…), предикатні блоки ( ,
,  ) і блок закінчення обробки інформації (кінець). Кожен блок належить певному шляху з початкового блоку в кінцевий. Передачу керування між блоками визначають напрямленими стрілками. Предикатний блок використовують для розгалуження керування (умовної передачі керування). Він функціонує так: якщо предикат, що стоїть в середині ромба, справджується (набуває значення «істина», позначається «і»), то керування передається одному блоку, якщо ж предикат не справджується (набуває значення «хибність», позначається «х»), тоді керування передається іншому блоку.
) і блок закінчення обробки інформації (кінець). Кожен блок належить певному шляху з початкового блоку в кінцевий. Передачу керування між блоками визначають напрямленими стрілками. Предикатний блок використовують для розгалуження керування (умовної передачі керування). Він функціонує так: якщо предикат, що стоїть в середині ромба, справджується (набуває значення «істина», позначається «і»), то керування передається одному блоку, якщо ж предикат не справджується (набуває значення «хибність», позначається «х»), тоді керування передається іншому блоку.
 за допомогою блок-схеми, а потім переведіть блок-схему в програму на Паскалі.
за допомогою блок-схеми, а потім переведіть блок-схему в програму на Паскалі. Команди слід записувати у пристрій запам’ятовування у вигляді машинних «слів», що задають в числовому вигляді. Числа, які машина обробляє, мають бути заданими у вигляді машинних слів. Інакше кажучи, машинні слова задають команди і дані.
Команди слід записувати у пристрій запам’ятовування у вигляді машинних «слів», що задають в числовому вигляді. Числа, які машина обробляє, мають бути заданими у вигляді машинних слів. Інакше кажучи, машинні слова задають команди і дані. Одноадресна і двохадресна машини працюють за іншим принципом.
Одноадресна і двохадресна машини працюють за іншим принципом.  можна описати списком, зображеним на рис. 2.4.
можна описати списком, зображеним на рис. 2.4. Є ще один тип обчислювальних пристроїв, який стоїть трішки виокремлено – це нейрокомп’ютер. З початку створення обчислювальних пристроїв спеціалісти намагалися створити такий пристрій, який би моделював роботу мозку людини. Оскільки в ньому головну роль виконує нейрон, можна знайти ключ до моделювання розумової діяльності людини в моделюванні роботи нейрону мозку. Для багатьох цілей нейрон можна розглядати як елемент з певним критичним значенням. Це означає, що він або ж дає на виході деяку постійну величину, якщо сума його входів досягає певного значення, або ж залишається пасивним.
Є ще один тип обчислювальних пристроїв, який стоїть трішки виокремлено – це нейрокомп’ютер. З початку створення обчислювальних пристроїв спеціалісти намагалися створити такий пристрій, який би моделював роботу мозку людини. Оскільки в ньому головну роль виконує нейрон, можна знайти ключ до моделювання розумової діяльності людини в моделюванні роботи нейрону мозку. Для багатьох цілей нейрон можна розглядати як елемент з певним критичним значенням. Це означає, що він або ж дає на виході деяку постійну величину, якщо сума його входів досягає певного значення, або ж залишається пасивним.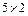 у нас є в пам’яті, і ми кожного разу його не обчислюємо, на противагу комп’ютеру. Існує думка, що процеси мислення є не що інше як розповсюдження певного збудження, як деяка ланцюгова реакція. Навіть найпримітивніші процеси навчання принципово залежать від послідовності подій у часі. Це й закладено в природу нейронних систем. Тому їм притаманне реагування тільки на жорстко визначене зовнішнє подразнення. Наприклад, домашні тварини «навчаються» ігнорувати повторні несуттєві зовнішні подразнення («цокання» годинника), але посилюють сприйняття подразнень, які можуть мати серйозні наслідки (звук гальм автомобіля).
у нас є в пам’яті, і ми кожного разу його не обчислюємо, на противагу комп’ютеру. Існує думка, що процеси мислення є не що інше як розповсюдження певного збудження, як деяка ланцюгова реакція. Навіть найпримітивніші процеси навчання принципово залежать від послідовності подій у часі. Це й закладено в природу нейронних систем. Тому їм притаманне реагування тільки на жорстко визначене зовнішнє подразнення. Наприклад, домашні тварини «навчаються» ігнорувати повторні несуттєві зовнішні подразнення («цокання» годинника), але посилюють сприйняття подразнень, які можуть мати серйозні наслідки (звук гальм автомобіля).


