
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інваріант і функція обмеження циклуСодержание книги
Поиск на нашем сайте
Основна ідея методу проектування циклу за допомогою інваріанту - вираження взаємозв'язку між змінними в тілі циклу об'єктами у вигляді незмінної умови. Користь інваріанта полягає в тому, що такий опис взаємозв'язку легко зрозумілий і дозволяє, знаючи, як змінюються одні об'єкти, виводити, як мають змінюватимуться інші. Тим самим інваріант допомагає сконструювати команди S0 і S.
Для побудови коректної умови продовження циклу e використовується обмежуюча функція h. На кожному кроці циклу значення Визначення 9.7. Обмежуюча функція
Геометрична інтерпретація даної схеми наведена на рисунку 9.2, де через
ЗАВДАННЯ 9.24. Напишіть програму, яка знаходить добуток двох цілих чисел, одне з яких невід'ємне, без використання операції множення. Точні перед- і постумови необхідної програми, часова складність якої не повинна перевершувати
Рішення. Для написання програми треба сконструювати S0 (сукупність присвоєнь, здійснюють початкову ініціалізацію), умову продовження e і тіло циклу S. Початкові присвоювання повинні легко знаходитися та зробити істинним інваріант (у разі істинності передумови) і при цьому залишатися максимально простими. У нашому випадку досить швидко можна виявити, що гарним кандидатом на роль S0 є наступна сукупність присвоювання "x = a; y = b; z = 0;". Умова продовження циклу e нам вже по-суті дана, бо чергова ітерація циклу повинна відбуватися тільки за h > 0. З цієї причини логічно припустити, що наша програма повинна містити оператор "while (y> 0) S;", тіло якого S поки невідомо. Ми зобов'язані забезпечити завершення циклу, отже величина y повинна зменшуватися на кожній його ітерації. Зменшення y щоразу на одиницю свідомо не дозволить одержати досить ефективну програму. З цієї причини необхідно зменшувати величину y більш швидко. Гарною думкою є спроба ділити величину y навпіл тоді, коли це можна (при парних y). Легко оцінити, що якщо б поділ навпіл відбувалося на кожному кроці циклу, то кількість його ітерацій приблизно дорівнювала б log b. Це цілком узгоджується з тим, що потрібно для умови задачі по складності. Враховуючи те, що після ітерації циклу інваріант повинен залишитися істинним, і вже знаючи як змінюється y, обчислюємо, як слід змінювати (бо за умовою задачі ми не можемо змінюват a і b). У результаті знаходимо (або в думках, або формально обчислюючи wp), що при парних y величину x слід подвоювати, а при непарних - необхідно збільшувати значення змінної z на x. Програма написана! Текст програми: public class MulI { public static void main(String[] args) throws Exception { int a = Xterm.inputInt("a -> "); int b = Xterm.inputInt("b -> "); int x = a, y = b, z = 0; while (y > 0) { if ((y&1) == 0) { y >>>= 1; x += x; } else { y -= 1; z += x; } } Xterm.println("a * b = " + z);}
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 — предикат, який правдивий перед виконанням циклу і після кожної його ітерації.
— предикат, який правдивий перед виконанням циклу і після кожної його ітерації. має зменшуватися принаймні на одиницю і залишатися додатнім до кінця циклу. Функція обмеження дозволяє гарантувати завершення циклу.
має зменшуватися принаймні на одиницю і залишатися додатнім до кінця циклу. Функція обмеження дозволяє гарантувати завершення циклу. невід'ємна функція, що є верхньою межею поміж решти ітерацій циклу.
невід'ємна функція, що є верхньою межею поміж решти ітерацій циклу. береться предикат
береться предикат  .
.  позначено множину, що виходить з
позначено множину, що виходить з  за допомогою сукупності присвоювання S0.
за допомогою сукупності присвоювання S0.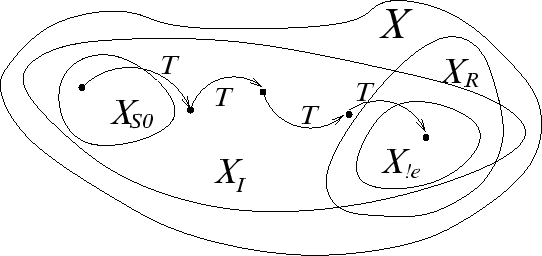
 такі:
такі:  ,
,  . При написанні програми величини
. При написанні програми величини  і
і 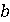 змінювати не дозволяється, слід використовувати інваріант
змінювати не дозволяється, слід використовувати інваріант 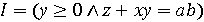 і обмежуючу функція
і обмежуючу функція  .
.


