
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абстрактна семантика процедурних програм.Содержание книги
Поиск на нашем сайте
Кожну програму Р можна розглядати як слово в деякій мові програмування, побудоване за правилами синтаксису цієї мови. Якщо задана інтерпретація (значення) змінних програми Р, то можна говорити про семантику (сенс) даної програми. Побудова синтаксису мови програмування і синтаксично правильного слова (програми Р) в цій мові на сьогодні не складає великої проблеми. А от побудова семантично правильної програми - це одна з основних (якщо не основна) проблема при проектуванні програмної системи. Складність цієї проблеми полягає в тому, що обґрунтування семантики тієї чи іншої мови програмування - це, як правило, вимагає розв’язання не однієї, а декількох складних математичних задач, в зв’язку з можливими інтеграціями парадигм. Дослідження самих парадигм програмування і їх об’єктів дає можливість описати для деяких з них абстрактну семантику, тобто описати семантику незалежно від конкретної мови програмування. Як зазначалося вище, при розгляді процедурної парадигми, будь-яку процедурну програму можна розглядати як структурну, побудова якої (без викликів підпрограм і процедур-функцій) зводиться до композиції таких чотирьох об’єктів:
Виходячи з цього, абстрактний синтаксис процедурної програми можна записати в нормальній формі Бекуса так:
< program >::=< operational-expression >; < operational-expression >::= < operator > | < operational-expression >; < operator >::= < assign > | < sequentional-composition > | < conditional-composition > | < iteration >; < assign >::= < variable >:= < expression >; < variable >::= < element-from-setvariables R >; < expression >::= < term-of-algebra TD(R) >; < sequential-composition >::= (< operator >; < operational-expression >); < conditional-composition >::= if(< condition >,< operational-expression >, < operational-expression >); < iteration >::= while(< condition >, < operational-expression >); < condition >::= < propositional-boolean-function-on
Вираз Семантика програм, незалежно від їх парадигм, має два різновиди: денотаційна семантика і операційна семантика. Як ми вже зазначали цей поділ ґрунтується на тому, що при виконанні будь-якої програми необхідно вміти відповідати на такі два питання: а) що обчислювати? і б) як обчислювати? Відповідь на перше питання повинна давати денотаційна семантика, а відповідь на друге - операційна. Денотаційна семантика. Нехай задані
Множину всіх відображень В з множини R в область даних В позначимо через B= З даною програмою Р зв’яжемо часткову функцію Визначимо: а) семантику виразів:: б) семантику імен виразів:: в) семантику умов:: Виходячи з цього означення і абстрактного синтаксису, денотаційну семантику процедурних програм можна визначити так: 1) P = (x:= y) 2) P = ( 3) P = if(u, 4) P = while(u,Q) де n - найменше натуральне число такe, що для всіх 0 ≤ т < n мають місце умови
Операційна семантика Операційну семантику можна описати як транзиційну систему, тобто як множину станів обчислень і відношення переходів між цими станами. Пару (Р,b), де Р - програма, a b - стан пам’яті, називатимемо станом обчислень. Серед станів обчислень виділимо стан (succ, b) для фіксації успішного завершення обчислень програмою, тобто стан (succ,b) є заключним станом обчислень. Бінарне відношення переходів → на станах обчислень позначається через (P, b) → (Р', b') і знаходиться за такими правилами: а ) (x:=y,b) →(succ,
в ) г ) д ) e ) є ) Таким чином, в результаті розгляду операційної семантики приходимо до поняття історії обчислень, як послідовності станів обчислень (P,b) Ця історія може бути як скінченна, так і нескінченна. Якщо історія скінченна, то її останнім етапом є стан (sucс, b), а стан пам’яті b Є В називається результатом виконання програми Р. Нехай відношення При цьому кожний стан обчислень породжує єдину історію обчислень. Тепер виникає питання, як пов’язані між собою денотаційна і операційна семантики? Відповідь на це питання дає таке твердження. Теорема 3.1.
Доведення виконується методом математичної індукції з розглядом можливих варіантів обчислення функції Розглянемо приклад процедурної програми. Програма обчислення найбільшого спільного дільника двох Процедурна програма, як і функціональна, алгебраїчна і логічна програми обчислення НСД(х, у), де х, у - цілі натуральні числа, ґрунтується па таких властивостях цієї функції. 1. НСД(х,х) = х; 2. х>у ⇒НСД(х, у) =НСД(х -у,у); 3. х < у ⇒ НСД(х, у) =НСД(х, у - х).
Імперативна програма має такий вигляд:
НСД(х ,у). Вхід: х, у Є N. Вихід: d Є N. begin а:= х; b:= у; while а ≠ b do if а > b then а:= а - b else b:= b - a; fi; od; d:= а; End
Структурність і модульність Спочатку процедурне програмування користувалося довільними засобами керування, в тому числі, переходом за міткою — одним з найбільш вживаних операторів керування в Фортрані. Ось приклад програмного тексту з Фортрану C КВАДРАТНИЙ КОРІНЬ З ДІЙСНОГО ЧИСЛА REAL FUCTION ROOT (A) S=A IF (A.EQ.0) GO TO 20 10 T=(S+A/S)*.5 IF (ABS((T-S)/T).LE.1.Е-6) GO TO 20 S=T GO TO 10 20 ROOT=S END В 1968 році голландський вчений Е.Дейкстра вперше звернув увагу на проблеми, що виникають у програмах з неконтрольованими переходами, в 1970 році проголосив новий напрямок, який він назвав структур(ова)ним програмуванням. Структурне програмування — це варіант процедурного, що вживає три типи структур керування: послідовне виконання дій, розгалуження і цикл. Не дивно, що Фортран не підтримував цю парадигму — в наборі його засобів не було циклів за умовами. Починаючи з Алголу, а особливо в Паскалі, цикли стають основним засобом організації обчислень в програмі: function root(a:real,eps:real): real; var s, t: real; begin s:=a*0.5; repeat t:=s; s:=(s+a/s)*O.5; until abs(s-t)/s<eps do root:=s; end Автор Паскалю, професор Н.Вірт, відібрав до створюваної ним мови програмування лише прості в поясненні і легкі в реалізації конструкції. Завдяки сильній типізації програми в Паскалі відзначаються високою надійністю, вони мобільні завдяки закладеній в них концепції Паскаль-машини, їх легко читати і розуміти завдяки дисципліні програмування, продиктованої вжитою парадигмою. Але разом з цим застосування Паскалю гальмувалося саме складністю виходу за межі віртуальної машини, потребою ефективного використання наявної апаратури. Головним критерієм, вжитим Б.Керніганом і Д.Річі до створеної ними мови С, стала саме гнучкість використання особливостей конкретної апаратури і ефективність виконання програм. Модульне програмування Процедурна парадигма віддала належне алгоритмічній компоненті програмування. Але з ростом обсягу програм і складності даних з’явилася нова проблема структурної організації даних, найбільш ємко висловлена віртовською формулою “алгоритми + структури даних = програми”. Поняття модуля як абстракції даних було вперше запропоноване Парнасом у 1972 році, правда на той час уже існувала мова програмування Симула 67, в якій використовувалася парадигма об’єктів. У найбільш повному виді поняття абстракції даних було реалізоване в мові програмування Модула-2. Головна ідея полягає в забезпеченні доступу до даних, не залежному від їх конкретного представлення. Самі дані і програми їх обробки вбудовуються (інкапсулюються) в окремій одиниці програми. Ось простий приклад, який показує, як складність обчислень може перетікати у складність даних: обчислення математичної функції, скажімо, квадратного кореня, можна виконати, обчислюючи границю відповідної послідовності, наприклад такої: Цей же квадратний корінь можна знайти у відповідному рядку чотиризначних математичних таблиць Брадіса. У першому випадку вся складність зосереджена в алгоритмі, який необхідно було придумати і запрограмувати (що ми й зробили у наведеному вище прикладі програми на Паскалі). У другому — в структурах даних, тобто в таблицях, які професор В.М.Брадіс повинен був попередньо розрахувати. Ось приклад тексту в Модулі 2, який дає певне уявлення про поділ модуля на дві частини — визначення і реалізацію: definition module Months; type Month= (jan, feb, mch, apr, may, jun, jul, aug, sep, oct, nov, dec);
procedure length(m: Month): Cardinal; end Month;
implementation module Month; var len: array Month of Cardinal; procedure length(m: Month): Cardinal; begin return len[m]; end length;
begin len[jan]:=31; len[feb]:=28; len[mch]:=31; len[apr]:=30; len[may]:=31; len[jun]:=30; len[jul]:=31; len[aug]:=31; len[sep]:=30; len[oct]:=31; len[nov]:=30; len[dec]:=31; end Month.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.012 с.) |

 (R) >.
(R) >. і будемо називати множиною станів пам’яті або інформаційним середовищем.
і будемо називати множиною станів пам’яті або інформаційним середовищем. : В → B, яка повинна обчислюватись цією програмою. Значення функції
: В → B, яка повинна обчислюватись цією програмою. Значення функції  (b) на стані пам’яті b Є В будемо позначати через
(b) на стані пам’яті b Є В будемо позначати через  : В → R, де х - змінна;
: В → R, де х - змінна; : В → {0,1}, де и - умова.
: В → {0,1}, де и - умова.
 (b)(r) =
(b)(r) = 
 ))
))  (
(  ;
;
 );
); (b)),
(b)), Більш лаконічно цe можна записати у вигляді рекурсивного означення:
Більш лаконічно цe можна записати у вигляді рекурсивного означення: = 0, b,
= 0, b,  ).
). );
); ;
;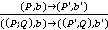 , де
, де 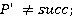
 ;
;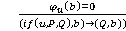 ;
; ;
; .
. (
( )
)  )
)  …
… * означає рефлексивно-транзитивне замикання відношення переходів
* означає рефлексивно-транзитивне замикання відношення переходів 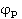 (b) = b' ⇔ (P,b)
(b) = b' ⇔ (P,b)  (b) (пункти 1) - 4)) і відношення
(b) (пункти 1) - 4)) і відношення 



