
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметичні і побітові оператори мови JavaСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Будь-який оператор з привласненням з точки зору одержуваного результату еквівалентний виконання відповідної операції з подальшим привласненням, але працює зазвичай швидше: @ = B еквівалентно а = @ B (тут символ @ означає будь-яку з бінарних арифметичних операцій). Результат виконання операцій ділення і ділення за модулем (знаходження залишку) для цілочисельних операндів є цілим числом. Так, наприклад, 5/3 дорівнює 1. int i = 2, j = 3; // i = 2, j = 3 int k = i + j++; // k = 5, j = 4 int m = --i; // i = 1, m = 1
Таблиця 6: Бітові операції
Наприклад, 4 ~ 5 дорівнює 1 (бо виконавчі подання цих чисел є відповідно 100 і 101).
Задачи для самостійного рішення
Розділ II. Проектування програм з використанням мови програмування Java
Представлення інформації у комп'ютері
Будь-яка інформація (числова, текстова, звукова, графічна тощо) в комп'ютері представляється (кодується) у так званій двійковій формі. Як оперативна, так і зовнішня пам'ять, де і зберігається вся інформація, можуть розглядатися, як досить довгі послідовності з нулів і одиниць. Під зовнішньою пам'яттю маються на увазі такі носії інформації, як магнітні і оптичні диски, стрічки і т.п. Одиницею виміру інформації є біт (BInary digiT) - саме таку кількість інформації міститься у відповіді на питання: нуль чи один? Більшими одиницями виміру інформації є байт, кілобайт (Kbyte), мегабайт (Mbyte), гігабайт (Gbyte) і терабайт (Tbyte). Один байт (byte) складається з восьми біт, а кожна наступна величина більша від попередньої в 1024 рази. Байта достатньо для зберігання 256 різних значень, що дозволяє розміщувати в ньому будь-який з алфавітно-цифрових символів, якщо тільки ми можемо обмежитися мовами з невеликими алфавітами типу української чи англійської. Перші 128 символів (займають семеро молодших біт) стандартизовані за допомогою кодування ASCII (American Standart Code for Information Interchange). Гірше йде справа з кодуваннями українського тексту (символи українського алфавіту розташовані у другій половині таблиці з 256 символів) - їх кілька, а найбільш поширені з них зараз дві - Windows-1251 і KOI8-R. Для кодування всіх можливих символів, використовуваних народами світу, одного байта мало - необхідно використовувати два послідовних (стандарт Unicode). Саме так і роблять при зберіганні символьних (char) значень в мові Java. Корисно знати: що в книзі середнього розміру близько 300000 букв, легко підрахувати, що навіть не використовуючи ніяких ресурсів стиснення інформації, на жорсткому диску сучасного персонального комп'ютера ємністю в 20 гігабайт можна розмістити велику бібліотеку з майже 70000 книг. Цілі числа До цілочисельних типів в мовах програмування традиційно відносяться byte, short, int і long. Для збереження значень цих типів на будь-якому комп'ютері відводиться один, два, чотири і вісім байт відповідно. Застосовується представлення чисел в так званому двійковому додатковому коді. Нагадаємо, що використовувана нами звичайна система числення є позиційною з основою 10. Це означає, що в ній всі натуральні числа представляються за допомогою десяти цифр (від нуля до дев'яти включно), а значення кожної з цифр числа залежить від позиції: перша права цифра означає число одиниць ( У р-ічній системі числення все точно так, як з числом 10 в попередньому абзаці лише потрібно всюди замінити 10 на р. Поряд з двійковою системою, в якій тільки дві цифри (0 і 1), в інформатиці часто застосовуються вісімкова з цифрами від нуля до 7 і шістнадцяткова. В останньому випадку в якості цифр від десяти до п'ятнадцяти використовуються букви від A до F відповідно. При записі позитивних (додатніх) цілих чисел у системі числення з основою р (на комп'ютері p=2) всі їх множини виявляється складаються з елементів виду
де величини Перейдемо тепер до питання представлення негативних (відємних) чисел. Для визначеності розглянемо тип byte, в якому будь-яке число займає рівно вісім біт. Із запису в двійковій системі числення рівності xxxxxxxx + 00000001 = 00000000. Ясно, що на місці символів xxxxxxxx повинно бути розташоване число 11111111. Правильним результатом при цьому, звичайно, слід було б вважати 100000000, а не 00000000, але ж ми маємо справу з типом byte і, так як результат зобов'язаний розміститися в байті, одиниця зникає. Отже, число Негативні числа завжди мають у своєму двійковому поданні одиницю в найстаршому розряді, який тому називають знаковим, а абсолютна величина кодованого числа виходить як двійкове доповнення інших біт (нулі потрібно замінити на одиниці і навпаки), збільшена на один. Легко бачити, що при цьому найменшим негативним числом, яке належить типу byte, є число Цікавим є наступне спостереження: якщо число 01111111 збільшити на одиницю, то вийде 10000000, що означає наступне: Отже, множину елементів типу byte можна уявляти собі у вигляді згорнутого в кільце відрізка Те, що для елементів множини Дійсні числа Для представлення дійсних чисел в мовах програмування традиційно використовують змінні і константи типів float і double. Величини першого з них займають чотири байти, а другого - вісім. На відміну від множини цілих чисел Найбільш поширеним способом реалізації дійсних чисел на ЕОМ є використання чисел з плаваючою крапкою. У цьому випадку множина
У цьому випадку число Число У мові Java для кодування величин типів float і double також використовують числа з плаваючою крапкою. При цьому частину з наявної множини біт використовують для розміщення експоненти e, а інші біти - для розміщення мантиси. Для того щоб добре зрозуміти, що ж представляє з себе множина Тому, що Це число для типів float і double визначено, як MIN_VALUE в класах java.lang.Float і java.lang.Double відповідно. Правіше розташовується множина точок, наступних один за одним із кроком Окрім перерахованих (і симетричних їм негативних) значень у результаті виконання деяких операцій можуть вийти також такі особливі значення: плюс нескінченність (POSITIVE_INFINITY ), мінус нескінченність (NEGATIVE_INFINITY), мінус нуль і не число (NaN). Наприклад, при поділі одиниці на мінус нуль виходить мінус нескінченність. Описані особливості множин машинних дійсних чисел
ЗАВДАННЯ 7.1. Знайдіть дійсне (типу double) число x таке, що x+1 = x, a (x Розв’язок завдання представляє наступна програма: public class DblMaxVal { public static void main(String[] args) { double x = Double.MAX_VALUE; double y = x + 1.0; if (x == y) { Xterm.print("Для числа "); Xterm.print("x = " + x, Xterm.Blue); Xterm.print(" величини x и (x+1) "); Xterm.print("рівні!\n", Xterm.Red); } y = 2.0 * x; double z = y / 2.0; if (x!= z) { Xterm.print("Для числа "); Xterm.print("x = " + x, Xterm.Blue); Xterm.print(" величини x и (2.0*x)/2.0 "); Xterm.print("різні\n", Xterm.Red); Xterm.print("і рівні відповідно"); Xterm.print(" " + x, Xterm.Red); Xterm.print(" і"); Xterm.print(" " + z + "\n", Xterm.Red); } }} ЗАВДАННЯ 7.2. Знайдіть такі дійсні (типу doubie) числа a, b і c такі, що a+(b+c) Розв’язок завдання представляє наступна програма: public class DblNoAssociative { public static void main(String[] args) { double x = 1.0e-16; double y = 1. + (x + x); double z = (1. + x) + x; if (y!= z) { Xterm.print("Для числа "); Xterm.print("x = " + x, Xterm.Blue); Xterm.print(" величини 1.+(x+x) и (1.+x)+x "); Xterm.print("різні\n", Xterm.Red); Xterm.print("і рівні відповідно"); Xterm.print(" " + y, Xterm.Red); Xterm.print("і"); Xterm.print(" " + z + "\n", Xterm.Red); } }}Інколи навіть робота з не дуже малими або великими за абсолютною величиною числами може призвести до незвичайних результатів. Поглянемо на задачу про розв’язок квадратного рівняння. ЗАВДАННЯ 7.3. Напишіть програму, яка вводить дійсні коефіцієнти a, b і c квадратного рівняння
Ось найпростіше розв’язання цієї задачі, яке може бути написане будь-ким, хто має мінімальні знання мови Java.
Для визначення квадратного кореня тут використовується метод sqrt класу Math. Виклик методу System.exit і застосування оператора return, які в тілі методу main майже еквівалентні і приводять до негайного завершення виконання програми, що дозволяє обійтися без гілки else оператора if-else. Інша частина програми коментарів не потребує.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 , а зрушення вправо - поділу на те ж число.
, а зрушення вправо - поділу на те ж число. ), друга - десятків (
), друга - десятків ( ), третя - - сотень (
), третя - - сотень ( ) і так далі.
) і так далі.
 для всіх i з діапазону від
для всіх i з діапазону від  до нуля - це цифри
до нуля - це цифри  -значного числа
-значного числа  з р-цяткової системи числення.
з р-цяткової системи числення. легко знайти, який вигляд повинен мати невідоме нам поки двійкове подання xxxxxxxx числа
легко знайти, який вигляд повинен мати невідоме нам поки двійкове подання xxxxxxxx числа  :
: зменшити на одиницю, що дасть 11111110; число
зменшити на одиницю, що дасть 11111110; число  представляється як 11111101 і т.д.
представляється як 11111101 і т.д. (двійкове подання 10000000), а найбільшим - число 127 (подання 01111111). Всі представимі (допустимі) числа (а їх 256) в даному випадку можуть бути отримані як перетин двох множин: множини всіх цілих чисел і відрізка
(двійкове подання 10000000), а найбільшим - число 127 (подання 01111111). Всі представимі (допустимі) числа (а їх 256) в даному випадку можуть бути отримані як перетин двох множин: множини всіх цілих чисел і відрізка  .
.
 -128, 127 ]. Принципово нічого не міняється й для типів short, int і long - збільшується тільки довжина відрізка, який вирізається з дійсної прямої перед згортанням його в кільце. Мінімальні і максимальні представлені значення для кожного з цих типів в мовах програмування традиційно визначаються додатково. Наприклад в Java вони визначені, як значення констант MIN_VALUE і MAX_VALUE в класах java.lang.Short, java.lang.Integer і java.lang.Long відповідно.
-128, 127 ]. Принципово нічого не міняється й для типів short, int і long - збільшується тільки довжина відрізка, який вирізається з дійсної прямої перед згортанням його в кільце. Мінімальні і максимальні представлені значення для кожного з цих типів в мовах програмування традиційно визначаються додатково. Наприклад в Java вони визначені, як значення констант MIN_VALUE і MAX_VALUE в класах java.lang.Short, java.lang.Integer і java.lang.Long відповідно. , що є машинним аналогом
, що є машинним аналогом  , порушено фундаментальну властивість цілих чисел
, порушено фундаментальну властивість цілих чисел  , може призвести до різних непередбачуваних на перший погляд результатів, проте набагато більш дивні речі відбуваються за роботи з дійсними числами.
, може призвести до різних непередбачуваних на перший погляд результатів, проте набагато більш дивні речі відбуваються за роботи з дійсними числами. мають властивість щільності (повноти): між будь-якими двома різними числами завжди знайдеться відмінне від них третє. Зрозуміло, що будь-який із способів подання нескінченної кількості дійсних чисел за допомогою деякої обмеженої множини
мають властивість щільності (повноти): між будь-якими двома різними числами завжди знайдеться відмінне від них третє. Зрозуміло, що будь-який із способів подання нескінченної кількості дійсних чисел за допомогою деякої обмеженої множини 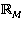 не дасть можливості зберегти властивість щільності.
не дасть можливості зберегти властивість щільності. )
)  , де цілі числа
, де цілі числа  для всіх
для всіх  з діапазону від 1 до
з діапазону від 1 до  задовольняють співвідношення
задовольняють співвідношення 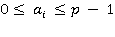 , а величина лежить в діапазоні від
, а величина лежить в діапазоні від  до U (
до U ( ).
).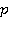 є при цьому основою системи числення (найчастіше це 2), константа n задає точність представлення чисел (для типу double вона більше, ніж для float), а діапазон [ L,U ] визначає область значень експоненти (для типу double він також більше, ніж для float).
є при цьому основою системи числення (найчастіше це 2), константа n задає точність представлення чисел (для типу double вона більше, ніж для float), а діапазон [ L,U ] визначає область значень експоненти (для типу double він також більше, ніж для float).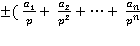 ) прийнято називати мантисою числа f з плаваючою точкою. Часто вимагають, щоб для всіх чисел f
) прийнято називати мантисою числа f з плаваючою точкою. Часто вимагають, щоб для всіх чисел f  величина
величина  була ненульовою. Такі числа з плаваючою точкою називають нормалізованими.
була ненульовою. Такі числа з плаваючою точкою називають нормалізованими. = L,
= L, . Потім крок збільшується. Потім ще. І ще. При
. Потім крок збільшується. Потім ще. І ще. При 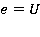 відстань між двома сусідніми точками множини і
відстань між двома сусідніми точками множини і 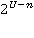 . Найправіша точка множини виходить при
. Найправіша точка множини виходить при  і e =U. Для типів float і double це число визначено, як MAX_VALUE в класах java.lang.Float і java.lang.Double.
і e =U. Для типів float і double це число визначено, як MAX_VALUE в класах java.lang.Float і java.lang.Double.

 існує;
існує;  2 = x;
2 = x;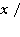 2)
2)  2 = x;
2 = x; •;
•;
 ) / 2
) / 2  x. Скористайтеся тим, що java. lang. Double визначає константу MAX_VALUE.
x. Скористайтеся тим, що java. lang. Double визначає константу MAX_VALUE. (a +b) + c. Достатньо згадати, що точки множини
(a +b) + c. Достатньо згадати, що точки множини  знаходяться на числовій прямій нерівномірно.
знаходяться на числовій прямій нерівномірно.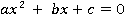 з позитивним дискримінантом, що знаходить обидва корені цього рівняння.
з позитивним дискримінантом, що знаходить обидва корені цього рівняння. + bx + c, то і для x1 x2 і для його значення виявиться рівним одиниці, а не нулю. Подібна помилка для першого, досить великого за величиною кореня, видається цілком природною, але ось погоджуватися з тим, що нуль є коренем даного рівняння, зовсім не хочеться. Цій проблемі присвячена одна з наведених нижче задач.
+ bx + c, то і для x1 x2 і для його значення виявиться рівним одиниці, а не нулю. Подібна помилка для першого, досить великого за величиною кореня, видається цілком природною, але ось погоджуватися з тим, що нуль є коренем даного рівняння, зовсім не хочеться. Цій проблемі присвячена одна з наведених нижче задач.


