Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування теорії індуктивних функційСодержание книги
Поиск на нашем сайте
Як перший приклад розглянемо задачу котра вже траплялася нам раніше. Задача 10.1. Напишіть програму, що вводить послідовність цілих чисел, і друкує кількість її максимальних елементів. Розв’язок. В даній задачі Для побудови її індуктивного розширення F застосуємо стандартний прийом. Спробуємо визначити значення функції маємо
Ми бачимо, що у якості
Ця функція, проте, не визначена на пустому ланцюжку, тому
Відображення
то побудоване нами розширення виявиться мінімальним. Тепер можна написати програму, що реалізовує побудований алгоритм. Текст програми. public class NumMaxSeq2 { public static void main(String[] args) { int y1 = 0, y2 = Integer.MIN_VALUE; try { while (true) { int x = Xterm.inputInt("x -> "); if (x == y2) { y1 += 1; } else if(x > y2) { y1 = 1; y2 = x; } } } catch (Exception e) { Xterm.println("\nn = " + y1); } }}Будь-яка помилка при введенні розглядається тут, як завершення послідовності чисел. Імена змінних, наявних в програмі, збігаються з використаними при побудові алгоритму, обчислення Задача 10.2. Напишіть програму, яка визначає номер Рішення. Маємо Побудуємо її індуктивне розширення
отже, в якості
Помітимо, що всі значення функції Побудоване нами розширення мінімальним не являється, оскільки значення (1,0) не може бути набуте функцією Ось програма, що не використовує наявності стаціонарних значень. Текст програми. public class First1{ public static void main(String[] args) throws Exception { int x0 = Xterm.inputInt("x0 ->"); int y1 = 0, y2 = 0; try { while (true) { int x = Xterm.inputInt("x -> "); y2 += 1; if ((y1 == 0) && (x == x0)) y1 = y2; } } catch (Exception e) { Xterm.println("\nn = " + y1); } }}Імена програмних змінних співпадають з використаними при побудові алгоритму, обчислення Програма, що використовує наявність у функції Текст програми. public class First2 { public static void main(String[] args) throws Exception { int x0 = Xterm.inputInt("x0 -> "); int y1 = 0, y2 = 0; try { while (y1 == 0) { int x = Xterm.inputInt("x -> "); y2 += 1; if (x == x0) y1 = y2; } } catch(Exception e){ System.exit(0); } Xterm.println("\nn = " + y1); }}По досягненню кінця послідовності, що вводиться, ця програма не виконує ніяких спеціальних дій (оператор ";" у блоці "catch"). У цій ситуації, як і у разі прийняття функцією Задача 10.3. Напишіть програму, яка вводить послідовність дійсних чисел, та друкує середне арифметичне її елементів (для не порожньої послідовності). Рішення. За умовою завдання Побудуємо її індуктивне разширення Отже, у якості Проектована програма буде простіша, якщо ми зможемо продовжити то з останньої рівності отримуємо Текст програми. public class AverSeq{ public static void main(String[] args) { double y1 = 0., y2 = 0.; try { while (true) { double x = Xterm.inputDouble("x -> "); y1 = (y1*y2 + x) / (y2 + 1.); y2 += 1; } } catch(Exception e) { Xterm.println("\nf = " + y1); } }}Розглянемо завдання дещо іншого типу. Задача 10.4. Напишіть програму, яка визначає кількість входжень взірця Рішення. Нехай Помітивши, що
Введемо додаткову функцію
Необхідно ввести ще одну додаткову функцію
Оскільки нам знову не вдалося виразити
Отримана рівність показує, що
Зараз ми доведемо, що функція Для доказу індуктивності досить показати перетворення
Для доказу сюр’єктивності функції Хай Текст програми. import java.io.*;public class ABCDSeq { public static void main(String[] args) { DataInputStream in = new DataInputStream(System.in); int f = 0, n = 0; try { while (true) { char x = (char)in.readByte(); if (x=='\n') continue; if (x=='d' && n==3) { f += 1; n = 0; } else if (x=='c' && n==2) { n = 3; } else if (x=='b' && n==1) { n = 2; } else if (x=='a') { n = 1; } else{ n = 0; } } } catch(Exception e) { Xterm.println("f = " + f); } }}У цій програмі використовується метод "readByte", який дозволяє вводити символи. При цьому символ '\n' також виявляється введеним після того, як користувач натискає клавішу Enter на клавіатурі. Цей символ необхідно ігнорувати, що і реалізується в програмі оператором "if (x=='\n') continue". Не використані нами раніше оператори "import java.io.*" та "DataInputStream in = new DataInputStream (System.in) " потрібні для виклику методу "readByte". У всьому іншому програма повністю відповідає проведеному перед її побудовою дослідженню. Завдання для самостійного вирішення При вирішенні завдань, наведених нижче, необхідно з'ясувати, чи є індуктивної задана функція Задача 10.5. Напишіть програму, яка визначає кількість мінімальних елементів у послідовності непозитивних цілих чисел. Вказівіка. В даному випадку для довизначення індуктивного розширення на порожньому ланцюжку немає необхідності використовувати величини Integer MIN_VALUE або Integer MAX_VALUE. Задача 10.6. Напишіть програму, яка визначає значення в цілій точці Задача 10.7. Напишіть програму, яка визначає значення у цілій точці Вказівка. Продиференцирував по Завдання 10.8. Напишіть програму, що визначає правильність формули над алфавітом з чотирьох символів ВКАЗІВКА. Розгляньте наступне індуктивне розширення
Задача 10.9. Напишіть програму яка визначає номер
Джерела
1. Глибовець М. М. Основи комп’ютерних алгоритмів. Монографія, Київ: Видавничий дім “КМ Академія”, 2003. – С. 452. 2. Глибовець М. М., Глибовець А.М., Проценко В.С. Практикум з мови програмування Сі. Навчальний посібник, Київ, Видавничий дім “КМ Академія”, 2010. - с.365. 3. Кушниренко А.Г., Лебедев Г.В. Программирование для математиков. -- М., Наука, 1988 4. Ахо А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы. -- M.: Изд. дом <<Вильямс>>, 2000. 5. Бадд Т. Об’єктно-ориентированное программирование в действии. -- СПб.: Питер Паблишинг, 1997. 6. Вирт Н. Алгоритмы + структуры данных = программы. -- М.: Мир, 1985. 7. Грис Д. Наука программирования. -- М.: Мир, 1984. 8. Роганов Е.А. Основі інформатики и программирования. –М.: МГИУ, 2001.–315с. 9. Кнут Д. Искусство программирования, 3-е изд., Т.1. Основные алгоритмы. -- M.: Изд. дом <<Вильямс>>, 2000. 10. Кнут Д. Искусство программирования, 3-е изд., Т.2. Получисленные алгоритмы. -- M.: Изд. дом <<Вильямс>>, 2000. 11. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. -- M.: МЦНМО, 2000.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

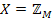 ,
, 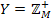 ,
, 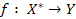 . Взявши a=1, b=2, x =2, знаходимо
. Взявши a=1, b=2, x =2, знаходимо 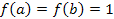 , але
, але 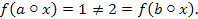 Із заперечення критерію індуктивності робимо висновок, що
Із заперечення критерію індуктивності робимо висновок, що 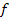 не є індуктивною.
не є індуктивною. на подовженому ланцюгу через її значення
на подовженому ланцюгу через її значення 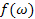 на вихідній і елемент
на вихідній і елемент  . Відомо, що це неможливо зробити (
. Відомо, що це неможливо зробити ( . Розглянемо тепер функцію
. Розглянемо тепер функцію 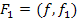 . В тому випадку, якщо вона індуктивна, потрібне розширення побудоване. Інакше повторимо попередні дії і спробуємо виразити
. В тому випадку, якщо вона індуктивна, потрібне розширення побудоване. Інакше повторимо попередні дії і спробуємо виразити  через
через 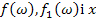 з використанням додаткової інформації
з використанням додаткової інформації 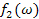 . Отримуємо наступного кандидата на роль індуктивного розширення – функцію
. Отримуємо наступного кандидата на роль індуктивного розширення – функцію 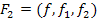 . При необхідності даний процес може бути продовжений і далі, а його завершення гарантується теоремою про існування індуктивного розширення. В даному випадку.
. При необхідності даний процес може бути продовжений і далі, а його завершення гарантується теоремою про існування індуктивного розширення. В даному випадку.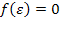 ,
,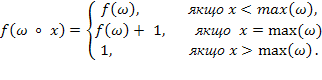
 необхідно взяти функцію
необхідно взяти функцію  , яка обчислює максимальне значення елементів на ланцюжку. Тоді для
, яка обчислює максимальне значення елементів на ланцюжку. Тоді для  отримуємо
отримуємо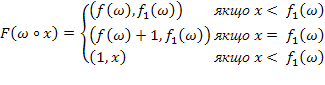
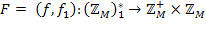 також визначна тільки на
також визначна тільки на 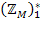 . Скориставшись тим, що діапазон представлення цілих чисел на ЕОМ обмежений, в даному випадку можна до визначити F зі збереженням функції переобчислення наступним чином:
. Скориставшись тим, що діапазон представлення цілих чисел на ЕОМ обмежений, в даному випадку можна до визначити F зі збереженням функції переобчислення наступним чином: 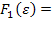 Integer.MIN_VALUE (
Integer.MIN_VALUE (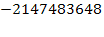 для мови Java). Дійсно, якщо припустити, що найбільшим елементом на порожньому ланцюжку являється представлене мінімальне на ЕОМ ціле число, то
для мови Java). Дійсно, якщо припустити, що найбільшим елементом на порожньому ланцюжку являється представлене мінімальне на ЕОМ ціле число, то 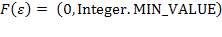 , а функція
, а функція 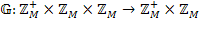 визначається формулою
визначається формулою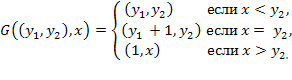
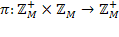 тривіально:
тривіально: 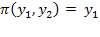 . Доведемо, що побудоване нами розширення
. Доведемо, що побудоване нами розширення 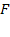 не являється мінімальним. Для цього достатньо пред'явити значення
не являється мінімальним. Для цього достатньо пред'явити значення  , яке не приймається взагалі на жодному ланцюжку. Таким буде, наприклад,
, яке не приймається взагалі на жодному ланцюжку. Таким буде, наприклад, 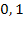 . Доведемо самостійно, що якщо замість простору
. Доведемо самостійно, що якщо замість простору 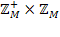 розглянути
розглянути ,
,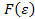 виконується за допомогою команд "int y1 = 0, y2 = Integer.MIN_VALUE;", функція G реалізована за допомогою оператора if - else, в якому опущений випадок
виконується за допомогою команд "int y1 = 0, y2 = Integer.MIN_VALUE;", функція G реалізована за допомогою оператора if - else, в якому опущений випадок 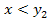 (так як тоді не потрібно змінювати ні
(так як тоді не потрібно змінювати ні 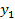 , ні
, ні  ), а застосування відображення
), а застосування відображення 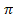 зводиться до друку тільки значення
зводиться до друку тільки значення 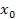 , у послідовності цілих чисел. В тому випадку, якщо число
, у послідовності цілих чисел. В тому випадку, якщо число 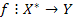 , де
, де 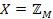 , а
, а 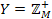 . Якщо
. Якщо 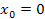 ,
,  ,
, 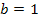 , то
, то 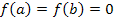 , але
, але 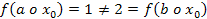 , отже
, отже 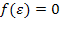 ,
,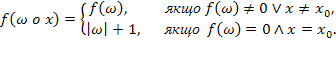
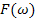 можно узяти пару
можно узяти пару 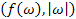 , де функція
, де функція  . Ця функція вже індуктивна, оскільки
. Ця функція вже індуктивна, оскільки 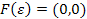 , а перетворення
, а перетворення 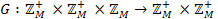 має вигляд
має вигляд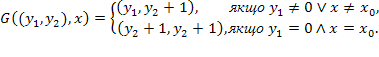
 , відмінні від нуля, є стаціонарними, тоді як функція не має стаціонарних значень. Зрозуміло, що відображення
, відмінні від нуля, є стаціонарними, тоді як функція не має стаціонарних значень. Зрозуміло, що відображення 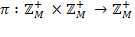 має вигляд.
має вигляд. 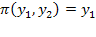
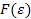 виконується за допомогою команд "int y1=0, y2=0;", реалізація функції
виконується за допомогою команд "int y1=0, y2=0;", реалізація функції  очевидна, а застосування відображення
очевидна, а застосування відображення  зводиться до друку тільки значення
зводиться до друку тільки значення 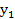 .
.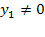 ), управління просто передається на оператор друку. Вирішимо ще одне завдання.
), управління просто передається на оператор друку. Вирішимо ще одне завдання.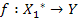 , де
, де 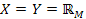 . Якщо
. Якщо  ,
, 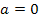 ,
, 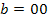 (ланцюжок з двох нулів), то
(ланцюжок з двох нулів), то 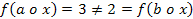 , отже
, отже 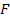 . Позначивши через
. Позначивши через 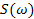 суму елементів послідовності
суму елементів послідовності 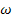 , отримуємо
, отримуємо 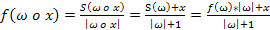 .
. , де
, де 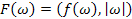 , перетворення
, перетворення 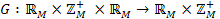 задається формулою
задається формулою  .
. зі збереженням
зі збереженням 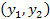 таку, щоб
таку, щоб 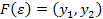 та
та  . Оскільки,
. Оскільки, 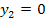
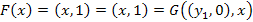 , що правдиво за усіх
, що правдиво за усіх 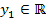 . Отже, можна покласти, наприклад
. Отже, можна покласти, наприклад 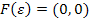 . Тепер
. Тепер  . Відображення
. Відображення  тривіальне:
тривіальне: 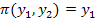 , а побудоване нами розширення не являється мінімальним, оскільки значення функцією
, а побудоване нами розширення не являється мінімальним, оскільки значення функцією 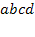 у послідовність символів.
у послідовність символів.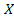 - безліч усіх символів, тоді функція
- безліч усіх символів, тоді функція  . Якщо
. Якщо 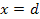 ,
, 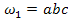 ,
,  , то
, то  , але
, але 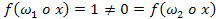 , отже
, отже  , будуватимемо її індуктивне розширення.
, будуватимемо її індуктивне розширення.
 , яка буде істинна тільки тоді, коли
, яка буде істинна тільки тоді, коли 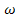 закінчується на
закінчується на 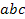 , і розглянемо функцію
, і розглянемо функцію  ,
,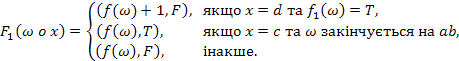
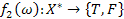 , яка буде істинною тільки тоді, коли
, яка буде істинною тільки тоді, коли 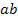 . Тепер можна розглянути
. Тепер можна розглянути 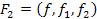 . Для неї маємо
. Для неї маємо 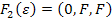 ,
,
 тільки через
тільки через 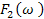 та
та  , доведеться розглянути ще одну функцію
, доведеться розглянути ще одну функцію 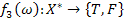 , яка буде істинною тільки тоді, коли
, яка буде істинною тільки тоді, коли 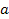 . Для функції
. Для функції 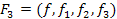 , яка діє у простір
, яка діє у простір 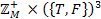 отримуємо
отримуємо 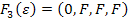 ,
,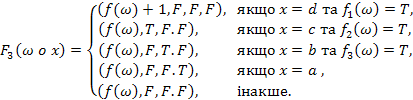
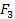 - індуктивне розширення
- індуктивне розширення  і
і 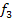 не являються незалежними. У трійки величин
не являються незалежними. У трійки величин 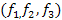 є всього чотири допустимі стани, які можна позначити одним числом
є всього чотири допустимі стани, які можна позначити одним числом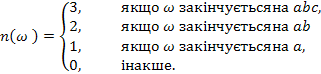
 , яка визначена співвідношенням
, яка визначена співвідношенням 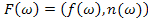 є мінімальним індуктивним розширенням
є мінімальним індуктивним розширенням 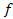 .
.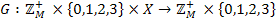 :
: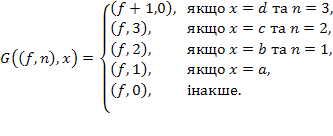
 . Їм може служити, наприклад, ланцюжок, що розпочинається з
. Їм може служити, наприклад, ланцюжок, що розпочинається з 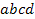 , за яким слідує ще
, за яким слідує ще  перших символів цього зразка. Для того, щоб перевірити другу умову критерію мінімальності, необхідно переконатися в тому, що
перших символів цього зразка. Для того, щоб перевірити другу умову критерію мінімальності, необхідно переконатися в тому, що 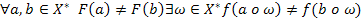 .
.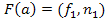 ,
, 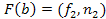 і або
і або 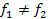 , або
, або  . Якщо
. Якщо  . Ланцюжок
. Ланцюжок 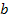 закінчується на
закінчується на 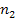 перших символу зразка
перших символу зразка  останніх символу цього зразку, то
останніх символу цього зразку, то  +1
+1  , що і завершує доведення мінімальності
, що і завершує доведення мінімальності 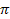 і досліджувати побудоване розширення на мінімальність (мінімальність не являється обов'язковою умовою). Завершити рішення слід написанням програми, що реалізовує однопрохідний алгоритм, із зазначенням відповідності між програмними змінними та позначеннями, використаними в теоретичній частині рішення. Необхідно пояснити, як у програмі реалізується обчислення
і досліджувати побудоване розширення на мінімальність (мінімальність не являється обов'язковою умовою). Завершити рішення слід написанням програми, що реалізовує однопрохідний алгоритм, із зазначенням відповідності між програмними змінними та позначеннями, використаними в теоретичній частині рішення. Необхідно пояснити, як у програмі реалізується обчислення 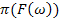 у разі використання індуктивного розширення.
у разі використання індуктивного розширення. багаточлена, який заданий послідовністю його цілих коефіцієнтів (у порядку зростання ступенів).
багаточлена, який заданий послідовністю його цілих коефіцієнтів (у порядку зростання ступенів). та підставив потім
та підставив потім  отримаєте співвідношення
отримаєте співвідношення  ,
,  які допоможуть побудувати індуктивне розширення вихідної функції.
які допоможуть побудувати індуктивне розширення вихідної функції.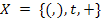 . Формула вважається правильною, якщо вона може бути отримана за допомогою наступної НФБН:
. Формула вважається правильною, якщо вона може бути отримана за допомогою наступної НФБН: 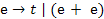 .
.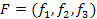 функції f, де
функції f, де 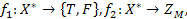
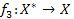 визначені наступним чином:
визначені наступним чином: = може бути продовжена до правильної формули,
= може бути продовжена до правильної формули, = різниця числа лівих і правих дужок у
= різниця числа лівих і правих дужок у  = останній елемент
= останній елемент  у послідовності цілих чисел. У тому випадку якщо число
у послідовності цілих чисел. У тому випадку якщо число