
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тестування і верифікація програмСодержание книги
Поиск на нашем сайте
Всі знають, що в програмах бувають помилки (bugs). Існують спеціальні теорії, присвячені тому, як краще їх знаходити і виправляти (debugging дослівно означає <<виведення клопів>>). Найчастіше знаходження помилки - дуже нетривіальне завдання, так як її наслідки можуть позначатися зовсім в іншому місці програми і бути досить несподіваними. При цьому часто забувається той очевидний факт, що помилку набагато легше запобігти при написанні програми, ніж знайти і виправити потім. Існують методи проектування програм (принаймні, невеликих), що дозволяють не тільки написати правильну програму, але й отримати одночасно з цим абсолютно строге доведення її правильності. Вивченню таких методів і буде присвячена в основному друга частина наших лекцій. Однак для того, щоб вивчити будь-яку теорію, необхідно вивчити мову, на якому теорія може бути викладена. Мова предикатів – це саме та мова, на якому можна строго сформулювати постановку задачі і довести правильність конкретної програми. Спробуйте вирішити наступне завдання.
Задача 1.2. Задача про банку з зернятами кофе. У банці знаходяться декілька чорних і білих зернят кофе. Повторіть наступні дії поки це буде можливо: · Випадково виберіть із банки два зернята і o Якщо вони одного кольору, відкиньте їх, але положіть у банку нове чорне зернятко (зернят поза банкою достатньо); o Якщо вони різного кольору, поверніть у банку взяте біле зернятко і відкиньте чорне; Такий процес зменшує кількість зернят у банці. Зрозуміло, що процесс призупиниться, якщо в банці залишиться одне зерно (не можна взяти двох зернят). Чи можна визначити колір зернятка, якщо відома початкова кількість зернят відповідного кольору у банці.
Спроба вирішувати цю задачу, використовуючи тестові приклади з невеликою початковою кількістю зерен в банці, не призводить до якогось результату протягом значного проміжку часу. Цей підхід до вирішення в якомуcь сенсі є аналогом тестування програми з метою виявлення помилок у ній. Знання теорії дозволяє отримати відповідь на питання завдання майже миттєво, проте пояснити це рішення практично неможливо без залучення такого поняття, як інваріант циклу. Інваріант циклу - це предикат, що володіє деякими спеціальними властивостями. Запропонуйте розв’язок цієї задачі. Тепер розглянемо питання про те, наскільки складно протестувати вже написану програму. Будемо припускати для простоти, що для лінійної програми (без розгалужень) достатньо всього одного теста, для програми з одним оператором if - двох (щоб протестувати правильність кожної з його гілок) і так далі. Реальні великі програми, звичайно, не зводяться до сукупності вкладених один в одного умовних операторів. Однак вони не простіші, а складніші - адже в них є і цикли і виклики функцій, підпрограм або методів, обробка виняткових ситуацій та багато іншого. Та все ж, повернемося до нашої моделі. Якщо в програмі 10 операторів if, то потрібно виконати На закінчення поговоримо про правильність великої програми, що складається з багатьох невеликих частин. Припустимо, що для кожної з цих частин ми можемо гарантувати правильність її роботи з імовірністю 99%. Це означає, що в середньому лише в одному випадку зі ста щось може бути не так, а в 99 випадках кожна частина буде працювати абсолютно правильно. Нехай всього таких частин Це - найпростіше завдання з курсу теорії ймовірностей і відповідь така:
При
Лекція 2. АЛГОРИТМИ І ОБЧИСЛЕННЯ Алгоритми Потреби суспільства в узагальненні багатьох підходів до розв’язання різноманітних задач зумовили створення теорії алгоритмів. Бурхливий розвиток науки і техніки в останні століття, спроби філософів найточніше описати різноманітні аспекти людського буття дали світові науку наук – логіку розвитку, яка породжувала задачі, що стимулювали появу нових ідей і методів їх розв’язання. Складність і великий об’єм обчислень зумовили створення спеціалізованих обчислювальних пристроїв. Вони пройшли складний шлях розвитку. Серед них можна виділити один із найпотужніших класів – це електронно-обчислювальні машини (ЕОМ). Проникнення ЕОМ у різні сфери практичної діяльності людей значно вплинуло на еволюцію теорії алгоритмів, на вибір нових напрямів її застосування. Вона перетворилась у певну школу мислення й аналізу для широкого кола програмістів, дала основу мові алгоритмів, яка об’єднує різні напрями досліджень у програмуванні, полегшує розповсюдження ідей. Теорія алгоритмів є важливою частиною прикладної математики, Як відомо, слово алгоритм прийшло з Персії, запропонував його автор книги з математики Abu Jafar Mohammed ibn Musa al Khowarizmi. Він визначав його як деякий спеціальний метод вирішення поставленої проблеми. Поняття алгоритму належить до найскладніших концепцій природознавства. Воно пройшло складний історичний шлях розвитку, починаючи з інтуїтивного розуміння і стихійного застосування на перших кроках розвитку людського суспільства та закінчуючи усвідомленням закономірностей природних явищ, застосуванням у сучасних ЕОМ. Багато авторів визначають розвиток науки як безперервний процес уточнення алгоритмів і побудови відповідних моделей. Умовно можна виділити три основні етапи розвитку теорії алгоритмів. На першому етапі відбувалося накопичення фактів людиною, що засвоювала знання про природу і стихійно формувала та закріплювала власні алгоритми поведінки. Другий етап становлення алгоритмічного апарату пов’язаний з розвитком математичних наук. Для нього є характерним чітке задання математичних алгоритмів розв’язання різних прикладних задач і опис значних алгоритмічних проблем, що не піддавались розв’язанню традиційними методами, наприклад трисекція кута. Третій період бере відлік з початку ХХ ст. Було побудовано формальну класичну теорію алгоритмів, яка уточнювала можливості теоретичного обчислення для практичного застосування в кібернетиці й програмуванні. Теорію алгоритмів можна поділити на класичну і прикладну. У класичній теорії алгоритмів існує безліч формальностей для опису алгоритмів. Серед них можна виділити найзначніші: арифметичне числення предикатів Гьоделя, машини Поста і Тьюринга, автомати Маркова, схеми Янова, блок-схеми. Під алгоритмом розуміють сукупність правил функціонування, що описують поведінку деякої системи, керуючись якими вона досягає кінцевого результату. Алгоритм має скінченну множину кроків, кожен з яких може виконати одну або більше операцій. Операції мають бути однозначними та ефективними. Кожен крок слід виконувати за скінченний, у межах розумного, час. Алгоритм повинен мати хоча б один вихід і нуль або більше зовнішніх входів та закінчуватись після скінченного числа операцій.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 тестів, а якщо їх 20, то вже
тестів, а якщо їх 20, то вже  ! Чи можна сподіватися на те, що в процесі тестування реальної великої програми вдасться перевірити всі можливі варіанти її роботи? Ні, звичайно. Саме тому так важливо не робити помилок, тому що потім їх швидше за все просто не знайти.
! Чи можна сподіватися на те, що в процесі тестування реальної великої програми вдасться перевірити всі можливі варіанти її роботи? Ні, звичайно. Саме тому так важливо не робити помилок, тому що потім їх швидше за все просто не знайти. . Яка ймовірність правильної роботи програми в цілому?
. Яка ймовірність правильної роботи програми в цілому? . Тут -
. Тут -  - імовірність правильної роботи кожної з частин, а
- імовірність правильної роботи кожної з частин, а  - ймовірність правильної роботи програми в цілому. При
- ймовірність правильної роботи програми в цілому. При 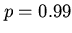 отримуємо результати, наведені в таблиці 7.1.
отримуємо результати, наведені в таблиці 7.1. програма буде працювати правильно трохи більше, ніж в одній третині всіх ситуацій, а при
програма буде працювати правильно трохи більше, ніж в одній третині всіх ситуацій, а при 


